Требования к содержанию программ элективных курсов
Учебное пособие для учащихся
Количество корней квадратного трехчлена
Организационный момент. Сообщение темы и целей занятия
Решение задач. Задание 1 решает один из учеников на доске. Затем ученики выполняют задания самостоятельно с последующей проверкой на доске
Выполнение заданий в парах
При каком значении параметра а корни трехчлена
Закрепление полученных знаний
Организационный момент
Закрепление полученных знаний
Решение отобранных учителем задач из №2 домашнего задания
Проверка уровня знаний, умений и уровня познавательной самостоятельности учащихся
Подведение итогов урока
Навигация
Закрепление полученных знаний
Элективный курс по алгебре для 9-го класса на тему "Квадратные уравнения и неравенства с параметром"
87023
знака
7
таблиц
1
изображение
4. Закрепление полученных знаний.
Совместное решение задач: решение задачи 1 учитель объясняет и записывает на доске, далее – ученики с подсказками учителя.
1. При каких значениях параметра 
неравенство 
выполняется для любых 
2. При каких неравенство 
выполняется для всех 
?
2. При каких значениях неравенство 
выполняется для единственного значения
3. При каких 
неравенства 
и 
равносильны?
4. При каких значениях параметра с все значения функции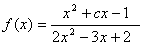 
принадлежат интервалу 
5. При каких функция 
определена для всех ?
5. Подведение итогов занятия.
- Сложно ли было найти идею для решения той или иной задачи?
- Интереснее решать задания по определенному алгоритму (иногда приводящему к длинному решению и громоздким вычислениям) или в каждой задаче искать свой, более рациональный, путь решения?
Учитель оценивает работу учащихся на занятии по пятибалльной шкале и сообщает результаты. Ученики могут повысить или понизить оценку друг друга, аргументировав свой ответ.
6. Постановка домашнего задания.
Домашнее задание дается по вариантам. Его учащиеся выполняют за день до следующего занятия и отдают на проверку одноклассникам: те, у кого был первый вариант, проверяют задания у тех, у кого был второй вариант.
Вариант 1.
1. При каких значениях график функции
2. 
целиком расположен ниже оси абсцисс? Ответ: 
.
2. При каких неравенство 
выполняется только для одного значения Ответ: 
3. При каких значениях прямая 
не пересекает параболы 
и 
? Ответ: 
Вариант 2.
1. При каких значениях неравенство 
выполняется для любых Ответ: 
2. При каких значениях функция 
принимает только отрицательные значения? Ответ: 
.
3. При каких значениях и 
прямая 
имеет с каждой параболой и единственную общую точку? Ответ: 
и 
.
Литература: [20], [25].
Занятие VI. Расположение корней квадратного уравнения
Цель: рассмотрение условий, определяющих расположение корней квадратного уравнения; закрепление имеющихся знаний.
Ход занятия:
1. Организационный момент. Сообщение плана и цели занятия.
2. Проверка домашнего задания. Задания, вызвавшие наибольшие затруднения, разбираются. Их решение объясняют ученики, которые справились с заданием.
3. Лекция по теме «Расположение корней квадратного уравнения» (Приложение 1).
4. Подведение итогов занятия.
- С чем сегодня познакомились на уроке? Какие новые факты узнали?
5. Постановка домашнего задания.
1. При каких значениях параметра а корни уравнения 
меньше 1?
2. Найти множество значений параметра m , при котором уравнение 
имеет два корня, заключенные между -1 и 1.
3. При каких значениях параметра а уравнение 
имеет хотя бы один общий корень с уравнением 
?
Литература: [2], [7], [9], [13], [17], [25], [32], [33].
Занятие VII. Расположение корней квадратного трехчлена
Цель: закрепление знаний по теме «Расположение корней квадратного уравнения».
Ход занятия:
Похожие работы
... -иллюстративного и репродуктивного метолов, а экономический профиль ориентирован на формирование прикладного стиля мышления. 2. Методика проведения элективных курсов по математике в профильной школе 2.1 Цели организации элективных курсов по математике Принципиальным положением организации школьного математического образования в настоящее время является дифференциация обучения ...
... на уроках алгебры и занятиях элективного курса по математике, участие проектной группы в городской конференции по данной теме в 2006 году. Объектом исследовательской работы было решение уравнений с параметрами, связанных со свойствами выше представленных функций. Структура данной работы включает в себя теорию, практическую часть, заключение, библиографический список. Решение уравнений с ...
... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9. Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...
... Этим числам соответствуют три точки: A (), B () и C (). Они расположены на единичной окружности и делят ее на три равные части (рис. 18). Рис. 18. Задача 42. Изобразите на плоскости комплексные числа , удовлетворяющие условию: . Решение , значит, и . Получили две точки: B () и C () (рис. 19). Рис. 19. Задача 43. Изобразите множество точек комплексной плоскости, удовлетворяющих условию: ...
0 комментариев