Стандартні ірраціональні рівняння

2. Стандартні ірраціональні рівняння

Як правило, у шкільному курсі розгляд ірраціональних рівнянь зводиться до розбору декількох нескладних прикладів. Вони в більшості випадків вирішуються введенням у квадрат лівої й правої частин рівняння. Після рішення обов'язково виконується перевірка. Не звертається увага на те, що ірраціональні рівняння можуть вирішуватися й з використанням поняття рівносиль. У даному параграфі представлені різні види ірраціональних рівнянь, які можна віднести до стандартного й вирішувати одним з наступних методів, а саме:

1) метод переходу до рівняння - наслідку з наступною перевіркою отриманих корінь;

2) метод рівносильного переходу до рівняння або до змішаної системи;

3) метод введення нової змінної.

2.1 Рівняння виду

 

Приклад 1. Вирішити рівняння .

Рішення. Зведемо обидві частини вихідного рівняння у квадрат..

Відповідь: {6}.

Приклад 2. Вирішити рівняння .

Рішення. У лівій частині вихідного рівняння коштує арифметичний квадратний корінь - він по визначенню ненегативний, а в правій частині - негативне число.

Отже, рівняння не має кореня.

Відповідь: .

Запишемо рівносиль, за допомогою якої вирішуються рівняння даного виду.

 , якщо  й не має рішення, якщо .

Приклад 3. Вирішити рівняння .

Рішення. Зведемо обидві частини вихідного рівняння в куб.

; .

Відповідь: {-5}.

Запишемо рівносиль, за допомогою якої вирішуються рівняння даного виду: .

2.2 Рівняння виду

Досить часто при рішенні рівнянь даного виду учні використовують наступне формулювання властивості добутку «Добуток двох співмножників дорівнює нулю, коли хоча б один з них дорівнює нулю». Помітимо, що формулювання властивості добутку повинна виглядати в такий спосіб: « добуток двох співмножників дорівнює нулю, коли хоча б один з них дорівнює нулю, а іншої при цьому має сенс».

Запишемо рівносиль, за допомогою якої вирішуються рівняння даного виду:

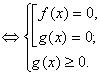
Приклад 1. Вирішити рівняння .

Рішення.

.

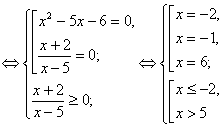Відповідь: {-2;6}.

Приклад 2. Вирішити рівняння .

Рішення. У цьому випадку рівняння не має виду, зазначеного в заголовку. Отже, його необхідно перетворити. Але спочатку знайдемо ОПЗ змінної .

ОПЗ: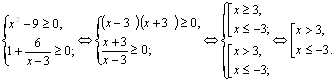

Перетворимо рівняння до виду

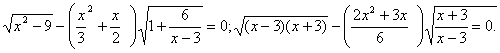
При рішенні рівняння учні часто необґрунтовано ділять обидві частини рівняння на вираження, що містить невідоме (у цьому випадку, на ), що приводить до втрати кореня й придбанню «стороннього». Подібні рівняння, що містять в обох частинах загальний множник, варто вирішувати переносом всіх членів в одну частину й розкладанням отриманого вираження на множники.

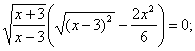
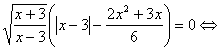
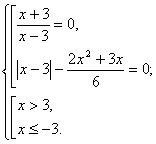
Вирішимо кожне рівняння із сукупності.

; .

(1).

З огляду на, що ОПЗ:  одержуємо, що рівняння (1) рівно сильно сукупності:

. Тоді ,  не задовольняє умові

, дане рівняння не має корінь.

Отже, сукупність прийме наступний вид:

Повернемося до системи:

Відповідь: {-3;6}.

2.3 Ірраціональні рівняння, які вирішуються введенням нової змінної

При рішенні різних видів рівнянь: раціональних, тригонометричних, показових часто використовується метод введення нової змінної. Нова змінна в рівняннях іноді дійсно очевидна, але іноді її важко побачити, а можна виявити тільки лише в процесі яких або перетворень. Буває корисно ввести не одну, а дві змінні. Бачимо типові випадки введення нових змінних в ірраціональних рівняннях.

Приклад 1. Вирішити рівняння

Рішення. Уведемо нову змінну. Нехай , , де . Одержуємо, що  .Тоді - не задовольняє умові

Виконаємо зворотну заміну.

Відповідь:{34}.

Приклад 2. Вирішити рівняння

Рішення. Самота радикала й введення в ступінь обох частин рівняння привело б до громіздкого рівняння. У той же час, якщо виявити деяку спостережливість, то можна помітити, що дане рівняння зводитися до квадратного. Дійсно, помножимо обидві частини заданого рівняння на 2, одержимо, що    

Уведемо нову змінну. Нехай  Одержуємо, що . Тоді  - не задовольняє умові ,

Виконаємо зворотну заміну.   Тоді ,

Так як вихідне рівняння рівносильне рівнянню  те перевірка отриманих корінь не потрібна.

Відповідь: {-2;3,5}.

Приклад 3. Вирішити рівняння

Рішення. Перетворимо дане рівняння.

Уведемо нову змінну. Нехай,  а  Одержуємо, що . Тоді - не задовольняє умові .

Виконаємо зворотну заміну. .

2.4 Рівняння виду , ,

Дані рівняння можна вирішити за допомогою основного методу рішення ірраціональних рівнянь (введення у квадрат обох частин рівняння), але іноді їх можна вирішити й іншими методами.

Розглянемо рівняння  (1). Нехай  - корінь рівняння (1). Тоді справедливо числова рівність . Знайдемо різницю чисел  і , позначивши її , і запишемо дану рівність у вигляді  (2).

Використовуючи, що , запишемо рівність (2) у вигляді . Дана рівність означає, що число  є корінь рівняння  (3).

Таким чином, рівняння (3) є наслідком рівняння (1). Складаючи ці два рівняння й множачи отримане рівняння на а, одержимо рівняння (4), що також є наслідком рівняння (1). Звівши рівняння (4) у квадрат і вирішивши отримане рівняння, потрібне виконати перевірку знайдених корінь, тобто перевірити, чи є його коріння коріннями рівняння (1).

Зауваження. Відзначимо, що точно також доводиться, що рівняння (4) є наслідок рівняння .

Приклад 1. Вирішити рівняння  (5).

Рішення. Різниця підкореневих виражень  і  є

. ,

те рівняння (6) є наслідком вихідного рівняння. Тоді, складаючи рівняння (5) і (6), одержимо рівняння  (7), що також є наслідком вихідного рівняння (5). Зведемо обидві частини рівняння (6) у квадрат, одержимо рівняння  (8), що також є наслідком вихідного рівняння. Вирішуючи рівняння (8), одержуємо, що ,

Перевіркою переконуємося, що обоє цих числа є коріннями вихідного рівняння.

Відповідь: .

Зауваження. Рівняння виду  можна вирішувати множенням обох частин рівняння на деяке вираження, що не приймає значення нуль (на сполучене лівій частині рівняння тобто

Приклад 2. Вирішити рівняння  (8).

Рішення. , те помножимо обидві частини рівняння на вираження , що є сполученим лівої частини рівняння (8).  . Після приведення подібних доданків одержуємо рівняння  (9), рівносильне вихідному, тому що рівняння дійсних корінь не має. Складаючи рівняння (8) і (9) одержуємо, що . Тоді

Відповідь: .

Зауваження. Також рівняння виду  можна вирішувати за допомогою ОПЗ рівняння й рівносильних переходів від одних рівнянь до інших.

Приклад 3. Вирішити рівняння

Рішення. Знайдемо ОПЗ змінної х.

ОПЗ: Отже,

На ОПЗ обидві частини рівняння позитивні, тому після введення у квадрат одержимо рівняння: , рівносильне для  рівнянню

Іноді рішення рівняння можна знайти, вирішуючи його на різних числових проміжках.

Для кожного маємо , а . Отже, серед немає рішень рівняння .

Для  маємо . Отже,  для . . Тоді . Так як , те  є коренем рівняння , рівносильному рівнянню  для цих х.

Відповідь: .

Приклад 4. Вирішити рівняння

Рішення. Перетворимо вихідне рівняння.

Зведемо обидві частини даного рівняння у квадрат.

Перевірка показує, що 5 є коренем вихідного рівняння.

Зауваження. Іноді значно простіше можна вирішувати рівняння виду , якщо скористатися властивостями монотонності функцій, а саме тим, що сума двох зростаючих функцій є зростаючою функцією, і всяка монотонна функція кожне своє значення приймає, лише при одному значенні аргументу. Дійсно, функції  й - зростаючі. Отже, їхня сума - зростаюча функція.

Виходить, вихідне рівняння, якщо має корінь, те тільки один. У цьому випадку, з огляду на, що , підбором легко знайти, що 5 є коренем вихідного рівняння.

Приклад 5. Вирішити рівняння

Рішення. Якщо обидві частини вихідного рівняння піднести до квадрата, то вийде досить складне рівняння. Надійдемо по-іншому: перетворимо рівняння до виду:

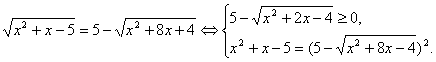
Вирішимо нерівність системи.

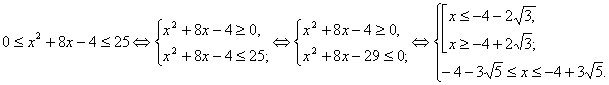
Рішенням системи є множина:

.

Вирішимо рівняння системи.

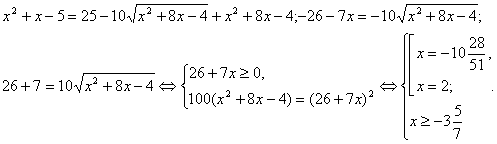
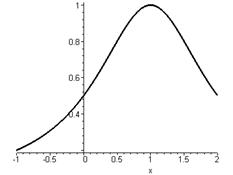
Переконуємося, що 2 належить множині рішень нерівності (мал.1).

Зауваження. Якщо вирішувати дане рівняння введенням обох частин у квадрат, то необхідно виконати перевірку. 2 - ціле число, тому при виконанні перевірки труднощів не виникають. А що стосується значення , то підстановка його у вихідне рівняння приводить до досить складних обчислень. Однак такої підстановки можна уникнути, якщо помітити, що при цьому значенні права частина рівняння  приймає негативне значення: . Тоді як ліва частина рівняння негативної бути не може. Таким чином, не є коренем рівняння - наслідку даного рівняння. Тим більше, це значення не може бути коренем вихідного рівняння. Отже, корінь рівняння - число 2.

Приклад 6. Вирішити рівняння

Рішення. Знайдемо ОПЗ змінної х.

ОПЗ: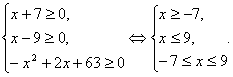  

Отже,

Для будь-яких значень  із ОПЗ, що задовольняють умові , тобто для  із проміжку  ліва частина рівняння негативна, а перша – ненегативна, виходить, жодне із цих  рішенням рівняння бути не може.

Нехай . Для таких  обидві частини рівняння ненегативні, і тому воно рівносильне на цій множині рівнянню:

.

Уведемо нову змінну. . Одержуємо, що . Тоді  - не задовольняє умові , .

Виконаємо зворотну заміну.

; ;

.

Тоді - не задовольняє умові ,

Відповідь: .

Приклад 7. Вирішити рівняння

Рішення. Знайдемо ОПЗ змінної х.

ОПЗ: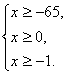  

Отже, що

Легко бачити, що , тому що .

Розділимо обидві частини рівняння на . Одержуємо, що

Перетворимо . Уведемо нову змінну. Нехай , а . Тоді рівняння прийме вид: ; ; : . Тоді - не задовольняє умові , . Виконаємо зворотну заміну.

Відповідь: .

Приклад 8. Вирішити рівняння

Рішення. Перетворимо вихідне рівняння.

Зведемо обидві частини отриманого рівняння у квадрат.

 

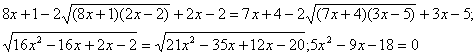
Тоді

Отже, перевірка показує, що -1,2 - не є коренем вихідного рівняння, а 3 - є.

Зауваження. Дане рівняння можна вирішувати й за допомогою рівносильних переходів, але тоді його рішенні буде набагато складніше, ніж наведене вище.

Відповідь: {3}.

Приклад 9. Вирішити рівняння

Рішення. Помітимо, що всі квадратні тричлени позитивні відносно  . Перепишемо рівняння у вигляді:

Позначимо для стислості підкореневі вираження через  відповідно. Помножимо й розділимо ліву й праву частину рівняння на сполучені співмножники. Одержуємо, що

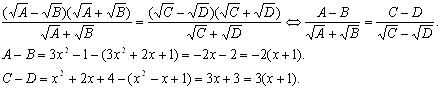
Повернемося до рівняння.

Друге рівняння сукупності рішень не має, оскільки обидва знаменники позитивні. Отже,

Зауваження. Також рішення даного рівняння можна знайти, досліджуючи його на різних числових проміжках.

Спочатку виділимо  й  відповідно в кожному з підкореневих виражень у правій частині рівняння.

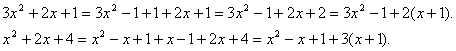
Отже, вихідне рівняння має вигляд:

Позначимо для стислості підкореневі вираження через , ,  і  відповідно. Так як вираження  звертається в нуль при , те розглянемо рішення даного рівняння при ,  і .

Якщо , то > , > + > + .

Отже, при  вихідне рівняння не має корінь.

Якщо , то < , < + < + .

Отже, при  вихідне рівняння не має корінь.

Якщо , то = , = + = + .

Отже, -1 є єдиним коренем вихідного рівняння.

Відповідь:{-1}.

Зауваження. Отже, при рішенні рівнянь із радикалами потрібне вміти користуватися кожним із цих методів і вибирати в кожному випадку оптимальний.

3. Не стандартні методи рішення ірраціональних рівнянь

Існують ірраціональні рівняння, які вважаються для школярів звичайних освітніх шкіл задачами підвищених труднощів. Для рішення таких рівнянь краще застосовувати не традиційні методи, а прийоми, які не зовсім звичні для учнів. У цій главі приводяться рішення рівнянь заснованих на графічних міркувань, властивостях функції (таких, як монотонність, обмеженість, парність), застосуванні похідній і т.д.