Змішані ірраціональні рівняння й методи їхнього рішення

4. Змішані ірраціональні рівняння й методи їхнього рішення

 

4.1 Ірраціональні рівняння, що містять подвійну ірраціональність

Приклад 1. Вирішити рівняння

Рішення. Зведемо обидві частини рівняння в куб.

 Зведемо обидві частини отриманого рівняння у квадрат.

Уведемо нову змінну. Нехай , тоді . Одержуємо, що . Тоді .

Виконаємо зворотну заміну.  Або .

Тоді  або

Перевірка показує, що  не є коренем даного рівняння, а 1- є.

Відповідь: {1}.

Приклад 2. Вирішити рівняння

Рішення.

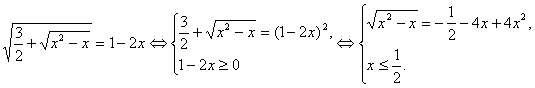
Уведемо нову змінну. Нехай . Тоді

Тоді система прийме наступний вид:

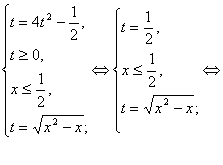
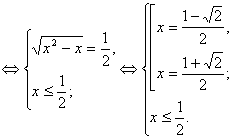
Відповідь: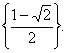

Приклад 3. Вирішити рівняння

Рішення. Уведемо нову змінну. Нехай . Тоді . Одержуємо, що

.

Так як. , те дане рівняння рівносильне наступний:

Одержуємо, що . З огляду на, що , те рішення: . Отже, .

Виконаємо зворотну заміну. . Тоді

Відповідь: [-4;0].

Приклад 4. Вирішити рівняння

Рішення. Перетворимо підкореневі вираження.

Повернемося до вихідного рівняння.

Останнє рівняння вирішимо методом інтервалів.

Нехай . Одержуємо, що

. , те на даному проміжку рівняння не має корінь.

Нехай . Одержуємо, що Рівність вірно. Знайдемо всі значення  з даного проміжку.. Отже,

Нехай . Одержуємо, що . Так як , те на даному проміжку рівняння не має корінь.

Зауваження. Дане рівняння можна вирішувати, виконавши заміну змінної . Після рішення вихідного рівняння щодо змінної , виконавши зворотну заміну, знайдемо корінь рівняння.

Відповідь: [0;3].

Зауваження. Вираження виду  звичайно називають подвійним радикалом або складним радикалом.

Якщо підкореневе вираження являє собою повний квадрат, то можна в подвійному радикалі звільнитися від зовнішнього радикала, скориставшись рівністю .

Перетворення подвійних радикалів.

Вправа 1. Звільнитися від зовнішнього радикала у вираженні .

Рішення. Доданок  можна розглядати як подвоєний добуток чисел  і  або чисел  і . Число 7 повинне бути дорівнює сумі квадратів цих чисел. Підбором знаходимо, що ця умова виконується для чисел  і , тобто .

Одержуємо, що

Відповідь: .

4.2 Ірраціональні показові рівняння

Приклад 1. Вирішити рівняння .

Рішення. ;  - рішень немає.

Відповідь:

Приклад 2. Вирішити рівняння

Рішення.

  

- Рішень ні, тому що

Відповідь:

Приклад 3. Вирішити рівняння

;

Відповідь: .

Примі 4. Вирішити рівняння

Рішення.

;

Уведемо нову змінну. Нехай . Одержуємо, що . Тоді

Виконаємо зворотну заміну.  Або

;

- рішень немає.

; .

Відповідь:{3}.

Приклад 5. Вирішити рівняння

Рішення. Множина М – загальна частина (перетинання) областей існування функцій - є всі

На множині М функції  й  позитивні. Тому, логарифмуючи обидві частини рівняння, одержимо рівняння, рівносильне вихідному на М.

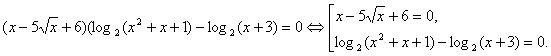
Вирішимо рівняння сукупності.

. Уведемо нову змінну. Нехай . Одержуємо, що . Тоді . Виконаємо зворотну заміну.  або . Тоді  або .

Одержуємо, що вихідне рівняння рівносильне системі:

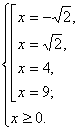
Відповідь: .

Зауваження. У задачах підвищеної складності зустрічаються рівняння виду , де - деякі позитивні числа. Такі рівняння не є ірраціональними рівняннями, тому що не містять змінної під знаком радикала, але всі, же розберемо їхнє рішення в даному пункті.

Приклад 6. Вирішити рівняння

Рішення. Перетворимо вираження

Тоді вихідне рівняння прийме вид:

Зауваження. Можна помітити, що , отже,  і - взаємно обернені числа. Тоді . Уведемо нову змінну. Нехай , а Одержуємо, що вихідне рівняння рівносильне наступний . Тоді

Виконаємо зворотну заміну.

 або

; ;

Тоді .

;

Тоді

Відповідь :{-2;2}.

4.3 Ірраціональні логарифмічні рівняння

Приклад 1. Вирішити рівняння

Рішення. ;

З огляду на, що , дане рівняння рівносильне системі:

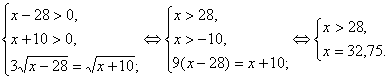
Відповідь:{32,75}.

Приклад 2. Вирішити рівняння

Рішення. . Перетворимо праву частину рівняння.

Повернемося до вихідного рівняння.

;

Уведемо нову змінну. Нехай . Одержуємо, що

.

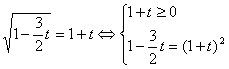Вирішимо рівняння системи.

; .

Тоді

Повернемося до системи: 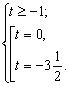Отже,

Виконаємо зворотну заміну:

Перевірка показує, що 1 є коренем вихідного рівняння.

Відповідь: {1}.

Приклад 3. вирішити рівняння

Рішення. Знайдемо ОПЗ змінної х.

ОПЗ:

.

На ОПЗ вихідне рівняння рівносильне рівнянню

; ;

Уведемо нову змінну. Нехай  або

;

;

Відповідь: {3;81}.

Висновок

Дана курсова робота допомогла мені навчитися вирішувати ірраціональні рівняння наступних типів: стандартного, нестандартного, показового, логарифмічні, підвищеного рівня. Застосовувати основні властивості функції, область визначення, область значення функції. Використовувати найбільше й найменше значення функції. Застосування похідної. Я вважаю, що цілі які поставлені перед виконанням курсової роботи виконані.

Література

1. Харкова О.В. Ірраціональні рівняння. – К., 2004

2. Колмогоров О.М. Алгебра й початок аналізу. – К., 2003

3. Куланін Е.Д., Норін В.П. 3000 конкурсних задач по математиці. – К., 2000

4. Гусєв В.А., Мордкович А.Д. Довідкові матеріали по математиці. – К., 2003

5. Сканаві М.М. Збірник задач по математиці. – К., 2006