Навигация
Застосування основних властивостей функції
33467
знаков
0
таблиц
4
изображения
3.1 Застосування основних властивостей функції
3.1.1 Використання області визначення рівняння
Іноді знання області визначення рівняння дозволяє довести, що рівняння не має рішень, а іноді дозволяє знайти рішення рівняння безпосередньою підстановкою чисел з її.
Приклад 1. Вирішити рівняння 
.
Рішення. Знайдемо область визначення рівняння.
ОПЗ: 
.
Отже, дана система рішень не має.
Так як система рішень не має, то й дане рівняння не має корінь.
Відповідь: 
.
Приклад 2. Вирішити рівняння 
Рішення. Знайдемо ОПЗ змінної х.
ОПЗ: 
.
Отже, 
або 
.
Таким чином, рішення даного рівняння можуть перебувати серед знайдених двох чисел.
Перевіркою переконуємося, що тільки 2 є коренем вихідного рівняння.
Відповідь: {2}.
3.1.2 Використання області значень рівнянь
Приклад 1. Вирішити рівняння 
Рішення.. 
, отже, 
, але 
(права частина рівняння негативна, а ліва позитивна), значить дане рівняння не має рішень.
Відповідь: 
Приклад 2. Вирішити рівняння 
.
Рішення. 
, те
; 
; 
; 
; 
; 
; 
.
Отже, ліва частина рівняння приймає ненегативне значення тільки при . А це значить, що його коренем може бути тільки значення 5, а може трапитися, що рівняння взагалі не буде мати корінь. Для рішення цього питання виконаємо перевірку.
Перевірка показує, що 5 є коренем вихідного рівняння.
Відповідь: {5}.
3.1.3 Використання монотонності функції
Рішення рівнянь і нерівностей з використанням властивостей монотонності ґрунтується на наступних твердженнях.
1. Нехай f(x) - безперервна й строго монотонна функція на проміжку Q, тоді рівняння f(x)=c, де c - дана константа може мати не більше одного рішення на проміжку Q.
2. Нехай f(x) і g(x) - безперервні на проміжку Q функції, f(x) - строго зростає, а g(x)- строго убуває на цьому проміжку, тоді рівняння f(x)= g(x) може мати не більше одного рішення на проміжку Q.
Відзначимо, що в кожному з випадків проміжки Q можуть мати один з видів: 
Приклад 1. Вирішимо рівняння 
Рішення. Знайдемо ОПЗ змінної х.
ОПЗ: 
.
Отже, 
.
На ОПЗ функції 
й 
безперервні й строго убувають, отже, безперервна й убуває функція 
. Тому кожне своє значення функція h(x) приймає тільки в одній крапці. Так як h(2)=2 , те 2 є єдиним коренем вихідного рівняння.
Відповідь: {2}.
3.1.4 Використання обмеженості функції
Якщо при рішенні рівняння 
вдається показати, що для всіх 
з деякої множини М справедливі нерівності 
й 
, то на множині М рівняння рівносильне системі рівнянь: 
.
Приклад 1. Вирішити рівняння 
.
Рішення. Функції, що коштують у різних частинах рівняння, визначені на 
. Для кожного 
. Отже, дане рівняння рівносильне системі рівнянь
.
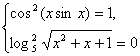Вирішимо друге рівняння системи:
; 
; 
Тоді 
Перевірка показує, що 0 є коренем даного рівняння, а - 1-не є.
Відповідь:{0}.
Приклад 2. Вирішити рівняння 
Рішення. Оцінимо підкореневі вираження.
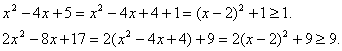
Отже, 
, 
Так як перший доданок лівої частини вихідного рівняння обмежено знизу одиницею, а другий доданок-3, те їхня сума обмежена знизу 4. Тоді ліва частина рівняння стає рівної правої частини рівняння при .
Відповідь:{2}.
Похожие работы
... анализ управленческих функций: Пер. с англ. – М.: прогресс, 1981. 6. Мескон А., Альберт М., Хедоури Ф. Основы менеджмента: Пер с англ. – М.: Дело. 1992. 7. Планкетт Л., Хейл Г. Выработка и принятие управленческих решений: опережающее управление: Пер. с англ. – М: Экономика, 1984. 8. Труханов Р.И. Модели принятия решений в условиях неопределенности. – М.: Наука, 1991. 9. Фалм
і дані завдань варіанту №7 1. Завдання №1 1.1 Задача 1.1 (вар. №7) Спростити вираз Розв’язання. Алгебраїчні перетворення в Maple проводяться за допомогою вбудованих функцій елементарних перетворень таких як simplify - спростити, expand - розкрити дужки, factor -розкласти на множники, normal - привести до спільного знаменника, combine-перетворення ступеня, collect- ...
... з відсутністю творчого підходу до розв’язування задач, невмінням логічно мислити, синтезувати при розв’язанні проблемних задач різноманітні розділи математики – алгебру, геометрію і тригонометрію. Використання ЕОМ для опрацювання результатів контролю знань потребує одержання числової відповіді в задачі. Це скорочує можливі помилки операторів при введенні цих результатів у пам’ять ЕОМ. Тому у ...
... раціоналізм античної науки не може бути адекватно і цілісно зрозумілим і відображеним без системного аналізу основ і теоретичної еволюції античної математики. · У процесі відродження античної думки (у ренесансній філософії), її критичної переробки, у методології раціоналізму Нового часу відбулася втрата частини семантичного змісту і змісту теоретичного раціоналізму античної філософії і ...
0 комментариев