Навигация
1.2 Вычисление интегралов
Рассмотрим функцию 
, заданную на интервале 
, требуется приближенно вычислить интеграл
(2.1)
Этот интеграл может быть несобственным, но абсолютно сходящимся.
Выберем произвольную плотность распределения 
, определённую на интервале 
. Наряду со случайной величиной 
, определённой в интервале с плотностью , необходимо определить случайную величину
Согласно соотношению 
получим
Рассмотрим теперь 
одинаковых независимых случайных величин 
и применим к их сумме центральную предельную теорему. Формула (1.7) в этом случае запишется так:
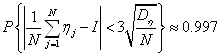
Последнее соотношение означает, что если выбирать значений 
, то при достаточно большом
(2.2)
Оно показывает также, что с очень большой вероятностью погрешность приближения (2.2) не превосходит 
.
Для расчёта интеграла (2.1) можно использовать любую случайную величину . Определённую в интервале с плотностью 
. В любом случае 
. Однако дисперсия 
, а с ней и оценка погрешности формулы (2.2) зависят от того, какая величина используется, так как
(2.3)
Докажем, что это выражение будет минимальным тогда, когда пропорциональна 
.
Для этого воспользуемся неравенством
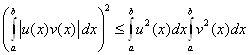, в которым положим 
, 
. Получим неравенство
(2.4)
Из (2.3), (2.4) следует, что
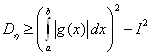(2.5)
Остается доказать, что нижняя граница дисперсии (2.5) реализуется при выборе плотности 
. Так как
.
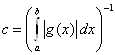Следовательно,
,
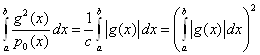и правая часть (2.3) обращается в правую часть (2.5)
Использовать плотность 
для расчёта практически невозможно, так как для этого нужно знать значение интеграла 
. А его вычисление представляет собой задачу, равноценную задаче о вычислении интеграла (2.1). Поэтому ограничиваются следующей рекомендацией: желательно, чтобы плотность была пропорциональна .
Конечно, выбирать очень сложные нельзя, так как процедуры разыгрывания станет очень трудоёмкой. Оценку (2.2) с плотностью , сходной , называют существенной выборкой.
Также если стоит задача вычислить интеграл (2.1), преобразуем его к виду
(2.6)
Если теперь обозначить 
(2.7)
То интеграл принимает вид
(2.8)
и может быть вычислен при помощи метода статистических испытаний.
В частном случае, если 
и 
конечны или их можно считать конечными приближенно, в качестве 
целесообразно выбрать равномерный закон распределения.
Как известно, плотность вероятности равномерного закона распределения в интервале равна:
(2.9)
Подставим в интеграл (2.6) значение из формулы (2.9) и получим:
(2.10)
и рассмотрим процедуру вычисления:
из множества равномерно распределённых случайных чисел выбирается 
. Для каждого значения вычисляется 
, затем вычисляется среднее значение
(2.11)
функции на интервале
Таким образом, величина интеграла (2.10) может быть представлена в виде следующей формулы
(2.12)
Рассмотренный частный случай находит широкое применение интегралов методом статистического моделирования в силу того, что границы области определения могут быть легко приведены к пределам интегрирования
Похожие работы
... частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*. §2. Оценка погрешности метода Монте-Карло. Пусть для получения оценки a* математического ожидания а случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х) ...
... в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для исследования различного рода сложных систем (автоматического управления, экономических, биологических и т.д.). Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой а: (1) ...
етка – одно из простейших средств получения случайных чисел с хорошим равномерным распределением, на использовании которых основан этот метод. Метод Монте – Карло это статистический метод. Его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, в теориях передачи информации, при исследовании сложных ...
... опыт», учится на своих и чужих ошибках и постепенно выучиваться принимать правильные решения – если не оптимальные, то почти оптимальные. Попробуем проиллюстрировать процесс имитационного моделирования через сравнение с классической математической моделью. Этапы процесса построения математической модели сложной системы: 1. Формулируются основные вопросы о поведении ...
0 комментариев