Навигация
2. Практическая часть
2.1 Пример 1
Вычислим приближенно интеграл 
Точное значение его известно: 
Используем для вычисления две различные случайные величины 
, с постоянной плотностью 
(т.е. равномерна распределена в интервале 
) и с линейной плотностью 
.Линейная плотность более соответствует рекомендации о пропорциональности 
и 
. Поэтому следует ожидать, что второй способ вычисления даст лучший результат.
1) Пусть , формула для разыгрывания имеет вид 
. А формула (2.2) примет вид 
.
Пусть 
. В качестве значений 
используем тройки чисел из табл. 1 (см. приложение), умноженные на 0.001. Промежуточные результаты сведены в табл. 2.1. Результат расчёта 
Таблица 2.1
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
| 0.865 | 0.159 | 0.079 | 0.566 | 0.155 | 0.664 | 0.345 | 0.655 | 0.812 | 0.332 |
|
| 1.359 | 0.250 | 0.124 | 0.889 | 0.243 | 1.043 | 0.542 | 1.029 | 1.275 | 0.521 |
|
| 0.978 | 0.247 | 0.124 | 0.776 | 0.241 | 0.864 | 0.516 | 0.857 | 0.957 | 0.498 |
2) пусть теперь . Для разыгрывания используем формулу
,
откуда получаем
формула (2.2) имеет вид
Пусть . Числа выберем те же, что и в случае 1. Промежуточные результаты сведены в табл. 2.2. Результат расчёта 
Таблица 2.2
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
| 0.865 | 0.159 | 0.079 | 0.566 | 0.155 | 0.664 | 0.345 | 0.655 | 0.812 | 0.332 |
|
| 1.461 | 0.626 | 0.442 | 1.182 | 0.618 | 1.280 | 0.923 | 1.271 | 1.415 | 0.905 |
|
| 0.680 | 0.936 | 0.968 | 0.783 | 0.937 | 0.748 | 0.863 | 0.751 | 0.698 | 0.868 |
Как и ожидалось, второй способ вычислений дал более точный результат.
3) По значениям, приведённым в таблицах (2.1) и (2.2) можно приближенно сосчитать дисперсии 
для обоих методов расчёта:
для 1:
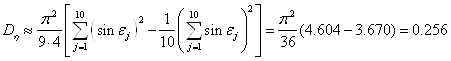
для 2:
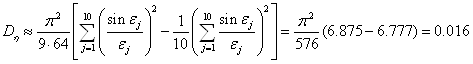
Несмотря на то, что значение невелико и приближенная нормальность оценки (2.2) не гарантирована, вычислим для обоих методов величины 
. Получим значения 0.103 и 0.027. Также фактические абсолютные погрешности при расчёте 
, равные 0.048 и 0.016, – величины того же порядка. Точные же значения в рассмотренном примере равны 0.233 и 0.0166. Таким образом, и при оценке дисперсий метод 2 оказался точнее метода 1.
Похожие работы
... частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*. §2. Оценка погрешности метода Монте-Карло. Пусть для получения оценки a* математического ожидания а случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х) ...
... в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для исследования различного рода сложных систем (автоматического управления, экономических, биологических и т.д.). Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой а: (1) ...
етка – одно из простейших средств получения случайных чисел с хорошим равномерным распределением, на использовании которых основан этот метод. Метод Монте – Карло это статистический метод. Его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, в теориях передачи информации, при исследовании сложных ...
... опыт», учится на своих и чужих ошибках и постепенно выучиваться принимать правильные решения – если не оптимальные, то почти оптимальные. Попробуем проиллюстрировать процесс имитационного моделирования через сравнение с классической математической моделью. Этапы процесса построения математической модели сложной системы: 1. Формулируются основные вопросы о поведении ...
0 комментариев