Навигация
Вычисление кратных интегралов
1.3 Вычисление кратных интегралов
Обычно при вычислении кратных интегралов методом Монте-Карло используют один из двух способов.
Первый способ.
Пусть требуется вычислить ![]() кратный интеграл
кратный интеграл
![]() (3.1)
(3.1)
по области G, лежащей в ![]() мерном единичном кубе
мерном единичном кубе
![]()
![]()
Выберем ![]() равномерно распределённых на отрезке
равномерно распределённых на отрезке ![]() последовательностей случайных чисел
последовательностей случайных чисел
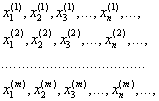
Тогда точки ![]() можно рассматривать как случайные, равномерно распределённые в
можно рассматривать как случайные, равномерно распределённые в ![]() мерном единичном кубе.
мерном единичном кубе.
Пусть из общего числа ![]() случайных точек
случайных точек ![]() точек попали в область G, остальные
точек попали в область G, остальные ![]() оказались вне G. Тогда при достаточно большом
оказались вне G. Тогда при достаточно большом ![]() имеет место приближенная формула:
имеет место приближенная формула:
![]() (3.2)
(3.2)
где под ![]() понимается
понимается ![]() мерный объём области интегрирования. Если вычисление объёма
мерный объём области интегрирования. Если вычисление объёма ![]() затруднительно, то можно принять
затруднительно, то можно принять ![]() , и для приближенного вычисления интеграла получим:
, и для приближенного вычисления интеграла получим:
![]() (3.3)
(3.3)
Указанный способ можно применить к вычислению кратных интегралов и для произвольной области ![]() , если существует такая замена переменных, при которой новая область интегрирования будет заключена в
, если существует такая замена переменных, при которой новая область интегрирования будет заключена в ![]() мерном единичном кубе.
мерном единичном кубе.
Второй способ.
Если функция ![]() , то интеграл (3.1) можно рассматривать как объём тела в
, то интеграл (3.1) можно рассматривать как объём тела в ![]() мерном пространстве, т.е.
мерном пространстве, т.е.
![]() (3.5)
(3.5)
где область интегрирования ![]() определяется условиями
определяется условиями ![]()
Если в области ![]()
![]() , то введя новую переменную
, то введя новую переменную ![]() , получим
, получим
![]()
где область ![]() лежит в единичном
лежит в единичном ![]() мерном кубе
мерном кубе ![]()
Возьмём ![]() равномерно распределенных на отрезке
равномерно распределенных на отрезке ![]() случайных последовательностей
случайных последовательностей
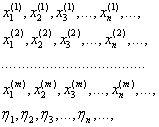
Составим соответствующую последовательность случайных точек ![]()
Пусть из общего числа ![]() случайных точек
случайных точек ![]() точек принадлежат объёму
точек принадлежат объёму ![]() , тогда имеет место приближенная формула
, тогда имеет место приближенная формула
![]() (3.6)
(3.6)
Похожие работы
... частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*. §2. Оценка погрешности метода Монте-Карло. Пусть для получения оценки a* математического ожидания а случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х) ...
... в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для исследования различного рода сложных систем (автоматического управления, экономических, биологических и т.д.). Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой а: (1) ...
етка – одно из простейших средств получения случайных чисел с хорошим равномерным распределением, на использовании которых основан этот метод. Метод Монте – Карло это статистический метод. Его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, в теориях передачи информации, при исследовании сложных ...
... опыт», учится на своих и чужих ошибках и постепенно выучиваться принимать правильные решения – если не оптимальные, то почти оптимальные. Попробуем проиллюстрировать процесс имитационного моделирования через сравнение с классической математической моделью. Этапы процесса построения математической модели сложной системы: 1. Формулируются основные вопросы о поведении ...





0 комментариев