Навигация
2.3 Пример 3
Рассмотрим пример: найдём приближенно объём, ограниченный поверхностями
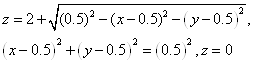
Искомый объём численно равен величине интеграла
![]() (3.7)
(3.7)
Так как в области V ![]() , вводим новую переменную
, вводим новую переменную ![]() , в результате чего интеграл (3.7) переходит в интеграл
, в результате чего интеграл (3.7) переходит в интеграл
![]() (3.8)
(3.8)
где ![]() область, ограниченная поверхностями
область, ограниченная поверхностями

т.е. ![]() принадлежит единичному кубу
принадлежит единичному кубу ![]() .
.
Берём теперь три равномерно распределенные на отрезке ![]() последовательности случайных чисел и записываем их в качестве координат
последовательности случайных чисел и записываем их в качестве координат ![]() случайных точек в табл. 3.2. Затем проверяем, какие из этих точек принадлежат области
случайных точек в табл. 3.2. Затем проверяем, какие из этих точек принадлежат области ![]() .
.
Таблица 3.2
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 | 0.577 | 0.116 | 0.077 | 0.384 | 0.147 | 1 | 0.667 | 1 | 1 | ||
| 2 | 0.716 | 0.930 | 0.216 | 0.430 | 0.232 | 0.993 | 0.193 | 0.231 | 0 | ||
| 3 | 0.737 | 0.930 | 0.237 | 0.430 | 0.241 | 1 | 0.242 | 1 | 1 | ||
| 4 | 0.701 | 0.428 | 0.201 | 0.072 | 0.045 | 0.940 | 0.140 | 0.122 | 1 | ||
| 5 | 0.170 | 0.529 | 0.330 | 0.029 | 0.110 | 1 | 0.610 | 1 | 1 | ||
| 6 | 0.533 | 0.095 | 0.033 | 0.405 | 0.165 | 1 | 0.131 | 1 | 1 | ||
| 7 | 0.432 | 0.996 | 0.068 | 0.496 | 0.251 | 0 | 0.352 | 1 | 0 | ||
| 8 | 0.263 | 0.699 | 0.237 | 0.199 | 0.096 | 1 | 0.645 | 1 | 1 | ||
| 9 | 0.059 | 0.313 | 0.441 | 0.187 | 0.229 | 1 | 0.646 | 1 | 1 | ||
| 10 | 0.663 | 0.270 | 0.163 | 0.230 | 0.080 | 1 | 0.680 | 1 | 1 | ||
| 11 | 0.355 | 0.653 | 0.145 | 0.153 | 0.046 | 1 | 0.577 | 1 | 1 | ||
| 12 | 0.094 | 0.934 | 0.406 | 0.434 | 0.353 | 0 | 0.716 | 1 | 0 | ||
| 13 | 0.303 | 0.058 | 0.197 | 0.442 | 0.234 | 1 | 0.737 | 1 | 1 | ||
| 14 | 0.552 | 0.003 | 0.052 | 0.497 | 0.250 | 1 | 0.701 | 1 | 1 | ||
| 15 | 0.640 | 0.882 | 0.140 | 0.382 | 0.165 | 1 | 0.169 | 1 | 1 | ||
| 16 | 0.205 | 0.986 | 0.295 | 0.486 | 0.323 | 0 | 0.533 | 1 | 0 | ||
| 17 | 0.002 | 0.521 | 0.498 | 0.021 | 0.248 | 1 | 0.432 | 1 | 1 | ||
| 18 | 0.557 | 0.918 | 0.057 | 0.418 | 0.178 | 1 | 0.263 | 1 | 1 | ||
| 19 | 0.870 | 0.071 | 0.370 | 0.429 | 0.318 | 0 | 0.059 | 1 | 0 | ||
| 20 | 0.313 | 0.139 | 0.187 | 0.361 | 0.185 | 1 | 0.663 | 1 | 1 | ||
|
| |||||||||||
Заполним табл. 3.2 по правилу:
1) выделяем точки, у которых ![]() , и полагаем для них
, и полагаем для них ![]()
2) среди выделенных точек области ![]() принадлежат те, для которых выполняется неравенство
принадлежат те, для которых выполняется неравенство ![]() .
.
Для этих точек ![]() , для остальных
, для остальных ![]()
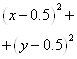
3) вычисляем ![]() . Области
. Области ![]() принадлежат те точки, для которых
принадлежат те точки, для которых ![]()
4) среди точек, у которых ![]() , области
, области ![]() принадлежат те точки, координаты которых удовлетворяют неравенству
принадлежат те точки, координаты которых удовлетворяют неравенству
![]()
Для этих точек ![]() .
.
В примере общее количество точек ![]() , а число точек, принадлежащих области
, а число точек, принадлежащих области ![]() , равно 15. По формуле (3.6) получаем
, равно 15. По формуле (3.6) получаем
![]() , а точное значение объёма
, а точное значение объёма ![]() равно
равно ![]()
Погрешность формулы (3.6) обратно пропорциональна корню из числа испытаний, т.е. ![]() .
.
Это означает, что для обеспечения большой точности число точек ![]() должно быть очень велико. Но так как приближенные формулы (3.3), (3.6) не зависят от размерности интеграла, метод Монте-Карло оказывается выгодным при вычислении интегралов большой размерности.
должно быть очень велико. Но так как приближенные формулы (3.3), (3.6) не зависят от размерности интеграла, метод Монте-Карло оказывается выгодным при вычислении интегралов большой размерности.
Заключение
Процесс выполнения данной работы представлял большой интерес и послужил хорошей возможностью для приобретения новых знаний и навыков, а также закрепления уже полученных.
Были рассмотрены основные свойства метода Монте-Карло и создана программа, показывающая возможности данного метода при использовании ЭВМ.
Было выяснено, что методом Монте-Карло можно решать разнообразные задачи, в том числе вычисление интегралов, не прибегая к сложным математическим вычислениям. Простота алгоритма метода Монте-Карло позволяет успешно реализовывать их на ЭВМ.
Список литературы
1. Бусленко Н.П. Метод статистического моделирования – М.: Статистика, 1970. – 112 с.
2. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 1966. – 664 с.
3. Епанешников А.М., Епанешников В.А. Программирование в среде TURBO PASCAL 7.0 – М.: Диалог-МИФИ, 1998. – 288 с.
4. Ермаков С.М. Метод Монте-Карло и смежные вопросы – М.: Наука, 1975–472 с.
5. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 367 с.
6. Соболь И.М. Метод Монте-Карло – М.: Наука, 1985. – 80 c.
Приложения
1. Таблица 400 случайных цифр
| 86615 | 90795 | 66155 | 66434 | 56558 | 12332 | 94377 | 57802 |
| 69186 | 03393 | 42505 | 99224 | 88955 | 53758 | 91641 | 18867 |
| 41686 | 42163 | 85181 | 38967 | 33181 | 72664 | 53807 | 00607 |
| 86522 | 47171 | 88059 | 89342 | 67248 | 09082 | 12311 | 90316 |
| 72587 | 93000 | 89688 | 78416 | 27589 | 99528 | 14480 | 50961 |
| 52452 | 42499 | 33346 | 83935 | 79130 | 90410 | 45420 | 77757 |
| 76773 | 97526 | 27256 | 66447 | 25731 | 37525 | 16287 | 66181 |
| 04825 | 82134 | 80317 | 75120 | 45904 | 75601 | 70492 | 10274 |
| 87113 | 84778 | 45863 | 24520 | 19976 | 04925 | 07824 | 76044 |
| 84754 | 57616 | 38132 | 64294 | 15218 | 49286 | 89571 | 42903 |
2. Таблица 40 случайных чисел, равномерно распределенных на отрезке ![]()
| 0.57705 | 0.35483 | 0.11578 | 0.65339 |
| 0.71618 | 0.09393 | 0.93045 | 0.93382 |
| 0.73710 | 0.30304 | 0.93011 | 0.05758 |
| 0.70131 | 0.55186 | 0.42844 | 0.00336 |
| 0.16961 | 0.64003 | 0.52906 | 0.88222 |
| 0.53324 | 0.20514 | 0.09461 | 0.98585 |
| 0.43166 | 0.00188 | 0.99602 | 0.52103 |
| 0.26275 | 0.55709 | 0.69962 | 0.91827 |
| 0.05926 | 0.86977 | 0.31311 | 0.07069 |
| 0.66289 | 0.31303 | 0.27004 | 0.13928 |
3. Листинг программы
Вычисляются значения кратных интегралов из примера 2–3.
program pmk;
uses crt;
var
w, u, h, k, v, y, p, s, g, x, x2, y2, z2, niu, Integral, Integral2:real;
n, m, i, a, b, e1, e2, e, e3, e4, e5:integer;
begin
clrscr;
writeln ('vychisleniye dvoynogo integrala iz primera 1');
writeln ('vvedite kolichestvo sluchaynykh tochek:');
readln(n);
for i:=1 to n do
begin
g:=random;
p:=random;
x:=g;
y:=p;
if ((0.5<=x) and (x<=1)) then e1:=1
else e1:=0;
if ((0<=y) and (y<=2*x-1)) then e2:=1
else e2:=0;
e:=e1*e2;
if e=1 then s:=s+x*x+y*y;
if e=1 then a:=a+1;
v:=1/4;
delay(1000);
end;
Integral:=(v/a)*(s);
writeln ('summa=', s:5:5);
writeln ('dvoynoy integral iz 1 primera =', Integral:5:5);
writeln ('vychisleniye troynogo integrala iz primera 2');
writeln ('vvedite kolichestvo sluchaynykh tochek:');
readln(m);
for i:=1 to m do
begin
w:=random;
u:=random;
h:=random;
x2:=w;
y2:=u;
niu:=h;
if niu<=0.8 then e3:=1;
if (x2–0.5)*(x2–0.5)+(y2–0.5)*(y2–0.5)<=(0.5)*(0.5) then e4:=1
else e4:=0;
e5:=e3*e4;
if (((0.8<niu) and (niu<1)) and ((x2–0.5)*(x2–0.5)+(y2–0.5)*(y2–0.5)+6.25*(niu-0.8)*(niu-0.8)<=(0.5)*(0.5))) then e5:=1;
if e5=1 then b:=b+1;
delay(1000);
end;
Integral2:=2.5*(b/m);
writeln ('kvo pod t =', b:5);
writeln ('troynoy integral iz 2 primera =', Integral2:5:5);
readln;
end.
4. Пример работы программы при 10000 случайных точек
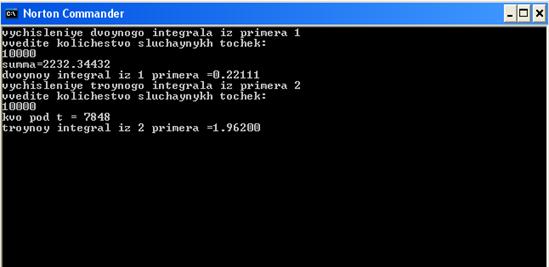
Похожие работы
... частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*. §2. Оценка погрешности метода Монте-Карло. Пусть для получения оценки a* математического ожидания а случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х) ...
... в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для исследования различного рода сложных систем (автоматического управления, экономических, биологических и т.д.). Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой а: (1) ...
етка – одно из простейших средств получения случайных чисел с хорошим равномерным распределением, на использовании которых основан этот метод. Метод Монте – Карло это статистический метод. Его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, в теориях передачи информации, при исследовании сложных ...
... опыт», учится на своих и чужих ошибках и постепенно выучиваться принимать правильные решения – если не оптимальные, то почти оптимальные. Попробуем проиллюстрировать процесс имитационного моделирования через сравнение с классической математической моделью. Этапы процесса построения математической модели сложной системы: 1. Формулируются основные вопросы о поведении ...
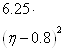





0 комментариев