Навигация
Интегрирование по частям
6. Интегрирование по частям
Теорема 4. Пусть функции ![]() и
и ![]() имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке ![]() . Тогда имеет место следующая формула интегрирования по частям:
. Тогда имеет место следующая формула интегрирования по частям:
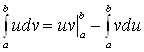 . (4)
. (4)
Доказательство
Так как ![]() , то функция
, то функция ![]() является первообразной для функции
является первообразной для функции ![]() . Тогда по формуле Ньютона–Лейбница получаем
. Тогда по формуле Ньютона–Лейбница получаем
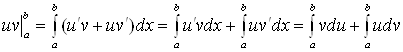 ,
,
откуда
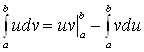 .
.
Пример 6. Вычислить 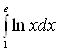 .
.
Решение. Положим ![]() , отсюда
, отсюда ![]() . По формуле (4) находим
. По формуле (4) находим
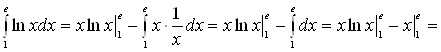
![]() .
.
Пример 7. Вычислить 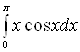 .
.
Решение. Пусть ![]() , тогда
, тогда ![]() . Применяя формулу интегрирования по частям, получаем
. Применяя формулу интегрирования по частям, получаем

![]() .
.
Пример 8. Вычислить 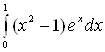 .
.
Решение. Полагая ![]() , определяем
, определяем ![]() . Следовательно:
. Следовательно:
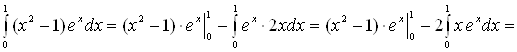
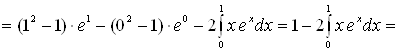 [к полученному интегра-лу снова применяем формулу интегрирования по частям:
[к полученному интегра-лу снова применяем формулу интегрирования по частям: ![]() ; следовательно:
; следовательно: ![]() ] =
] = ![]() =
= ![]()
![]() .
.
Лекция 2. Применение определенных интегралов. Несобственные интегралы
1. Площадь криволинейной трапеции
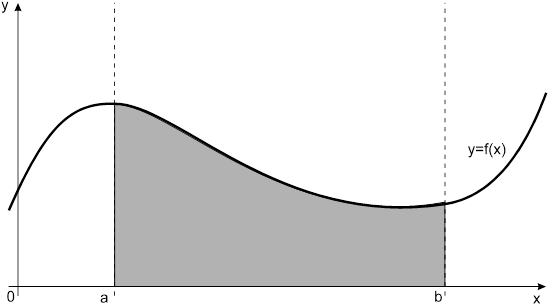
Пусть функция ![]() неотрицательна и непрерывна на отрезке
неотрицательна и непрерывна на отрезке ![]() . Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью
. Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью ![]() , слева и справа – прямыми
, слева и справа – прямыми ![]() и
и ![]() (см. рис. 2) вычисляется по формуле
(см. рис. 2) вычисляется по формуле
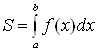 . (5)
. (5)
Пример 9. Найти площадь фигуры, ограниченной линией ![]() и осью
и осью ![]() .
.
Решение. Графиком функции ![]() является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью
является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью ![]() (прямой
(прямой ![]() ). Для этого решаем систему уравнений
). Для этого решаем систему уравнений
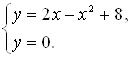
Получаем: ![]() , откуда
, откуда ![]() ,
, ![]() ; следовательно,
; следовательно, ![]() ,
, ![]() .
.
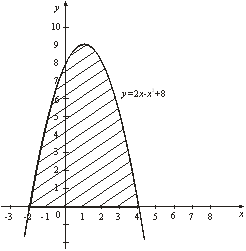
Рис. 3
Площадь фигуры находим по формуле (5):
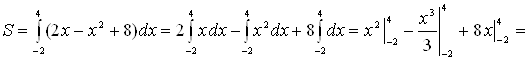
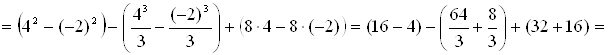
![]() (кв. ед.).
(кв. ед.).
Если функция ![]() неположительна и непрерывна на отрезке
неположительна и непрерывна на отрезке ![]() , то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью
, то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью ![]() , слева и справа – прямыми
, слева и справа – прямыми ![]() и
и ![]() , вычисляется по формуле
, вычисляется по формуле
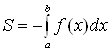 . (6)
. (6)
В случае если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 4) равна алгебраической сумме соответствующих определенных интегралов:
и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 4) равна алгебраической сумме соответствующих определенных интегралов:
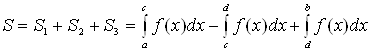 . (7)
. (7)
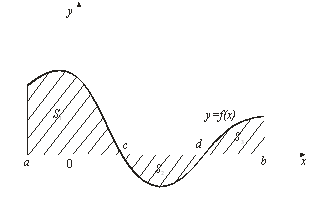
Рис. 4
Пример 10. Вычислить площадь фигуры, ограниченной осью ![]() и графиком функции
и графиком функции ![]() при
при ![]() .
.
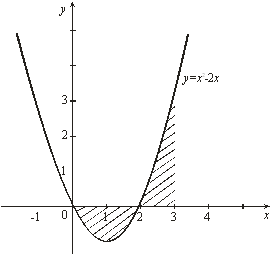
Рис. 5
Решение. Сделаем чертеж (рис. 5). Искомая площадь представляет собой сумму площадей ![]() и
и ![]() . Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему
. Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему 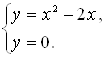 Получим
Получим ![]() ,
, ![]() . Следовательно:
. Следовательно:
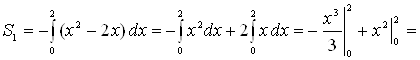
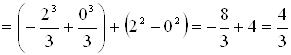 ;
;
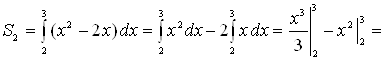
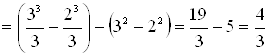 .
.
Таким образом, площадь ![]() заштрихованной фигуры равна
заштрихованной фигуры равна
![]() (кв. ед.).
(кв. ед.).
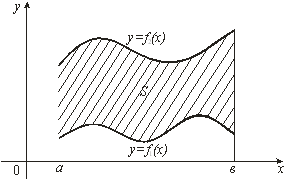
Рис. 6
Пусть, наконец, криволинейная трапеция ограничена сверху и снизу графиками непрерывных на отрезке ![]() функций
функций ![]() и
и ![]() ,
,
а слева и справа – прямыми ![]() и
и ![]() (рис. 6). Тогда ее площадь вычисляется по формуле
(рис. 6). Тогда ее площадь вычисляется по формуле
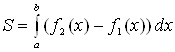 . (8)
. (8)
Пример 11. Найти площадь фигуры, ограниченной линиями ![]() и
и ![]() .
.
Решение. Данная фигура изображена на рис. 7. Площадь ее вычислим по формуле (8). Решая систему уравнений  находим
находим ![]() ,
, ![]() ; следовательно,
; следовательно, ![]() ,
, ![]() . На отрезке
. На отрезке ![]() имеем:
имеем: ![]() . Значит, в формуле (8) в качестве
. Значит, в формуле (8) в качестве ![]() возьмем x, а в качестве
возьмем x, а в качестве ![]() –
– ![]() . Получим:
. Получим:
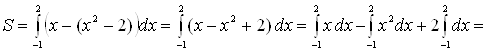
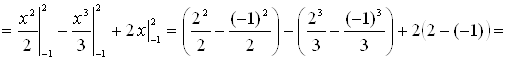
![]() (кв. ед.).
(кв. ед.).
Более сложные задачи на вычисление площадей решают путем разбиения фигуры на непересекающиеся части и вычисления площади всей фигуры как суммы площадей этих частей.
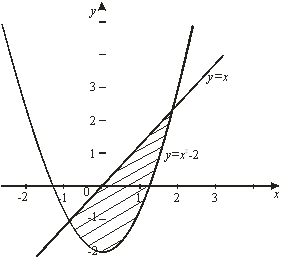
Рис. 7
Пример 12. Найти площадь фигуры, ограниченной линиями ![]() ,
, ![]()
![]() ,
, ![]() .
.
Решение. Сделаем чертеж (рис. 8). Данную фигуру можно рассматривать как криволинейную трапецию, ограниченную снизу осью ![]() , слева и справа – прямыми
, слева и справа – прямыми ![]() и
и ![]() , сверху – графиками функций
, сверху – графиками функций ![]() и
и ![]() . Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой
. Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой ![]() на две части (1 – это абсцисса точки пересечения линий
на две части (1 – это абсцисса точки пересечения линий ![]() и
и ![]() ). Площадь каждой из этих частей находим по формуле (4):
). Площадь каждой из этих частей находим по формуле (4):
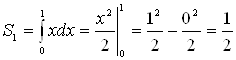 (кв. ед.);
(кв. ед.); 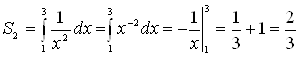 (кв. ед.). Следовательно:
(кв. ед.). Следовательно:
![]() (кв. ед.).
(кв. ед.).
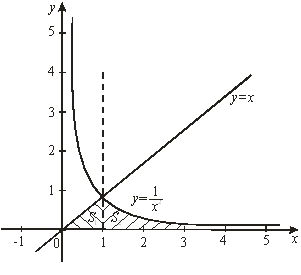
Рис. 8
|
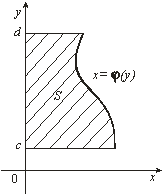
Рис. 9
В заключение отметим, что если криволинейная трапеция ограничена прямыми ![]() и
и ![]() , осью
, осью ![]() и непрерывной на
и непрерывной на ![]() кривой
кривой ![]() (рис. 9), то ее площадь находится по формуле
(рис. 9), то ее площадь находится по формуле
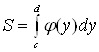 .
.
Похожие работы
... с содержится в промежутке . Таким образом, мы вновь получили лангранжеву форму дополнительного члена. 5. Заключение. В курсовой работе даны определения определенного и несобственного интеграла и его виды, рассмотрены вопросы некоторого приложения определенного интеграла. В частности, формула Валлиса, имеющая историческое значение, как первое представление числа p в виде предела легко вычисляемой ...
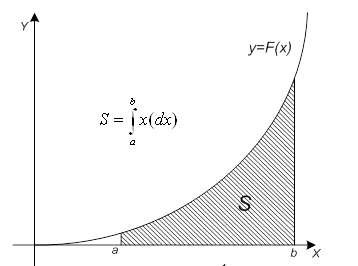
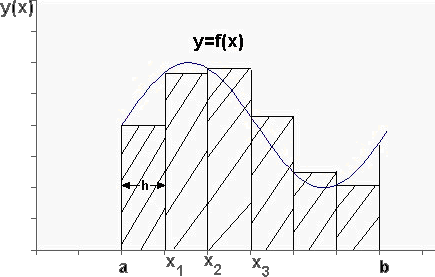
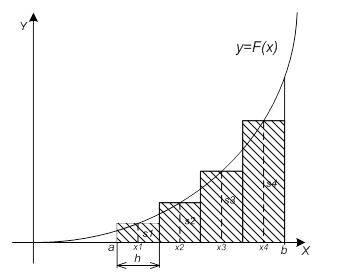
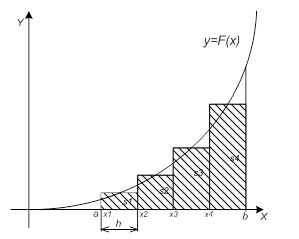
ределенный интеграл функции типа численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= (Рис. 1). Есть два метода вычисления этой площади или определенного интеграла — метод трапеций (Рис. 2) и метод средних прямоугольников (Рис. 3). Рис. 1. Криволинейная трапеция. Рис. 2. Метод трапеций. Рис. 3. Метод средних прямоугольников. По методам ...
... n (увеличения числа интеграций) повышается точность приближенного вычисления интегралов Задание на лабораторную работу 1) Написать программы вычисления определенного интеграла методами: средних, правых прямоугольников, трапеции и методом Симпсона. Выполнить интегрирование следующих функций: 1. f(x)=x f(x)=x2 f(x)= x3 f(x)= x4 на отрезке [0, 1] с шагом , , 2. f(x)= f(x)= f(x)= ...
... ( процедура TABL ) и интеграл. 4. Заключение и выводы. Таким образом очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное. Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же ...


0 комментариев