Навигация
Замена переменной в определенном интеграле
15080
знаков
0
таблиц
15
изображений
5. Замена переменной в определенном интеграле
Теорема 3. Пусть функция 
непрерывна на отрезке 
. Тогда, если: 1) функция 
и ее производная 
непрерывны при 
; 2) множеством значений функции 
при является отрезок ; 3) 
, 
, то справедлива формула
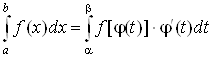, (3)
которая называется формулой замены переменной в определенном интеграле.
Заметим, что как и в случае неопределенного интеграла, использование замены переменной позволяет упростить исходный интеграл, приблизив его к табличному. При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования – достаточно лишь найти новые пределы интегрирования 
и 
(для этого надо решить относительно переменной t уравнения 
и 
)).
На практике часто вместо подстановки используют подстановку 
. В этом случае нахождение новых пределов интегрирования по переменной t упрощается: 
, 
.
Пример 3. Вычислить интеграл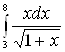 
Решение. Введем новую переменную по формуле 
. Определим 
и 
. Возведя в квадрат обе части равенства , получим 
, откуда 
. Находим новые пределы интегрирования. Для этого в формулу подставим старые пределы 
и 
. Получим: 
, откуда 
и, следовательно, 
; 
, откуда 
и, следовательно, 
. Таким образом:
.
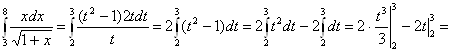
Пример 4. Вычислить интеграл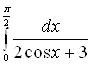 
.
Решение. Воспользуемся универсальной тригонометрической подстановкой. Положим 
, откуда 
, 
. Найдем новые пределы интегрирования: если 
, то 
; если 
, то 
. Значит, 
. Следовательно:
.
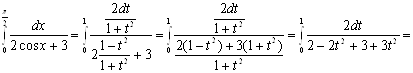
Пример 5. Вычислить интеграл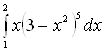 
.
Решение. Положим 
, тогда 
, откуда 
. Находим новые пределы интегрирования: 
; 
. Имеем: 
. Следовательно:
.
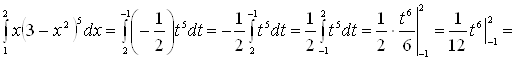
Похожие работы
... с содержится в промежутке . Таким образом, мы вновь получили лангранжеву форму дополнительного члена. 5. Заключение. В курсовой работе даны определения определенного и несобственного интеграла и его виды, рассмотрены вопросы некоторого приложения определенного интеграла. В частности, формула Валлиса, имеющая историческое значение, как первое представление числа p в виде предела легко вычисляемой ...
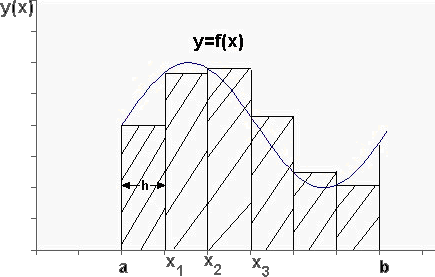
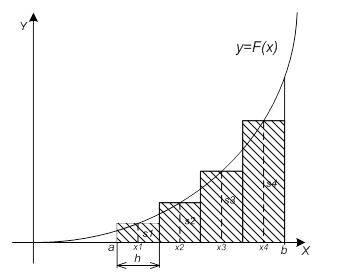
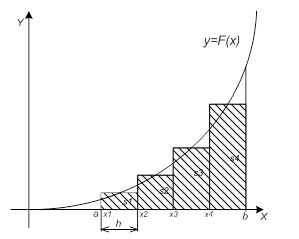
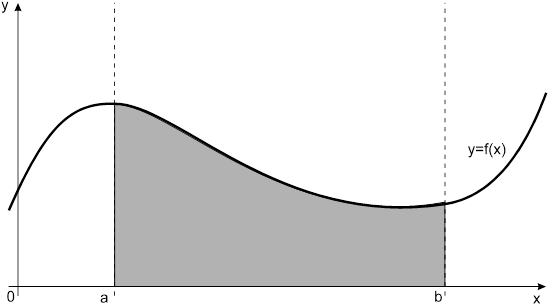
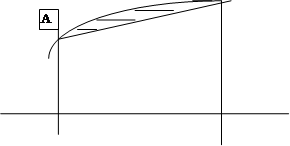
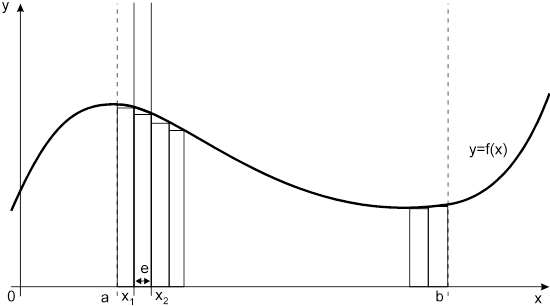
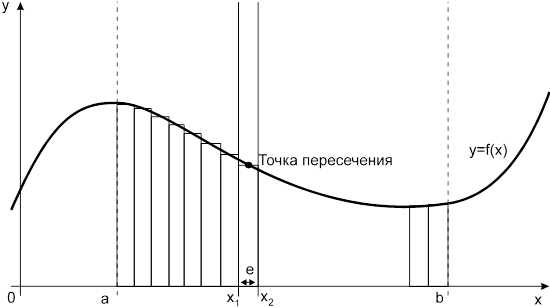
ределенный интеграл функции типа численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= (Рис. 1). Есть два метода вычисления этой площади или определенного интеграла — метод трапеций (Рис. 2) и метод средних прямоугольников (Рис. 3). Рис. 1. Криволинейная трапеция. Рис. 2. Метод трапеций. Рис. 3. Метод средних прямоугольников. По методам ...
... n (увеличения числа интеграций) повышается точность приближенного вычисления интегралов Задание на лабораторную работу 1) Написать программы вычисления определенного интеграла методами: средних, правых прямоугольников, трапеции и методом Симпсона. Выполнить интегрирование следующих функций: 1. f(x)=x f(x)=x2 f(x)= x3 f(x)= x4 на отрезке [0, 1] с шагом , , 2. f(x)= f(x)= f(x)= ...
... ( процедура TABL ) и интеграл. 4. Заключение и выводы. Таким образом очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное. Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же ...
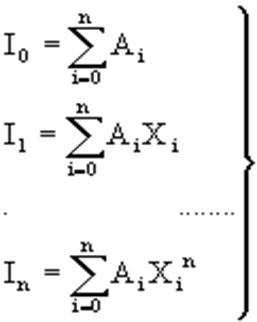
0 комментариев