Навигация
2. Объем тела вращения
Пусть криволинейная трапеция, ограниченная графиком непрерывной на отрезке 
функции 
, осью 
, прямыми 
и 
, вращается вокруг оси (рис. 10). Тогда объем полученного тела вращения вычисляется по формуле
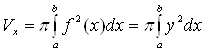. (9)
Пример 13. Вычислить объем тела, полученного вращением вокруг оси криволинейной трапеции, ограниченной гиперболой 
, прямыми 
, 
и осью .
Решение. Сделаем чертеж (рис. 11).
Из условия задачи следует, что 
, 
. По формуле (9) получаем
.
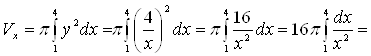
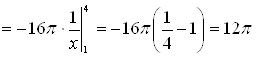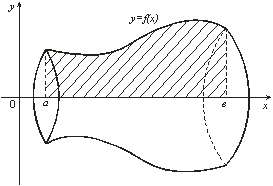
Рис. 10
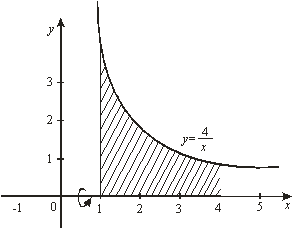
Рис. 11
Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной прямыми у = с и у = d, осью Оу и графиком непрерывной на отрезке 
функции 
(рис. 12), определяется по формуле
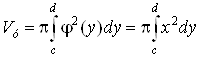. (10)
|
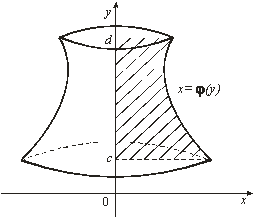
Рис. 12
Пример 14. Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями х2 = 4у, у = 4, х = 0 (рис. 13).
Решение. В соответствии с условием задачи находим пределы интегрирования: 
, 
. По формуле (10) получаем:
.
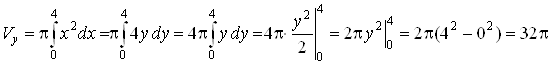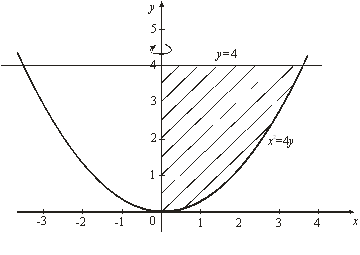
Рис. 13
3. Длина дуги плоской кривой
Пусть кривая 
, заданная уравнением , где 
, лежит в плоскости 
(рис. 14).
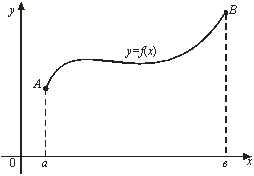
Рис. 14
Определение. Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.
Если функция и ее производная 
непрерывны на отрезке , то длина дуги кривой вычисляется по формуле
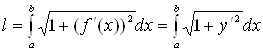. (11)
Пример 15. Вычислить длину дуги кривой 
, заключенной между точками, для которых 
.
Решение. Из условия задачи имеем 
. По формуле (11) получаем:
.
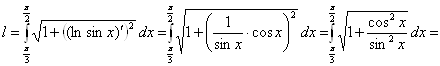
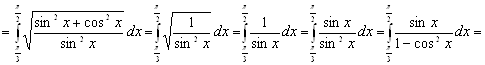
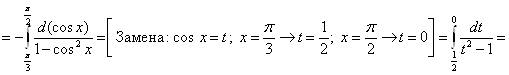
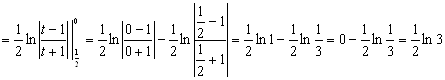Похожие работы
... с содержится в промежутке . Таким образом, мы вновь получили лангранжеву форму дополнительного члена. 5. Заключение. В курсовой работе даны определения определенного и несобственного интеграла и его виды, рассмотрены вопросы некоторого приложения определенного интеграла. В частности, формула Валлиса, имеющая историческое значение, как первое представление числа p в виде предела легко вычисляемой ...
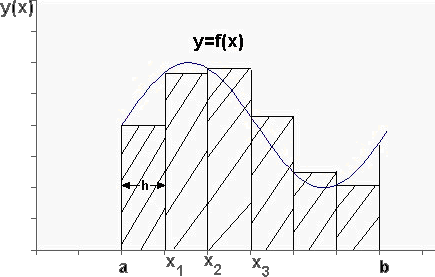
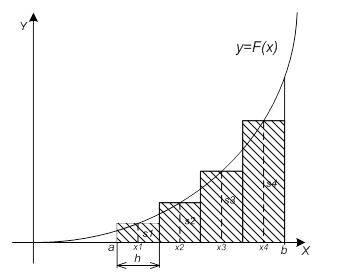
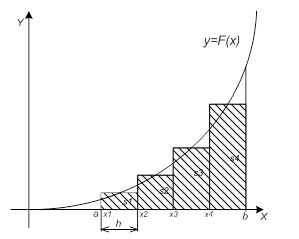
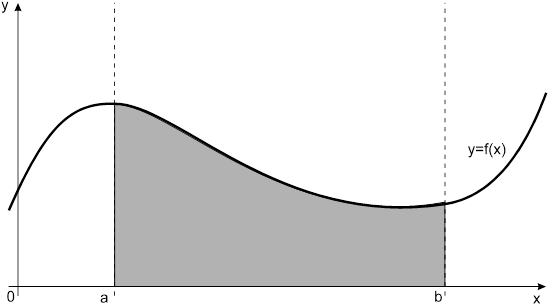
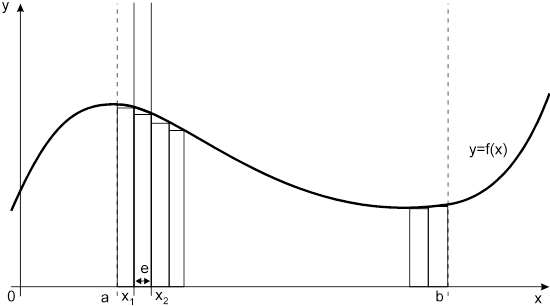
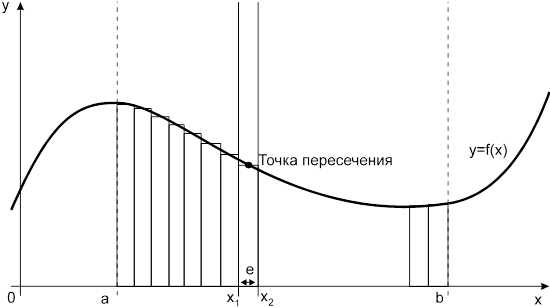
ределенный интеграл функции типа численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= (Рис. 1). Есть два метода вычисления этой площади или определенного интеграла — метод трапеций (Рис. 2) и метод средних прямоугольников (Рис. 3). Рис. 1. Криволинейная трапеция. Рис. 2. Метод трапеций. Рис. 3. Метод средних прямоугольников. По методам ...
... n (увеличения числа интеграций) повышается точность приближенного вычисления интегралов Задание на лабораторную работу 1) Написать программы вычисления определенного интеграла методами: средних, правых прямоугольников, трапеции и методом Симпсона. Выполнить интегрирование следующих функций: 1. f(x)=x f(x)=x2 f(x)= x3 f(x)= x4 на отрезке [0, 1] с шагом , , 2. f(x)= f(x)= f(x)= ...
... ( процедура TABL ) и интеграл. 4. Заключение и выводы. Таким образом очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное. Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же ...
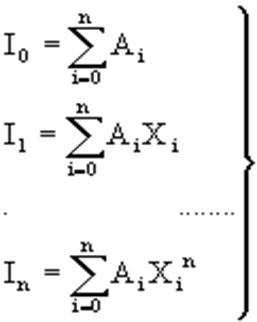
0 комментариев