Навигация
6. Дивергенція
Означення. Дивергенцією векторного поля ![]() називається скалярна функція
називається скалярна функція
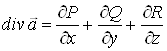 .
.
Слово «дивергенція» означає «розбіжність».
Дивергенція характеризує густину джерел даного векторного поля в розглянутій точці.
Розглянемо, наприклад, електричне поле точкового заряду ![]() , розміщеного в початку координат:
, розміщеного в початку координат:
![]() ,
,
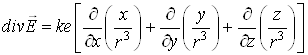 .
.
Оскільки 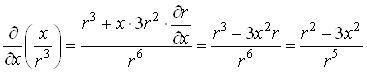 , і аналогічно
, і аналогічно 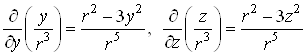 , то
, то 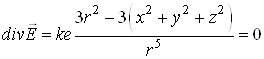
(при ![]() ). Цей результат означає відсутність поля у довільній точці, крім початку координат. В початку координат
). Цей результат означає відсутність поля у довільній точці, крім початку координат. В початку координат ![]() .
.
7. Ротор
Означення. Ротором (або вихором) векторного поля
![]()
називається вектор-функція
 .
.
Зокрема, для плоского поля ![]() маємо
маємо
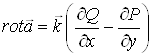 .
.
Розглянемо тверде тіло, яке обертається навколо осі ![]() із сталою кутовою швидкістю
із сталою кутовою швидкістю ![]() (рис. 1).
(рис. 1).
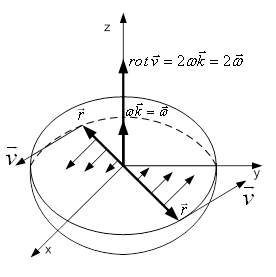
Рисунок 1 – Тверде тіло, яке обертається навколо осі ![]()
Векторне поле швидкостей ![]() точок цього тіла можна подати у вигляді
точок цього тіла можна подати у вигляді
 .
.
Знайдемо ротор поля швидкостей ![]() :
:
 .
.
Таким чином, ![]() є сталим вектором, напрямленим уздовж осі обертання
є сталим вектором, напрямленим уздовж осі обертання ![]() , а його модуль дорівнює подвоєній кутовій швидкості обертання тіла:
, а його модуль дорівнює подвоєній кутовій швидкості обертання тіла:
![]() .
.
Розглянемо потенціальне поле ![]() . Його потенціал
. Його потенціал 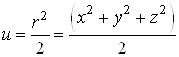 . Обчислимо ротор цього поля:
. Обчислимо ротор цього поля:
 .
.
Взагалі, ротор довільного потенціального поля дорівнює нулю (див. підрозділ 2). Тому кажуть, що потенціальне поле є безвихровим.
8. Соленоїдальне поле
Векторне поле ![]() називається соленоїдальним в області
називається соленоїдальним в області ![]() , якщо в цій області
, якщо в цій області ![]() . Оскільки
. Оскільки ![]() характеризує густину джерел поля
характеризує густину джерел поля ![]() , то в тій області, де поле соленоїдальне, немає джерел цього поля.
, то в тій області, де поле соленоїдальне, немає джерел цього поля.
Наприклад, електричне поле ![]() точкового заряду соленоїдальне (задовольняє умову
точкового заряду соленоїдальне (задовольняє умову ![]() ) всюди поза точкою, де знаходиться заряд (в цій точці
) всюди поза точкою, де знаходиться заряд (в цій точці ![]() ). Векторні лінії соленоїдального поля не можуть починатися або закінчуватися на межі області, або бути замкненими кривими. Прикладом соленоїдального поля з замкненими векторними лініями є магнітне поле, яке створюється струмом у провіднику.
). Векторні лінії соленоїдального поля не можуть починатися або закінчуватися на межі області, або бути замкненими кривими. Прикладом соленоїдального поля з замкненими векторними лініями є магнітне поле, яке створюється струмом у провіднику.
Якщо векторне поле ![]() можна подати як ротор деякого векторного поля
можна подати як ротор деякого векторного поля ![]() , тобто
, тобто ![]() , то вектор – функція
, то вектор – функція ![]() називається векторним потенціалом поля
називається векторним потенціалом поля ![]() .
.
Можна перевірити (див. докладніше п. 2), що ![]() , тобто поле
, тобто поле ![]() є соленоїдальним.
є соленоїдальним.
Довільне векторне поле можна подати у вигляді суми потенціального і соленоїдального полів.
Похожие работы
... кта та алгоритму його функціонування, або алгоритму процесу, а також уявлення опису на різноманітних мовах здійснюється взаємодією людини і ЕОМ. Система автоматизованого проектування - це комплеск засобів автоматизації проектування, взаємозв’язаних з необхідними підрозділами проектної організації або колективом спеціалістів (користувачем системи), які виконують автоматизоване проектування. САПР ...
... на малому , g(x,y) стала y1 = y(x0 ) + y(x0 ) + g(x0, y0 ) x Повторюючи знайдемо y2 = y(x1+x) y(x1) + g(x1, y1 ) x yn= yn-1+ g(xn-1 ,yn-1) x, (n=0,1,2…) нахил дотичної визначається початковою точкою інтервалу. 2.3. Програма для комп’ютера. Алгоритм методу. 1. Вибирається початкова умова, величина кроку і кількість ітерацій (кроків). 2. Визначається y і нахил у початковій точці ...
... мальне значення показникунадійності, при якому приймається рішення про орєінтованийзвязок назвем порогом показника надійності і позначимо (). Для можливості порівняння результатів у різних парах змінних в одній задачі системного синтезу корисно ввести відносний показник надійності. Відносним показником надійності ηij приняття рішення про напрям звязку між змінними xj → xi (стрілка в ...
... здійснювати на ведучому навчальному матеріалі. 6. Формування прийомів розумової діяльності вимагає врахування індивідуально-вікових особливостей учнів. 1.2 Формування уміння порівнювати в процесі навчання математики Порівняння в навчанні – це розумова операція, за допомогою якої встановлюються риси подібності і відмінності між визначеними предметами і явищами. Пізнання будь-якого ...






0 комментариев