Навигация
9. Оператор Гамільтона
Згадаємо, що символ ![]() називається оператором частинної похідної по
називається оператором частинної похідної по ![]() . Під добутком цього оператора на функцію
. Під добутком цього оператора на функцію ![]() розумітимемо частинну похідну
розумітимемо частинну похідну ![]() , тобто
, тобто ![]() . Аналогічно,
. Аналогічно, ![]() і
і ![]() – оператори частинних похідних по
– оператори частинних похідних по ![]() і по
і по ![]() .
.
Введемо векторний оператор «набла» або оператор Гамільтона:
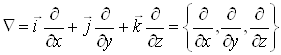 .
.
За допомогою цього символічного (операторного) «вектора» зручно записувати і виконувати операції векторного аналізу.
У результаті множення вектора ![]() на скалярну функцію
на скалярну функцію ![]() отримуємо
отримуємо ![]() :
:
 .
.
Скалярний добуток вектора ![]() на вектор – функцію
на вектор – функцію ![]() дає
дає ![]() :
:
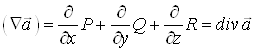 .
.
Векторний добуток вектора ![]() на вектор – функцію
на вектор – функцію ![]() дає
дає ![]() :
:
 .
.
10. Нестаціонарні поля
Нехай в області ![]() визначено нестаціонарне скалярне поле
визначено нестаціонарне скалярне поле ![]() : величина
: величина ![]() є функцією точки
є функцією точки ![]() і часу
і часу ![]() . Приклад такого поля – змінний з часом розподіл температури в будь-якому середовищі (наприклад, в потоці рідини). Розглянемо точку
. Приклад такого поля – змінний з часом розподіл температури в будь-якому середовищі (наприклад, в потоці рідини). Розглянемо точку ![]() , яка рухається в області
, яка рухається в області ![]() (частинку рідини). Координати точки (частинки) змінюються з часом за відомим законом
(частинку рідини). Координати точки (частинки) змінюються з часом за відомим законом ![]() . Величина
. Величина ![]() в рухомій точці
в рухомій точці ![]() є складеною функцією
є складеною функцією ![]() :
:
![]() .
.
Обчислимо похідну по ![]() цієї функції (вона називається повною похідною). За правилом диференціювання складеної функції знаходимо
цієї функції (вона називається повною похідною). За правилом диференціювання складеної функції знаходимо
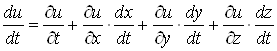 .
.
Вводячи в точці ![]() вектор швидкості
вектор швидкості 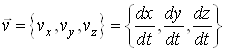 , отримуємо
, отримуємо
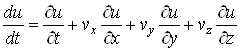
Або
![]() .(11)
.(11)
Аналогічно, якщо в області ![]() задано нестаціонарне векторне поле
задано нестаціонарне векторне поле ![]() , то для рухомої точки
, то для рухомої точки ![]() векторна величина
векторна величина ![]() є складеною функцією
є складеною функцією ![]() :
: ![]() . Повну похідну по
. Повну похідну по ![]() для кожної координати вектор – функції
для кожної координати вектор – функції ![]() можна обчислити за формулою (11). Помноживши результати на базисні вектори
можна обчислити за формулою (11). Помноживши результати на базисні вектори ![]() і складаючи, отримуємо
і складаючи, отримуємо
![]() .(12)
.(12)
У формулах (11) і (12) доданки ![]() і
і ![]() виражають швидкості зміни величин
виражають швидкості зміни величин ![]() та
та ![]() з часом при фіксованих координатах, тобто характеризують локальні зміни цих величин, і тому називаються локальними похідними. Доданки
з часом при фіксованих координатах, тобто характеризують локальні зміни цих величин, і тому називаються локальними похідними. Доданки ![]() і
і ![]() утворюються за рахунок зміни координат точки, її руху (конвекції). Тому ці доданки у виразах повних похідних називаються конвективними похідними.
утворюються за рахунок зміни координат точки, її руху (конвекції). Тому ці доданки у виразах повних похідних називаються конвективними похідними.
Локальні похідні характеризують нестаціонарність розглянутого поля у даній точці простору. Конвективні похідні характеризують неоднорідність поля у даний момент часу.
Похожие работы
... кта та алгоритму його функціонування, або алгоритму процесу, а також уявлення опису на різноманітних мовах здійснюється взаємодією людини і ЕОМ. Система автоматизованого проектування - це комплеск засобів автоматизації проектування, взаємозв’язаних з необхідними підрозділами проектної організації або колективом спеціалістів (користувачем системи), які виконують автоматизоване проектування. САПР ...
... на малому , g(x,y) стала y1 = y(x0 ) + y(x0 ) + g(x0, y0 ) x Повторюючи знайдемо y2 = y(x1+x) y(x1) + g(x1, y1 ) x yn= yn-1+ g(xn-1 ,yn-1) x, (n=0,1,2…) нахил дотичної визначається початковою точкою інтервалу. 2.3. Програма для комп’ютера. Алгоритм методу. 1. Вибирається початкова умова, величина кроку і кількість ітерацій (кроків). 2. Визначається y і нахил у початковій точці ...
... мальне значення показникунадійності, при якому приймається рішення про орєінтованийзвязок назвем порогом показника надійності і позначимо (). Для можливості порівняння результатів у різних парах змінних в одній задачі системного синтезу корисно ввести відносний показник надійності. Відносним показником надійності ηij приняття рішення про напрям звязку між змінними xj → xi (стрілка в ...
... здійснювати на ведучому навчальному матеріалі. 6. Формування прийомів розумової діяльності вимагає врахування індивідуально-вікових особливостей учнів. 1.2 Формування уміння порівнювати в процесі навчання математики Порівняння в навчанні – це розумова операція, за допомогою якої встановлюються риси подібності і відмінності між визначеними предметами і явищами. Пізнання будь-якого ...






0 комментариев