Задание координатных систем 20-графиков и их пересчет

13.1.3. Задание координатных систем 20-графиков и их пересчет

В версии Maple V R4 параметр coords задает 15 типов координатных систем для двумерных графиков. По умолчанию задана прямоугольная (Декартовая) система координат (coords=cartesian). При использовании других координатных систем координаты точек для них (u,v) преобразуются в координаты (х,у) как (u, v) -> (x, у). Ниже приведены наименования систем координат (значении параметра coords) и соответствующие формулы преобразования:

bipolar

х = sinh(v)/(cosh(v)-cos(u)) у = sin(u)/(cosh(v)-cos(u))

cardiod

х = [/2*(u'2-v~2}/(u'2+v'2Y2 у = u*v/(ir2+v"2)-2

cartesian

х = u у = v

cassinian

x = a*2«(l/2)/2*((exp(2*u)+2*exp(l^)*cos(v)+l)«(l/2) +

exp(u)*cos(v)+l)"(l/2) у = a*2»(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)"(l/2) -

exp(u)*ws(v)-l)'-(\/2)}

elliptic

x = cosh(u)*cos(v) у = sinh(u)*sin(v)

hyperbolic

x = ((iT2+v-2)-(l/2)+u)-(l/2) у = ((^2+у'2Г(\/2)-иУ(1/2)

invcassinian

x = a*2~(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)"(l/2) +

exp(u)*cos(v)+l)»(l/2)/(exp(2*u)+2*exp(u)*cos(v)+l)-(l/2) у = a*2»(l/2)/2*((exp(2*u)-^2*exp(u)*cos(v)+l)-(l/2) -

exp(u)*cos(v)-l)»(l/2)/(exp(2*u)+2*exp(u)*cos(v)+l)-(l/2)

invelliptic

x = a*cosh(u)*cos(v)/(cosh(u)"2-sin(v)'2) у = a*sinh(u)*sin(v)/(cosh(u)"2-sin(v)»2)

logarithmic

x = ii/Pi*ln(u'2+v'2) у = 2*a/Pi*arctan(v/u)

logcosh

x = a/Pi*\n(c.osh(uy2-sm(vy2} у = 2*a/Pi*arctan(tanh(u)*tan(v))

maxwell

x = a/Pi*(u+l+exp(u)*cos(v)) у = a/Pi*(v+exp(u)*sin(v))

parabolic

x = (u'2-v^2)/2 у = u*v

I'I-

polar

x = u*cos(v) у = u*sin(v)

rose

x = ((u'2+v'2Y(\/2)+ur(\/2)/(u~2+v'2)-(i/2) у = ((^2+v'2)-(\/2)-u)-(\/2)/(u'2+^2r(\/2)

tangent

x= u/tu^+v^) у = v/(iT2+v'2)

13.1.4. Управление стилем и цветом линий 20-графиков

Maple V R4 позволяет воспроизводить на одном графике множество кривых. При этом возникает необходимость из выделения. Для этого можно использовать построение линии разными стилями и разными цветами и разной толщиной линий. Набор средств выделения кривых позволяет уверенно различать их как на экране цветного дисплея и распечатках цветным струйным принтером, так и при печати монохромными принтерами.

Параметр style позволяет задавать следующие стили для линий графиков:

SPISV = POINT или point — график выводится по точкам;

LINE или line — график выводится линией.

Если задано построение графика точками то параметр symbol позволяет представить точки в виде различных символов, например, прямоугольника, креста, окружности или ромба.

Другой параметр color позволяет установить обширный набор цветов линий графиков:

aquamarine black blue navy coral cyan brown gold green gray grey khaki magenta maroon orange pink plum red sienna tan turquoise violet wheat white yellow

Различные цветовые оттенки получаются использованием RGB-комбинаций базовых цветов: red — красный, green — зеленый, blue — синий. Приведем перевод ряда других комбинированных цветов: black — черный, white — белый, khaki — цвет «хаки», gold — золотистый, orange — оранжевый, violet — фиолетовый, yellow — желтый и т.д. Перевод цветов некоторых оттенков на русский язык не всегда однозначен и потому не приводится. Средства управления стилем графиков дают возможность легко выделять различные кривые на одном рисунке, даже если для выделения не используются цвета.

13.2. Примеры построения основных типов 20-графиков

13.2.1. Построение графиков одной функции

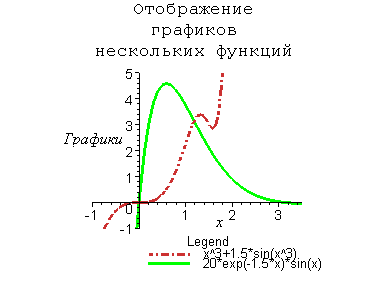
При построении графика одной функции она записывается в явном виде на место шаблона f. Примеры построения графика одной функции представлены на рис. 13.1. Обратите внимание на то, что график функции sin(x)/x строится без

характерного провала в точке х=0, который наблюдается при построении графиков этой функции многими программами. Он связан с используемым в них правилом — функция задается равной нулю, если ее числитель равен нулю. Данная функция в этой точке дает устранимую неопределенность 0/0->1, что и учитывает графический процессор системы Maple V.

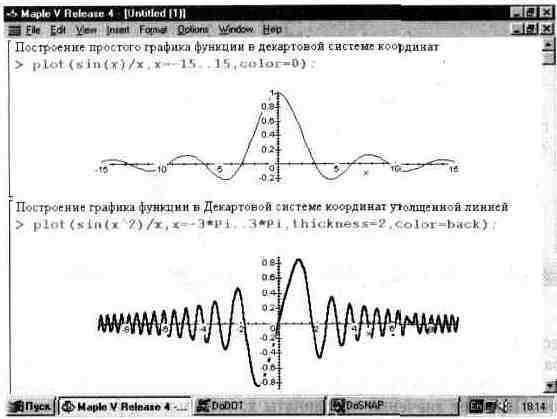
Рис. 13.1. Примеры построения графиков одной функции.

При построении графиков одной функции могут быть введены указатели масштабов и различные опции, например задания цвета кривой, толщины линии, которой строится график функции и другие параметры. К примеру, запись в списке параметров со1ог=0 (не документированная возможность) или запись color=black задают вывод кривых черным цветом, а запись thinkness=2 задает во втором примере рис. 13.1 построение графика линией, удвоенной в сравнении с обычной толщиной.

13.2.2. Управление масштабом графиков

Для управления масштабом графиков служат указатели масштабов. В ряде случаев их можно не применять и система автоматически задает приемлемые масштабы. Однако их явное применение позволяет задать масштаб «вручную». Иногда соответствующее задание масштаба случайно или целенаправленно ведет к отсечению части графика — например на рис. 13.2 в первом примере отсечена верхняя часть графика.

Правильный выбор масштаба повышает представительность графиков функций. Рекомендуется вначале пробовать строить такие графики с автоматическим масштабированием, а уже затем использовать указатели масштабов.

Похожие работы

Двумерная графика системы Maple

Скачать

18394

1

6

... для работы с графикой. Также на этом же рисунке отображено контекстное меню, появляющееся при щелчке правой кнопкой мыши, когда указатель расположен в области графического вывода. При выделении двумерной графики на рабочем листе меню Insert, Spreadsheet и Options, находящиеся в строке основного меню, заменяются новыми Style, Legend. Axes, Projection, Animation и Export, которые позволяют изменить ...

Основы работы с системой MathCAD 7. 0 PRO

Скачать

78056

0

20

... Windows будем подразумевать операционные системы Windows 95 и Windows NT, имеющие практически идентичный интерфейс пользователя. С точки зрения работы в них системы MathCAD 7. 0 разницы между этими операционными системами нет. 1. 2. Инсталляция и запуск системы Системы MathCAD 7. 0 PRO поставляются на CD-ROM (возможна поставка минимальных версий и на 3, 5-дюймовых дискетах). При этом полная ...

Системы стабилизации и ориентации

Скачать

26620

1

17

... размечают в логарифмическом масштабе, где изменение частоты в 10 раз называется декадой, амплитуду  откладывают в децибелах и фазу q в градусах. 1.4 Анализ устойчивости непрерывных и дискретных систем Системы стабилизации должны обеспечивать устойчивость и заданную точность регулирования отклонений углов и координат центра масс ЛА от программных значений. При этом могут налагаться ограничения ...

Вычислительная математика

Скачать

100779

18

23

... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...