Задание координатных систем 20-графиков и их пересчет
Графики функций в неограниченном масштабе
Построение графиков функций, заданных их именами
Построение ЗО-графиков с помощью функция plot3d
Примеры построения трехмерных поверхностей с помощью функции plot3d
Задание 30-графики в виде процедуры
Графика пакета plots 13.6.1. Общая характеристика пакета plots
Построение графиков функций в двумерной полярной системе координат
Графики в разных системах координат
Построение анимационных 20-графиков
Графическое представление решений дифференциальных уравнений
Функция DEplot3d из пакета DEtools
Графическая функция phaseportrait
Графическая визуализация решений и анимация
Визуализация Ньютоновых итераций
Анимация разложения импульса в ряд Фурье
Работа с электронными таблицами
Трансформация графиков в реальном масштабе времени
Расширяемое меню справочной системы
Навигация
Примеры построения трехмерных поверхностей с помощью функции plot3d
Графика в системе Maple V
109435
знаков
6
таблиц
96
изображений
13.4. Примеры построения трехмерных поверхностей с помощью функции plot3d
13.4.1. Простейшее построение ЗО-поверхности с разным стилем
На рис. 13.15 показано два примера простейших построений графиков трехмерной поверхности. По умолчанию строится каркасная поверхность с функциональной окраской тонких линий каркаса и удалением невидимых линий. Чтобы график выглядел более четким, построение в первом примере задано линиями черного цвета с помощью параметра color-black.
Рис. 13.15. Примеры простейшего построения трехмерных поверхностей.
Во втором примере та же поверхность построена с параметром style=patch, что приводит к появлению ее функциональной окраски (увы, на рисунках в книге воспринимаемой как окраска оттенками серого цвета). Функциональная окраска делает рисунки более информативными.
Помимо значения path, можно задавать ряд других стилей для построения трехмерных поверхностей: point — точками, contour — контурными линиями, line — линиями, hidden — линиями каркаса с удалением невидимых линий, wireframe — линиями каркаса со всеми видимыми линиями, patchnogrid — с раскраской, но без линий каркаса, patchcontour — раскраска с линиями равного уровня.
Цвет трехмерного графика может задаваться (как и у двумерного) опцией со1ог=с, где с — цвет (оттенки цвета указывались выше). Возможно еще два алгоритма задания цвета:
HUE — алгоритм с заданием цвета в виде color=f(x,y);
RGB — алгоритм с заданием цвета в виде color=[exprr,exprg,exprb], где выражения exprr, exprg и exprb — выражения, задающие относительную значимость (от О до 1) основных цветов (красного — red, зеленого — green и синего — blue).
Удачный выбор углов обзора фигуры и применение функциональной окраски позволяют придать построениям трехмерных фигур весьма эффектный и реалистический вид.
13.4.2. Построение фигур в различных системах координат
Как отмечалось, вид графика трехмерной поверхности существенно зависит от выбора координатной системы. Рис. 13.16 показывает пример построения нелинейного конуса в цилиндрической системе координат. Для задания такой системы координат используется параметр coords=cylindrical.
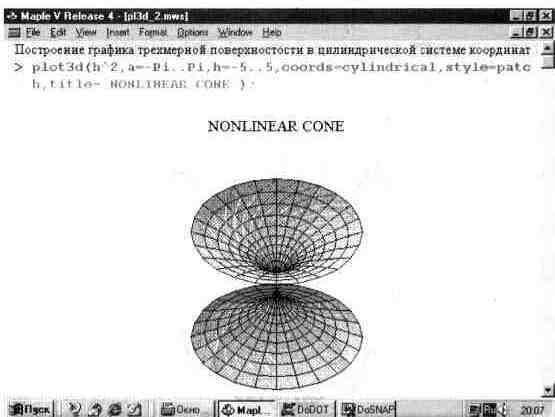
Рис. 13.16. Нелинейная цилиндрическая поверхность.
При построении этой фигуры также использована цветная функциональная окраска. Кроме того, этот пример иллюстрирует вывод над рисунком титульной надписи.
Приведем еще один пример построения трехмерной поверхности — на этот раз в сферической системе координат (рис. 13.17). Здесь функция задана вообще элементарно просто — в виде числа 1. Но поскольку выбрана сферическая система координат, то строится поверхность шара единичного радиуса.
При этом построении также задана функциональная окраска поверхности и вывод титульной надписи.
О том, насколько необычным может быть график той или иной функции в различных системах координат свидетельствует рис. 13.18. На нем показан график параметрически заданной функции от одной координаты t — sin(t"3), построенный в сферической системе координат.
Кстати, рис. 13.18 иллюстрирует возможность одновременного наблюдения более чем одного окна — в данном случае двух окон. В одном окне задано построение графика, а в другом — построен сам график. При построении графика в отдельном
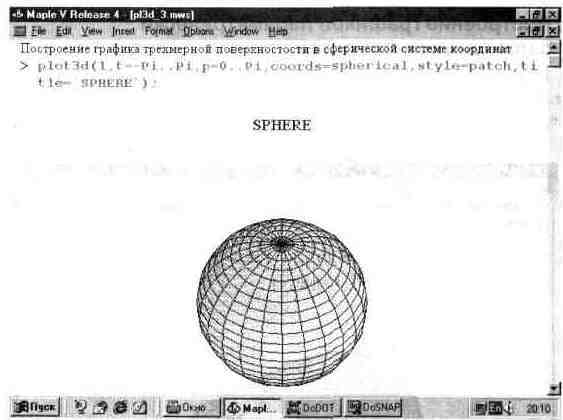
Рис. 13.17. Построение шарообразной поверхности в сферической системе координат.
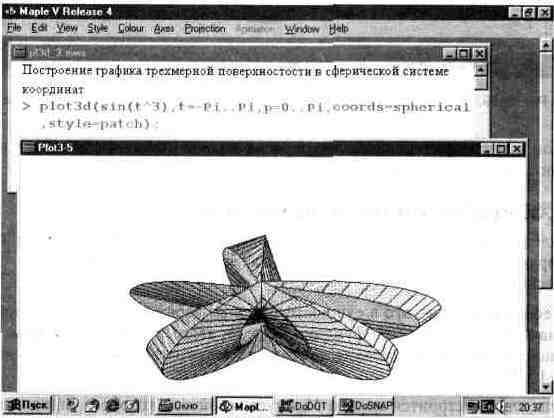
Рис. 13.18. График еще одной поверхности в сферической системе координат.
окне появляется панель форматирования графика. С помощью ее довольно наглядных кнопок-пиктограмм можно легко скорректировать вспомогательные параметры графика (окраску, наличие линий каркаса, ориентацию и др.).
13.4.3. Построение графиков параметрически заданных поверхностей
На рис. 13.19 показано построение поверхности при полном ее параметрическом задании. В этом случае поверхность задается тремя формулами, содержащимися в списке.
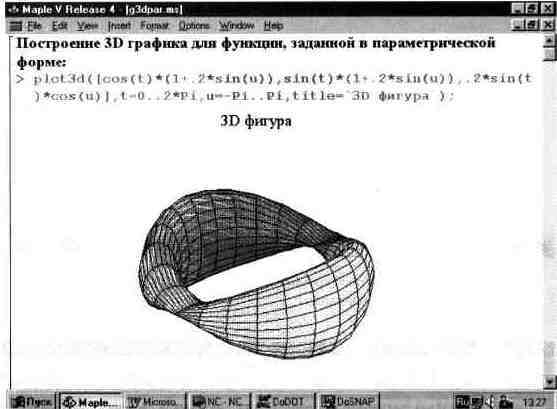
Рис. 3.19. График ЗО-поверхности при полном параметрическом ее задании.
В данном случае функциональная окраска задана из меню, поэтому в состав функции соответствующий параметр не введен.
13.4.4. ЗО-график как графический объект
Принадлежность функции plot и plot3D к функциям (в ряде книг их именуют операторами, командами или процедурами) наглядно выявляется при создании графических объектов.
Графический объект — это в сущности обычная переменная, которой присваивается значение графической функции. После этого такая переменная, будучи вызванной, вызывает построение соответствующего графика. Пример этого дан на рис. 13.20.
В данном случае строится кольцо Мебиуса, свойства которого (например, плавный переход с одной стороны ленты на другую) уже много веков будоражат воображение людей.
Похожие работы
... для работы с графикой. Также на этом же рисунке отображено контекстное меню, появляющееся при щелчке правой кнопкой мыши, когда указатель расположен в области графического вывода. При выделении двумерной графики на рабочем листе меню Insert, Spreadsheet и Options, находящиеся в строке основного меню, заменяются новыми Style, Legend. Axes, Projection, Animation и Export, которые позволяют изменить ...
... Windows будем подразумевать операционные системы Windows 95 и Windows NT, имеющие практически идентичный интерфейс пользователя. С точки зрения работы в них системы MathCAD 7. 0 разницы между этими операционными системами нет. 1. 2. Инсталляция и запуск системы Системы MathCAD 7. 0 PRO поставляются на CD-ROM (возможна поставка минимальных версий и на 3, 5-дюймовых дискетах). При этом полная ...
... размечают в логарифмическом масштабе, где изменение частоты в 10 раз называется декадой, амплитуду откладывают в децибелах и фазу q в градусах. 1.4 Анализ устойчивости непрерывных и дискретных систем Системы стабилизации должны обеспечивать устойчивость и заданную точность регулирования отклонений углов и координат центра масс ЛА от программных значений. При этом могут налагаться ограничения ...
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...
0 комментариев