Навигация
Трансформация графиков в реальном масштабе времени
14.5. Трансформация графиков в реальном масштабе времени
В Maple V R5 введена новая и безусловно важная возможность — трансформация ЗО-графиков в реальном масштабе времени. В прежних версиях выделенный
график заменялся параллелограммом, который можно было вращать мышью. Однако сам график на время трансформации просто исчезал и для его перестройки надо было запускать пиктограмму с буквой R (Redraw). Процесс перестройки графика даже на достаточно производительных ПК (класса Pentium 200) шел несколько секунд.
Похоже, разработчикам новой реализации системы удалось существенно ускорить алгоритмы перестройки ЗО-графиков, что позволило реализовать вращение фигур в пространстве в реальном масштабе времени. Рис. 14.11 показывает, как это происходит.
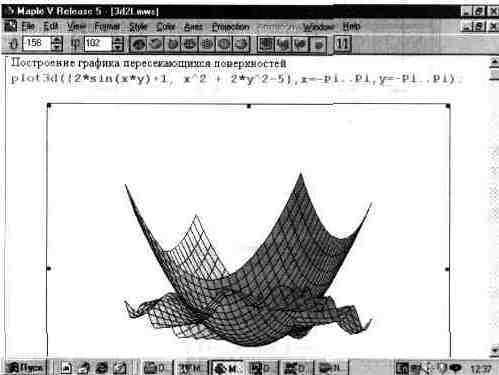
Рис. 14.11. Трансформация SD-графика в реальном масштабе времени.
Хотя некоторая инерционность процесса перестройки заметна даже при работе на ПК с процессором Pentium 200 ММХ и с ОЗУ 32 Мбайта, ощущение от реального поворота фигуры остается вполне отчетливым. Эта возможность позволяет быстро найти оптимальный угол зрения на фигуру, при которой ее особенности, например пики и впадины, выявляются в наиболее полной мере. Заметно существенное улучшение и алгоритма построения линий пересечения сложных фигур в пространстве. Наглядная и эффектная функциональная окраска фигур выполняется теперь по умолчанию.
К сожалению, при использовании созданных ранее в реализации R4 сложных графических объектов (в виде нескольких компонентов) этот алгоритм иногда дает сбои. Пример такого случая показан на рис. 14.12. В данном случае тор вращается сам по себе, в результате обмотки оказываются не на нем, а где-то в стороне.
Возможно, что это вызвано именно тем, что исходный документ готовился в предшествующей реализации системы. Кстати, при попытке загрузки файла от предшествующей реализации системы выводится окно с предупреждающей надписью и предлагает преобразовать файл в формат, присущий новой реализации. Это окно показано на рис. 14.13.
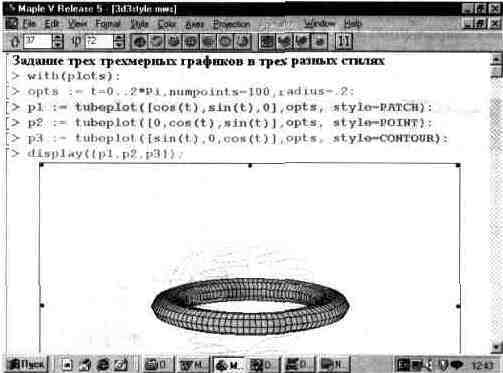
Рис. 14.12. Сбои трансформации сложного ЗО-объекта.
Ответьте «Да», если вы намерены преобразовать файл, и «Нет» при отказе от этой операции. В целом можно считать, что Maple V R5 вполне обеспечивает совместимость файлов документов с предшествующей версией системы.
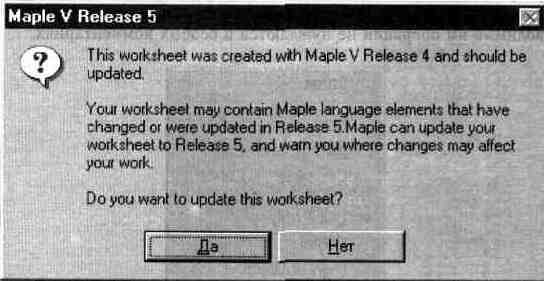
Рис. 14.13. Окно, сообщающее о загрузке файла предшествующей реализации и необходимости его преобразования.
14.6. Контекстно-зависимое меню операций
Сторонников легкой работы с системой (надеемся, что и вы, читатель, относитесь к таковым) порадует еще одна, хотя и не принципиальная, но очень полезная возможность — контекстно-зависимое меню операций (в том числе математических). Она реализуется нажатием правой клавиши мыши при указании маркером мыши заданного объекта.
На рис. 14.14 показан экран системы и контекстно-зависимое меню, относящееся к введенному выражению sin(x)/x, находящемуся в строке вывода. При этом меню дает перечень операций, которые можно делать с этим выражением — например, дифференцировать, интегрировать, строить график и т.д.
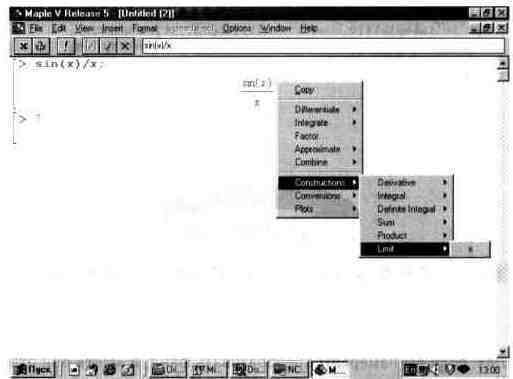
Рис. 14.14. Контекстно-зависимое меню для математических выражении.
Если маркер мыши стоит в строке ввода, то появляется меню, представляющее основные операции по работе с текстами. Окно этого меню показано на рис. 14.15. Вводимые им операции не нуждаются в особых комментариях.

Рис. 14.15. Меню для работы с текстами
Применение контекстно-зависимых меню облегчает работу с системой и делает ее похожей на работу в среде современных программных средств под Windows 95. В целом оно реализует принцип «ввел выражение — нажал кнопку — получил результат».
14.7. Быстрое построение графиков
Быстрое построение 2D- и ЗО-графиков — еще одна приятная «мелочь» новой реализации Maple V R4, облегчающая визуализацию вычислений. Ее тоже можно реализовать с помощью контекстно-зависимого меню. Достаточно вызвать его для выбранного выражения, как с помощью операции Plot можно построить график. При этом система Maple V R5 сама определяет (по виду выражения), какой же график надо строить.
Рис. 14.16 показывает быстрое построение графика функции sin(x) /x указанным способом. При этом вам даже не надо помнить, какой функцией обеспечивается построение графика. В дальнейшем оформление графика можно изменить операциями форматирования.
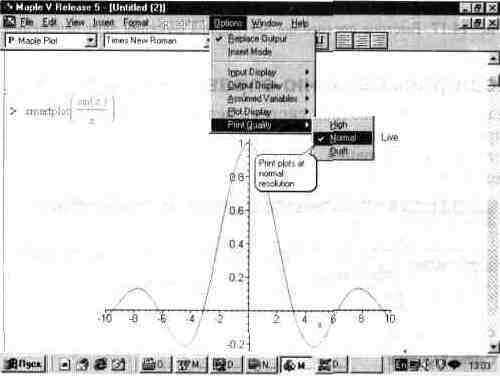
Рис. 14.16. Быстрое построение 20-графика функции одной переменной.
Кстати говоря, в позиции главного меню Options появилась новая операция Print Quality — качество печати (рис. 14.16). Она позволяет выбрать три степени качества печати: High (высшее). Normal (нормальное) и Draft (черновое).
Столь же просто обстоит дело с построением иных графиков. Так, на рис. 14.17 представлено построение ЗО-графика функции двух переменных — sin(x*y/5). При этом можно воспользоваться описанным ранее приемом — трансформацией графика в реальном масштабе времени для получения наивысшей выразительности графика.
Maple V R5 имеет ряд дополнительных функций для такого рода построений. Две из них видны на рис. 14.16 и 14.17. Это функции smartplot и smartplot3d. С другими можно ознакомиться с помощью справочной системы.
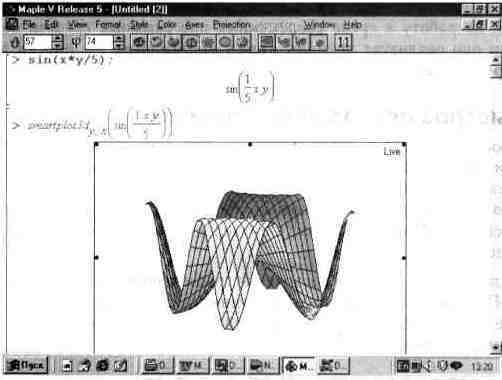
Рис. 14.17. Быстрое построение SD-графика функции двух переменных.
Похожие работы
... для работы с графикой. Также на этом же рисунке отображено контекстное меню, появляющееся при щелчке правой кнопкой мыши, когда указатель расположен в области графического вывода. При выделении двумерной графики на рабочем листе меню Insert, Spreadsheet и Options, находящиеся в строке основного меню, заменяются новыми Style, Legend. Axes, Projection, Animation и Export, которые позволяют изменить ...
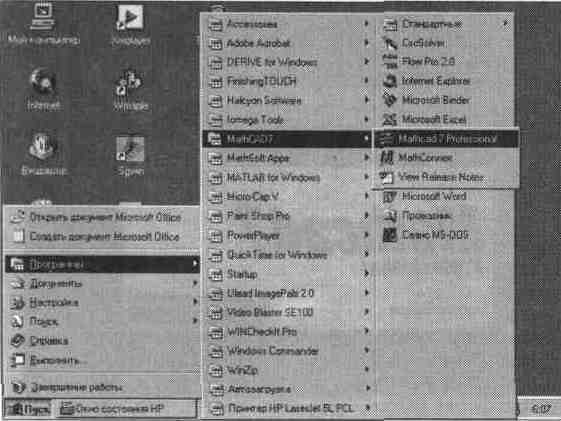
... Windows будем подразумевать операционные системы Windows 95 и Windows NT, имеющие практически идентичный интерфейс пользователя. С точки зрения работы в них системы MathCAD 7. 0 разницы между этими операционными системами нет. 1. 2. Инсталляция и запуск системы Системы MathCAD 7. 0 PRO поставляются на CD-ROM (возможна поставка минимальных версий и на 3, 5-дюймовых дискетах). При этом полная ...
... размечают в логарифмическом масштабе, где изменение частоты в 10 раз называется декадой, амплитуду откладывают в децибелах и фазу q в градусах. 1.4 Анализ устойчивости непрерывных и дискретных систем Системы стабилизации должны обеспечивать устойчивость и заданную точность регулирования отклонений углов и координат центра масс ЛА от программных значений. При этом могут налагаться ограничения ...
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...



0 комментариев