Задание координатных систем 20-графиков и их пересчет
Графики функций в неограниченном масштабе
Построение графиков функций, заданных их именами
Построение ЗО-графиков с помощью функция plot3d
Примеры построения трехмерных поверхностей с помощью функции plot3d
Задание 30-графики в виде процедуры
Графика пакета plots 13.6.1. Общая характеристика пакета plots
Построение графиков функций в двумерной полярной системе координат
Графики в разных системах координат
Построение анимационных 20-графиков
Графическое представление решений дифференциальных уравнений
Функция DEplot3d из пакета DEtools
Графическая функция phaseportrait
Графическая визуализация решений и анимация
Визуализация Ньютоновых итераций
Анимация разложения импульса в ряд Фурье
Работа с электронными таблицами
Трансформация графиков в реальном масштабе времени
Расширяемое меню справочной системы
Навигация
Графическая визуализация решений и анимация
Графика в системе Maple V
109435
знаков
6
таблиц
96
изображений
13.11. Графическая визуализация решений и анимация
Выше уже не раз графика использовалась для визуализации решений математических задач. Так, многие особенности даже функций одной переменной вида f(x) могут быть выявлены с помощью графика функций. Затем можно точно вычислить корни функции (точки перехода через 0), экстремумы, крутизну наклона (произ-
водную) в заданных точках и т.д. Еще более информативна в этом отношении трехмерная графика — для большинства функций двух переменных вида z(x,y) нужно очень богатое математическое воображение, чтобы представить их вид — особенно в одной из многих десятков координатных систем.
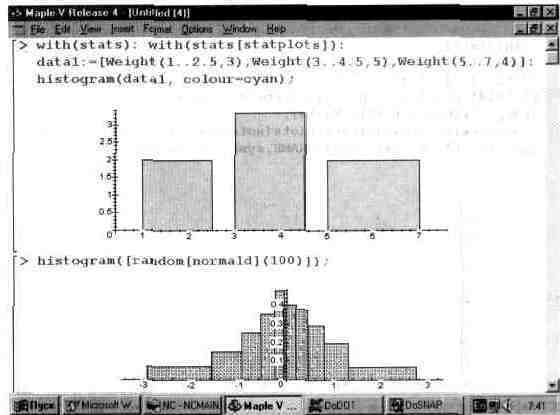
Рис. 13.63. Построение гистограмм.
Однако некоторые виды графиков трудно представить себе даже при наличии такого воображения. В этом отношении Maple V предоставляет поистине уникальные возможности в обеспечении простой и быстрой визуализации решений. Ниже мы рассмотрим несколько наиболее характерных примеров такой визуализации. В них нет наиболее показательных примеров визуализации решений дифференциальных уравнений, поскольку они уже были рассмотрены.
13.11.1. Иллюстрация решения систем линейных уравнений
Системы линейных уравнений могут решаться как с помощью функции solve, так и с помощью матричных методов. Замечательной возможностью функции solve является возможность решения относительно ограниченного числа переменных. Например, систему линейных уравнений с переменными х, у, z, t и v можно решить относительно только первых трех переменных х, у и z. При этом решения будут функциями относительно переменных t и v и можно построить наглядный график решения (рис. 13.64).
На рис. 13.64 система задана пятью равенствами: е1, е2, еЗ, е4 и е5. Затем функцией solve получено вначале решение для всех переменных (для иллюстрации), а затем для трех переменных х, у и z. Для получения решения в виде списка, а не множества, как в первом случае для всех переменных, использована функция подстановки subs. После этого функция plot3d строит плоскость решения в пространстве.
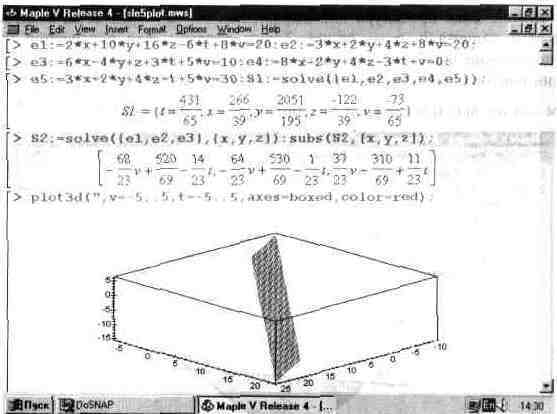
Рис. 13.64. График, представляющий решения системы линейных уравнений.
13.11.2. Графическая визуализация решения системы неравенств
Пожалуй, еще более полезным и наглядным является визуализация решения системы уравнений в виде неравенств. В пакете расширения plots имеется специальная графическая функция inequal, которая строит все граничные линии неравенств и позволяет раскрасить разделенные ими области различными цветами:
inequal(ineqs, xspec, yspec, options).
Параметры этой функции: ineqs — одно или более неравенство или равенство или список неравенств или равенств, xspec — xvar == min_x..max_x, yspec — yvar = min_y..max_y и о — необязательные опции, например указывающие на цвета линий, представляющих неравенства или равенства, и областей, образованных этими линиями и границами графика. Пример применения этой функции представлен на рис. 13.65.
Обратите внимание на задание опций цветов: optionsfasfeasibly задает цвет внутренней области, для которой удовлетворяются все неравенства (равенства), optionsopen и optionsclose задают цвета открытых и закрытых областей графика, optionsexcluded для цвета внешних областей. График дает весьма наглядную интерпретацию действия ряда неравенств (или равенств).
13.11.3. Конформные отображения на комплексной плоскости
Объем данной книги не позволяет объяснить столь тонкое понятие, как конформные отображения на комплексной плоскости. Ограничимся лишь указанием на то, что в пакете plots имеется функция для таких отображений:
conformal(F,rl ,г2,о);
где F — комплексная процедура или выражение, rl, r2 — области, задаваемые в виде а..Ь или name=a..b, о — опции. Таким образом, для построения нужного графика достаточно задать нужное выражение и области изменения rl и г2. Пример построения конформных изображений для трех выражении дан на рис. 13.66.
В данном случае все три графика построены в отдельных окнах.
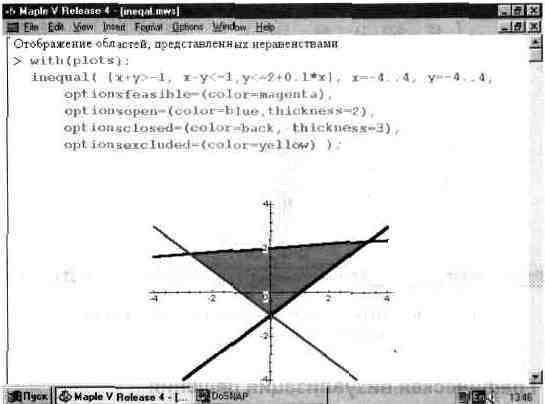
Рис. 13.65. Пример графической интерпретации решения системы неравенств.
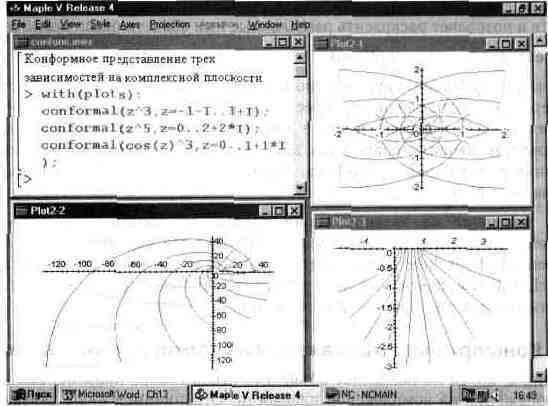
Рис. 13.66. Конформное отображение на комплексной плоскости графиков трех зависимостей.
13.11.4. Графическое представление содержимого матрицы
Многие вычисления имеют результаты, представляемые в форме матриц. Иногда такие результаты можно наглядно представить графически, например, в виде столбиковой диаграммы. Она представляет собой множество столбиков квадратного сечения, расположенных на плоскости, образованной осями строк (row) и столбцов (column) матрицы. При этом высота столбцов определяется содержимым ячеек матрицы.
Такое построение обеспечивает графическая функция matrixplot из пакета расширения plots. На рис. 13.67 показано совместное применение этой функции с двумя функциями пакета linalg, формирующими две довольно экзотические матрицы А и В.
Рис. 13. 67. Графическое представление матрицы
На рис. 13.67 показана графическая визуализация матрицы, полученной как разность матриц А и В. Для усиления эффекта восприятия применяется цветовая функциональная закраска. Для задания цвета введена процедура F.
Похожие работы
... для работы с графикой. Также на этом же рисунке отображено контекстное меню, появляющееся при щелчке правой кнопкой мыши, когда указатель расположен в области графического вывода. При выделении двумерной графики на рабочем листе меню Insert, Spreadsheet и Options, находящиеся в строке основного меню, заменяются новыми Style, Legend. Axes, Projection, Animation и Export, которые позволяют изменить ...
... Windows будем подразумевать операционные системы Windows 95 и Windows NT, имеющие практически идентичный интерфейс пользователя. С точки зрения работы в них системы MathCAD 7. 0 разницы между этими операционными системами нет. 1. 2. Инсталляция и запуск системы Системы MathCAD 7. 0 PRO поставляются на CD-ROM (возможна поставка минимальных версий и на 3, 5-дюймовых дискетах). При этом полная ...
... размечают в логарифмическом масштабе, где изменение частоты в 10 раз называется декадой, амплитуду откладывают в децибелах и фазу q в градусах. 1.4 Анализ устойчивости непрерывных и дискретных систем Системы стабилизации должны обеспечивать устойчивость и заданную точность регулирования отклонений углов и координат центра масс ЛА от программных значений. При этом могут налагаться ограничения ...
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...
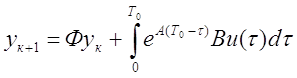
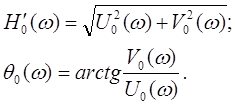
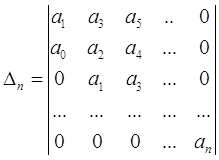
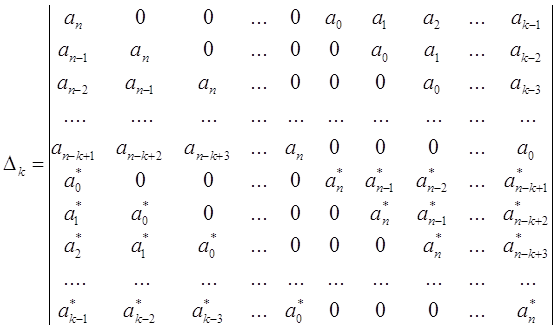
0 комментариев