Визуализация Ньютоновых итераций

13.11.5. Визуализация Ньютоновых итераций

Теперь займемся довольно рискованным экспериментом — наблюдением Ньютоновых итераций с их представлением на комплексной плоскости. На рис. 13.68 задана функция f(z) комплексного аргумента. Для этого используется итерационное выражение. Проследить за поведением функции на комплексной плоскости позволяет графическая функция complexplot3d из пакета plots.

Наблюдаемая картина весьма необычна и свидетельствует о далеко не простом ходе итерационного процесса. Риск работы с этим примером заключается в том, что иногда он ведет к фатальным ошибкам, ведущим к прекращению работы с системой. Обычно при пуске этого примера сразу после загрузки системы Maple V такого не происходит, но когда память загружена другими примерами, сбой

вполне возможен. Рекомендуется записывать подобные примеры на диск перед ик запуском. •

Рис. 13.68. Наблюдение за процессом Ньютоновых итерации в ЗО-пространстве.

13.11.6. Визуализация корней случайных полиномов

Наряду с традиционной для математических и статистических компьютерных систем возможностью генерации случайных чисел, Maple V предоставляет довольно «экзотическую» возможность генерации случайных полиномов с высокой максимальной степенью. Для этого используется функция:

ranpoly(var,o)

Она возвращает случайный полином переменной var, причем максимальная степень полинома птах может указываться опцией о вида degree=nmax.

Приведем пример генерации случайного полинома с максимальной степенью 50:

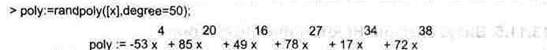
Поскольку полученный полином случайный, то вам не удастся повторить его генерацию — каждый запуск randpoly дает новый полином. Так что важно понять в принципе осуществляемые далее действия. Прежде всего найдем список корней полинома S:

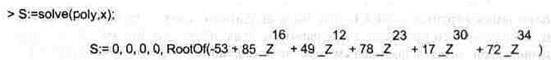
В этом примере обратите внимание на число нулей в начале списка — их надо исключать из дальнейших вычислений. Это, и получение корней в виде обычных

комплексных чисел, делается с помощью функции allvalues, в которой в качестве

параметра надо использовать S[5]. Ниже показано создание списка SA корней полученного выше полинома:

>SA:=[S[1],S[2],S[3],S[4],allvalues(S[5])];

ЗА := [0, 0, 0, 0, -1.010550161 - .1475724933 I,

-1.010550161 + .1475724933 I, -.9465649833,

-.9003773676 - .5534775311 , -.9003773676 + .5534775311 ,

-.8562982808 - .3789548397 , -.8562982808 + .3789548397 ,

-.7320300364 - .6478720727 , -.7320300364 + .6478720727 ,

-.5900687567 - .7989860949 , -.5900687567 + .7989860949 .

-.3987161272-.8962702262 ,-.3987161272 + .8962702262 ,

-.3642724499-.9481481280 ,-.3642724499 + .9481481280 ,

-.02839255705 - .9363196855 I, -.02839255705 + .9363196855 I, .05710128939 -1.018443049 I, .05710128939 + 1.018443049 I, .2868399179-.9808645873 , .2868399179 + .9808645873 , .4149289767-.8396518590 , .4149289767 + .8396518590 , .6775641178-.8099749786 , .6775641178 + .8099749786 , .6864940076 - .6957907203 , .6864940076 + .6957907203 , .8450577013-.4872509104 , .8450577013 + .4872509104 , .9089753119-.3749374155 , .9089753119 + .3749374155 , .9157897832, 1.019132014 - .2114677899I, 1.019132014+.21146778991]

Напоминаем, что эти корни также являются случайными. Теперь можно построить комплексные корни полученного случайного полинома в виде точек на комплексной плоскости:

>with(plots):complexplot(SA,x~1.2..1.2,style=point);

Этот график показан на рис. 13.69.

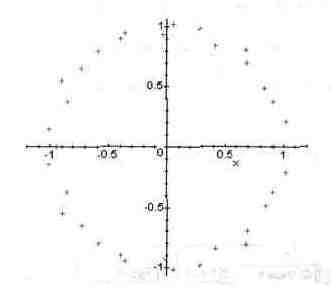
Рис. 13.69. Расположение корней случайного полинома на комплексной плоскости.

Можно заметить любопытную закономерность — точки, представляющие корни случайного полинома укладываются вблизи окружности единичного радиуса с центром в начале координат. Является ли это действительно свойством случайных полиномов или дело в специфике их генерации средствами Maple V — для большинства из нас неясно. Однако этот пример, приводимый в большинстве книг по Maple V, показывает, что порою вычисления могут давать довольно неожидан-

ные результаты. Кстати говоря, аналитически можно вычислять корни полинома с максимальной степенью не более четырех.

Приведенные примеры дают весьма наглядное представление о больших возможностях визуализации решений самых различных задач в системе Maple V. Можно значительно повысить ее, эффектно используя описанные ранее приемы анимации (оживления) изображений. В целом надо отметить, что графические возможности Maple V дают новый уровень качества графики современных математических систем, о котором с десяток лет тому назад можно было только мечтать.

Похожие работы

Двумерная графика системы Maple

Скачать

18394

1

6

... для работы с графикой. Также на этом же рисунке отображено контекстное меню, появляющееся при щелчке правой кнопкой мыши, когда указатель расположен в области графического вывода. При выделении двумерной графики на рабочем листе меню Insert, Spreadsheet и Options, находящиеся в строке основного меню, заменяются новыми Style, Legend. Axes, Projection, Animation и Export, которые позволяют изменить ...

Основы работы с системой MathCAD 7. 0 PRO

Скачать

78056

0

20

... Windows будем подразумевать операционные системы Windows 95 и Windows NT, имеющие практически идентичный интерфейс пользователя. С точки зрения работы в них системы MathCAD 7. 0 разницы между этими операционными системами нет. 1. 2. Инсталляция и запуск системы Системы MathCAD 7. 0 PRO поставляются на CD-ROM (возможна поставка минимальных версий и на 3, 5-дюймовых дискетах). При этом полная ...

Системы стабилизации и ориентации

Скачать

26620

1

17

... размечают в логарифмическом масштабе, где изменение частоты в 10 раз называется декадой, амплитуду  откладывают в децибелах и фазу q в градусах. 1.4 Анализ устойчивости непрерывных и дискретных систем Системы стабилизации должны обеспечивать устойчивость и заданную точность регулирования отклонений углов и координат центра масс ЛА от программных значений. При этом могут налагаться ограничения ...

Вычислительная математика

Скачать

100779

18

23

... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...