Навигация
Графика пакета plots 13.6.1. Общая характеристика пакета plots
13.6. Графика пакета plots 13.6.1. Общая характеристика пакета plots
Пакет plots содержит почти полсотни графических функции, существенно расширяющих возможности графики системы Maple V. В реализации R4 этот пакет содержит следующие функции:
| ——————————— animate | Создает мультипликацию 2D графиков функций. |
| animated | Создает мультипликацию 3D графиков функции. |
| changecoords | Смена системы координат. |
| compiexplot | Построение 20-графика на комплексной плоскости. |
| complexplot3d | Построение 30-графика в комплексном пространстве. |
| conformal | Конформный график комплексной функции. |
| contourplot | Строит координатную систему контурши-м графика. |
| contourplot3d | Строит контурный 30-график. |
| coordplot | Строит координатную систему 20-графиков. |
| coordplotSd | Строит координатную систему ЗО-графиков. |
| cylinderplot | Строит график 3D поверхности в цилиндрических координатах. |
| densityplot | Строит двумерный график плотности. |
| display | Строит график списка графических объектов. |
| display3d | Строит график списка трехмерных графических объектов. |
| fieldplot | Строит график 2D векторного поля. |
| fieldplot3d | Строит график 3D векторного поля. |
| gradplot | Строит график 2D векторного поля градиента. |
| gradplot3d | Строит график 3D векторного поля градиента. |
| implicitplot | Строит 2D-гpaфик неявной функции. |
| implicitplot3d | Строит ЗО-график неявной функции. |
| inequal | Строит график решения системы неравенств. |
| listcontplot | Строит 20-контурный график для сетки значении. |
| listcontplot3d | Строит ЗО-контурныи график для сетки значении. |
| listdensityplot | Строит 20-график плотности для сетки значении. |
| listplot | Строит 20-график для листа значений. |
| listplot3d | Строит ЗО-график для листа значении. |
| loglogplot | Строит логарифмический 20-график функции. |
| logplot | Строит полулогарифмический 2D- график функции. |
| matrixplot | Строит ЗО-график со значениями Z, определенными матрицей. |
| odeplot | Строит 2D или 3D график решения дифференциальных уравнений. |
| pareto | Строит pareto-диаграммы (гистограмма + график линиями). |
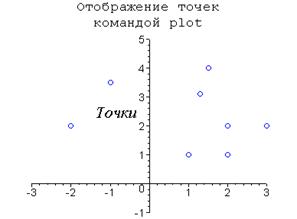
| pointplot | Строит 2D точечный график. |
| pointplot3d | Строит 3D точечный график. |
| polarplot | Строит график 2D кривой в полярной системе координат. |
| polygonplot | Строит график одного или большего количества многоугольников. |
| polygonplot3d | Строит график одного или большего количества многоугольников. |
| polyhedraplot | Строит трехмерный график многогранника. |
| replot | Перестраивает заново график. |
| rootlocus | Строит график корней уравнения с комплексными неизвестными. |
| semilogplot | Строит график функции с логарифмическим масштабом по горизонтали. |
| setoptions | Устанавливает опции по умолчанию для 2D графиков. |
| setoptions3d | Устанавливает опции по умолчанию для 3D графиков. |
| spacecurve | Строит 3D пространственные кривые. |
| sparsematrixplot | Строит ZD-график отличных от нуля значений матрицы. |
| sphereplot | График 3D- поверхности в сферических координатах. |
| surfdata | Строит ЗD-гpaфик поверхности по численным данным. |
| textplot | Выводит на заданное место 2D-гpaфикa текст. |
| textplot3d | Выводит на заданное место ЗD-rpaфикa текст. |
| tubeplot | Строит ЗD-rpaфики типа трубы. |
Среди этих функций надо отметить прежде всего средства построения графиков ряда новых типов (например, в виде линий равного уровня, векторных полей и т.д.), а также средства объединения различных графиков в один. Особый интерес представляют две первые функции, обеспечивающие оживление (анимацию) как двумерных графиков (animate), так и трехмерных (animate3d). Этот пакет вполне
заслуживает описания в отдельной книге. Но, учитывая ограниченный объем данной книги, мы рассмотрим лишь несколько характерных примеров его применения. Заметим, что для использования приведенных функций нужен вызов пакета, например, командой with(plots).
Похожие работы
... для работы с графикой. Также на этом же рисунке отображено контекстное меню, появляющееся при щелчке правой кнопкой мыши, когда указатель расположен в области графического вывода. При выделении двумерной графики на рабочем листе меню Insert, Spreadsheet и Options, находящиеся в строке основного меню, заменяются новыми Style, Legend. Axes, Projection, Animation и Export, которые позволяют изменить ...
... Windows будем подразумевать операционные системы Windows 95 и Windows NT, имеющие практически идентичный интерфейс пользователя. С точки зрения работы в них системы MathCAD 7. 0 разницы между этими операционными системами нет. 1. 2. Инсталляция и запуск системы Системы MathCAD 7. 0 PRO поставляются на CD-ROM (возможна поставка минимальных версий и на 3, 5-дюймовых дискетах). При этом полная ...
... размечают в логарифмическом масштабе, где изменение частоты в 10 раз называется декадой, амплитуду откладывают в децибелах и фазу q в градусах. 1.4 Анализ устойчивости непрерывных и дискретных систем Системы стабилизации должны обеспечивать устойчивость и заданную точность регулирования отклонений углов и координат центра масс ЛА от программных значений. При этом могут налагаться ограничения ...
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...


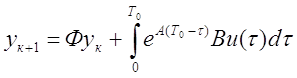
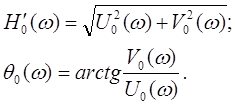
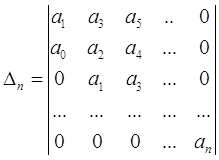

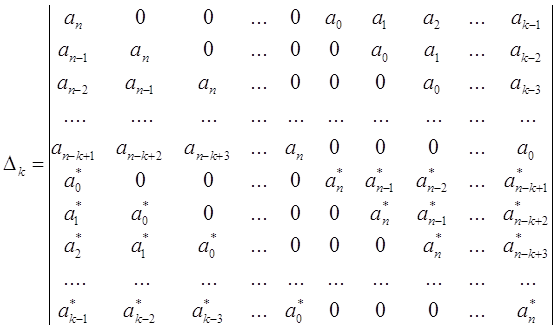
0 комментариев