Задание координатных систем 20-графиков и их пересчет
Графики функций в неограниченном масштабе
Построение графиков функций, заданных их именами
Построение ЗО-графиков с помощью функция plot3d
Примеры построения трехмерных поверхностей с помощью функции plot3d
Задание 30-графики в виде процедуры
Графика пакета plots 13.6.1. Общая характеристика пакета plots
Построение графиков функций в двумерной полярной системе координат
Графики в разных системах координат
Построение анимационных 20-графиков
Графическое представление решений дифференциальных уравнений
Функция DEplot3d из пакета DEtools
Графическая функция phaseportrait
Графическая визуализация решений и анимация
Визуализация Ньютоновых итераций
Анимация разложения импульса в ряд Фурье
Работа с электронными таблицами
Трансформация графиков в реальном масштабе времени
Расширяемое меню справочной системы
Навигация
Построение графиков функций в двумерной полярной системе координат
Графика в системе Maple V
109435
знаков
6
таблиц
96
изображений
13.6.2. Построение графиков функций в двумерной полярной системе координат
В пакете plots есть функция для построения графиков в полярной системе координат. Она имеет вид polarplot(L,o), где L — объекты для задания функции, график которой строится и о — необязательные опции. На рис. 13.27 представлен пример построения графика с помощью функции polarplot.
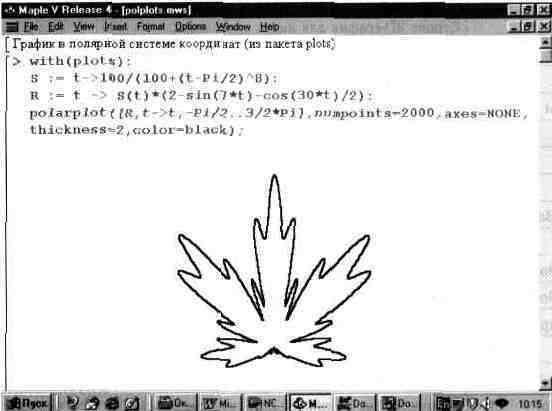
Рис. 13.27. График, построенный с помощью функции polarplot.
В данном случае для большей выразительности опущено построение координатных осей, а график выведен линией удвоенной толщины. График очень напоминает лист клена, весьма почитаемого в Канаде и ставшего эмблемой системы Maple V.
13.6.3. Построение графиков линиями равного уровня
Графики, построенные с помощью линий равного уровня (их также называют контурными графиками) часто используются в картографии. Эти графики получаются, если мысленно провести через трехмерную поверхность ряд равноотстоящих плоскостей, параллельных плоскости, образованной осями Х и Y графика. Линии равных высот образуются в результате пересечения этих плоскостей с трехмерной поверхностью.
Для построения таких графиков используется функция contourplot, которая может использоваться в нескольких форматах:
contourplot(exprl,x=a..b,y=c..d)
contourplot(f,a..b,c..d)
contourplot([ exprf,exprg,exprh ],s=a..b,t=c..d)
contourplot([ f,g,h ],a..b,c..d)
contourplot3d(exprl,x=a..b,y=c..d)
contourplot3d(f,a..b,c..d)
contourplot3d([ exprf,exprg,exprh ],s=a..b,t=c..d) »'
contourplot3d([ f,g,h ],a..b,c..d)
Здесь — f, g и h — функции, expri — выражение, описывающее зависимость высоты поверхности от координат х и у, exprf, exprg и exprh — выражения, зависящие от s и t, описывающие поверхность в параметрической форме, а и b — константы вещественного типа, end — константы или выражения вещественного типа, х, y,,s и t — имена независимых переменных.
На рис. 13.28 показано построение графика линиями равного уровня для одной функции. Опция filled=true обеспечивает автоматическую функциональную окраску замкнутых фигур, образованных линиями равного уровня. Порою это придает графику большую выразительность, чем при построении только линий равного уровня.
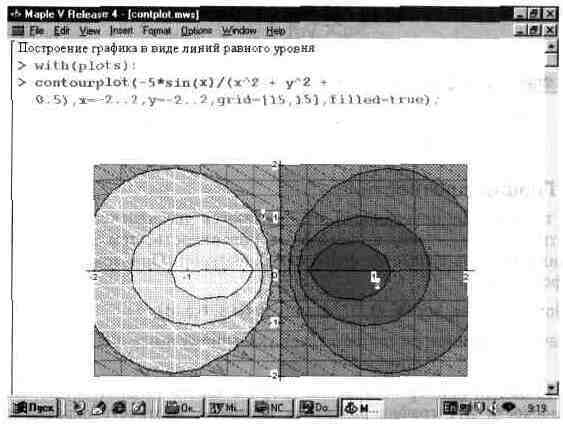
Рис. 13.28. Пример построения графика функции линиями равного уровня.
Функция contourplot позволяет строить и графики ряда функций. Пример такого построения показан на рис. 13.29. Множество окружностей на этом рисунке создается четырьмя поверхностями, заданными функциями с1, с2, сЗ и с4.
Следует отметить, что, хотя графики в виде линий равного уровня выглядят не так эстетично и естественно, как обычные графики трехмерных поверхностей (ибо требуют осмысления результатов), у них есть один существенный плюс — экстремумы функций на таких графиках выявляются порой более четко, чем на обычных графиках. Например, небольшая возвышенность или впадина за большой «горой» на обычном графике может оказаться невидимой, поскольку заслоняется
«горой» — на графике линий равного уровня этого эффекта нет. Однако выразительность таких графиков сильно зависит от числа линий равного уровня.
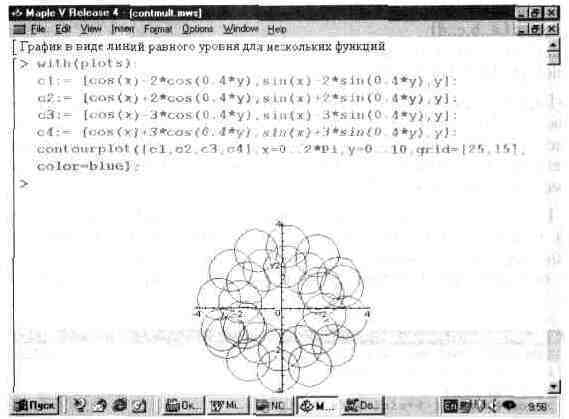
Рис. 13.29. Пример построения графиков многих функций линиями равного уровня.
13.6.4. График плотности
Иногда трехмерные поверхности отображаются на плоскости как графики плотности окраски — чем выше высота поверхности, тем плотнее окраска. Такой вид графиков создается функцией densityplot. Она может записываться в двух форматах:
densityplot(exprl,x=a..b,y=c..d) densityplot(f,a..b,c..d),
где назначение параметров соответствует указанному выше для функции contour-plot.
На рис. 13.30 дан пример построения графика такого типа. Нетрудно заметить, что в плоскости X,Y график разбит на квадраты, плотность окраски которых различна. В нашем случае плотность окраски задается оттенками серого цвета.
Обычно графики такого типа не очень выразительны, но имеют свои области применения. К примеру, оттенки окраски полупрозрачной жидкости могут указывать на рельеф поверхности дна емкости, в которой находится эта жидкость.
13.6.5. График векторного поля двумерный
Еще один распространенный способ представления трехмерных поверхностей — графики векторного поля. Они часто применяются для отображения полей, например, электрических зарядов. Особенность таких графиков в том, что для их построения используют стрелки, направление которых соответствует направлению изменения градиента поля, а длина — значению градиента.
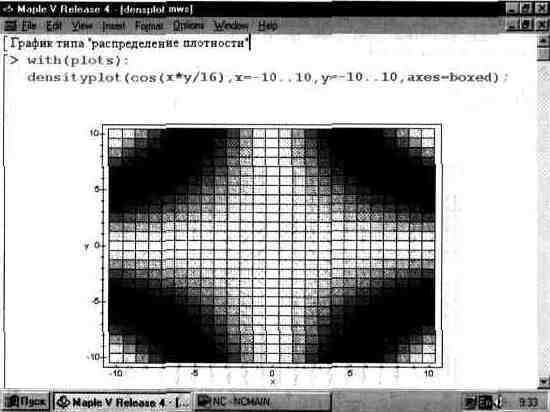
Рис. 13.30. График плотности для заданной функции.
Для построения таких графиков в двумерной системе координат используется функция fieldplot:
fieldplot(f, rl, r2) или fieldplot(f, rl, r2, ...),
где f — вектор или множество векторов, задающих построение, и rl и r2 — пределы.
На рис. 13.31 показан вид одного из таких графиков. Следует отметить, что для получения достаточного числа отчетливо видных стрелок надо поработать с форматированием графиков. Иначе графики этого типа могут оказаться не очень представительными. Так, слишком короткие стрелки превращаются в черточки и даже точки, не имеющие острия, что лишает графики наглядности.
Чуть позже мы рассмотрим построение на одном рисунке графиков плотности и векторного поля, а также создание более наглядных жирных стрелок.
Похожие работы
... для работы с графикой. Также на этом же рисунке отображено контекстное меню, появляющееся при щелчке правой кнопкой мыши, когда указатель расположен в области графического вывода. При выделении двумерной графики на рабочем листе меню Insert, Spreadsheet и Options, находящиеся в строке основного меню, заменяются новыми Style, Legend. Axes, Projection, Animation и Export, которые позволяют изменить ...
... Windows будем подразумевать операционные системы Windows 95 и Windows NT, имеющие практически идентичный интерфейс пользователя. С точки зрения работы в них системы MathCAD 7. 0 разницы между этими операционными системами нет. 1. 2. Инсталляция и запуск системы Системы MathCAD 7. 0 PRO поставляются на CD-ROM (возможна поставка минимальных версий и на 3, 5-дюймовых дискетах). При этом полная ...
... размечают в логарифмическом масштабе, где изменение частоты в 10 раз называется декадой, амплитуду откладывают в децибелах и фазу q в градусах. 1.4 Анализ устойчивости непрерывных и дискретных систем Системы стабилизации должны обеспечивать устойчивость и заданную точность регулирования отклонений углов и координат центра масс ЛА от программных значений. При этом могут налагаться ограничения ...
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...
0 комментариев