Аппроксимация плотности земной атмосферы аналитическими зависимостями

3.2.1.1 Аппроксимация плотности земной атмосферы аналитическими зависимостями

Предполагается, что рассматриваемая модель упругого космического аппарата [1, 3, 10, 11] движется в атмосфере земли. Тогда на КА действуют моменты внешних сил, такие как гравитационный и аэродинамический моменты. Для нахождения аэродинамического момента, необходимо знать плотность атмосферы, которая зависит от высоты полета.

В данной задаче требуется [11, 24] аппроксимировать функцию полиномом 3-его порядка вида:

; (3.14)

Полином (3.14) в каждом из узлов аппроксимации должен удовлетворять условию:

; (3.15)

Таким образом, задача аппроксимации функции сводится к решению системы с N+1 уравнений с тремя неизвестными:

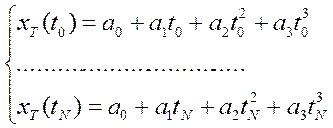; (3.16)

Это объясняется тем, что полином должен пройти через все N+1 точек (в данном случае это 25 точек) в которых задана функция x = x(t).

Метод наименьших квадратов позволяет такую систему привести к решаемой системе. Запишем функционал:

.

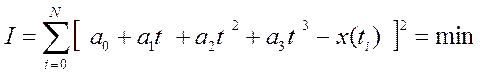Это достигается тогда, когда выполняется:

;

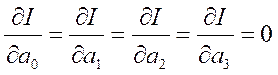Взяв соответствующие производные, получим систему:

;

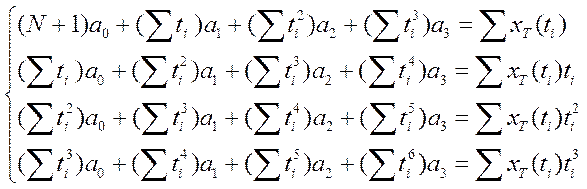(3.17)

В отличии от системы (3.16) полученная система определена и имеет единственное решение [24].

В результате проведенных расчетов, для составления системы, были произведены расчеты, приводить которые нецелесообразно ввиду их громоздкости.

Подставив в систему (3.17) соответствующие значения, в результате мы получим систему. Эту систему будем решать методом Гаусса.

 3.2.1.2 Построение аппроксимирующего полинома для плотности земной атмосферы

Воспользовавшись таблицей стандартной атмосферы [10,11], построим графики зависимостей от высоты функции Po(H):

Плотность:

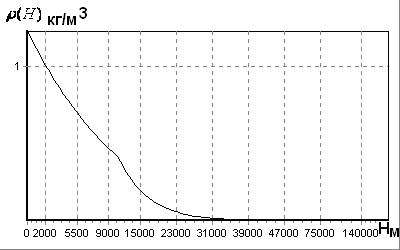
Рис. 3.3 - Зависимость плотности воздуха от высоты

Аппроксимирующий полином:

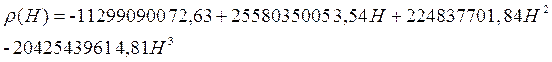
3.2.2 Гравитационный момент

В обычных задачах механики [1, 3, 6, 10, 11, 12], связанных с ее техническими приложениями, ускорения силы тяжести в различных точках материального тела считаются равными как по величине, так и по направлению. Это сразу приводит к известному положению о совпадении центра масс и центра тяжести материального тела и, как следствие, к равенству нулю момента гравитационных сил относительно центра масс. На самом деле векторы ускорения силы тяжести различных точках тела всегда различны, вследствие того, что все они направлены к центру Земли, а, следовательно, если рассматриваемые точки не лежат на одной прямой, проходящей через центр притяжения, то векторы параллельны, а если точки лежат на одной такой прямой, то – имеют различное удаление от центра притяжения и, значит, соответствующие ускорения отличаются по величине. Однако это уточнение в обычных задачах механики несущественно, поскольку размеры технических сооружений малы по сравнению с радиусом Земли, и поэтому вызванные сформулированным здесь уточненные моменты столь малы по сравнению с другими, что учет их не смысла.

Космический аппарат, движущийся по околоземной орбите [6], тоже мал по сравнению с расстоянием до центра притяжения планеты, однако он не подвержен (если не считать времени включения двигателей) действию больших внешних моментов, и поэтому пренебрежение малыми в обычной технике моментами (гравитационными, связанными со световым давлением и т. п.) уже не будет законным без соответствующей оценки этих моментов [1, 3].

Прежде, чем получить формулы для вычисления гравитационных моментов и обсудить некоторые следствия, вызванные существованием этих внешних моментов, поясним физическую сущность рассматриваемого явления па простейшем примере. Пусть в центральном ньютоновом поле сил находится тело, могущее быть представленным в виде двух одинаковых точечных масс, соединенных невесомым стержнем (идеализированная гантель), и пусть этот стержень будет наклонен на некоторый угол (отличный от 0 и pi/2) к линии, соединяющей его середину А с центром притяжения С (рис. 3.4).

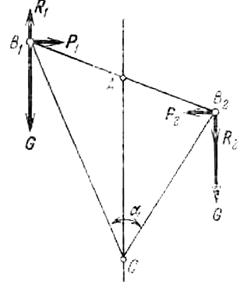
Рис. 3.4 – Тело в виде двух одинаковых точечных масс, соединенных невесомым стержнем (идеализированная гантель) в ньютоновом поле

Если принять обычные допущения о параллельности и равенстве сил тяжести) действующих на обе массы гантели (считаем, что на них действует ускорение силы тяжести, соответствующее точке А), то связанные с ними силы G не дали бы момента относительно точки А, являющейся центром масс рассматриваемого тела. На самом деле силы тяжести будут действовать по прямым В1С и В2С, а величина силы тяжести в точке И1 будет меньше, чем в точке И2, поскольку В1С > В2С. Поэтому к “обычным” силам G, вычисленным по вектору ускорения силы тяжести, соответствующему точке А, следует ввести поправки, например малые силы P1i и P2, изменяющие должным образом величины сил тяжести, действующий на материальные точки, и силы P1 и Р2, изменяющие должным образом направления этих сил тяжести. Из рисунка видно, что пара сил R1 и R2 и пара сил P1 и Р2 (их можно считать 'парами, постольку малые силы Р1 и Р2, а также R1 и R2 будут отличаться друг от друга на .величины высшего порядка малости) создают моменты одного знака, стремящиеся совместить ось тела B1B2 с исправлением АС.

Таким образом, как зависимость величины ускорения силы тяжести от расстояния до центра притяжения, так и центральность поля тяготения приводят к эффектам одного типа - к появлению моментов, стремящихся повернуть ось тела, связанную с геометрией распределения масс в нем, в некоторое определенное положение относительно прямой, соединяющей центр масс тела с центром притяжения.

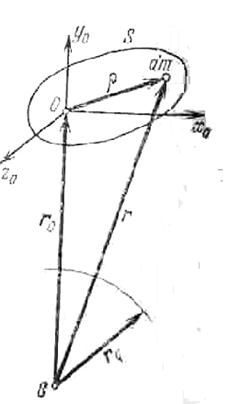
Рис. 3.5.

Найдем выражения, позволяющие вычислять составляющие вектора гравитационного момента Мгр, действующего на некоторое тело S [1, 3]. Введем связанную с телом правую систему координат ОXоYоZo с ортами i, j, k и началом в центре масс тела О, которая совпадает с орбитальной. Соответственно ось OYo натравим по продолжению радиуса-вектора, соединяющего центр притяжения С с началом О, а ось ОXo расположим в мгновенной орбитальной плоскости. Гравитационный момент, действующий на тело S, будет равен:

;

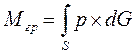где p - радиус-вектор некоторой элементарной массы материального тела,

dG-вектор силы тяжести, действующей на эту элементарную массу. Очевидно, что

.

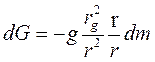Здесь g - ускорение силы тяжести на поверхности планеты, r – радиус-вектор элементарной массы dm относительно центра тяготения С, гg -удаление поверхности планеты от центра C. Введя еще r0 - радиус-вектор центра масс тела S относительно С, следовательно [3]:

;

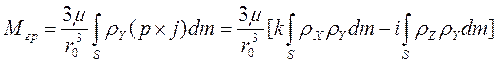где  - гравитационная постоянная для рассматриваемой планеты, равная .

Проекции гравитационного момента на оси триэдра ОXoYoZo, будут равны:

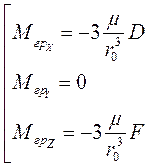; (3.18)

где D и F-центробежные моменты инерции тела S, определяемые для системы

осей ОXоYоZo.

Полученные для гравитационного момента выражения говорят о том, что вектор этого момента всегда лежит в плоскости местного горизонта (перпендикулярен к местной вертикали СО) [1, 4, 10]. Кроме того, очевидно, что гравитационный момент для тела, главные центральные оси инерции которого в данное мгновение совпадают с орбитальными, равен нулю (так как в этом случае D=F=0), в частности он всегда равен нулю для тела, эллипсоид инерции которого является сферой.

В общем случае главные центральные оси инерции тела могут быть повернуты произвольным образом относительно орбитальных осей ориентации. Обозначим жестко связанный с телом S триэдр, совпадающий с главными центральными осями инерции, через Охуz, а для орбитальных осей сохраним обозначение OXoYoZo. Взаимное положение этих систем координат определим следующей таблицей направляющих косинусов:

.

Найдем проекцию гравитационного момента на ось Ох. Очевидно, что

. (3.19)

Воспользовавшись свойством направляющих косинусов, преобразуем равенство (3.19) с учетом формул (3.18):

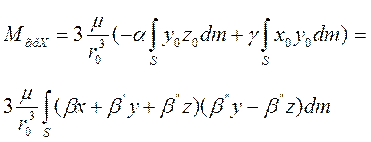; (3.20)

поскольку триэдр Oxyz совпадает с главными центральными осями инерции, постольку все центробежные моменты инерции в этих осях будут равны нулю, и выражение (3.20) может быть упрощено [1, 3]. Проделав аналогичные выкладки для нахождения проекций гравитационного момента можно, написать:

(3.21)

Таким образом, гравитационный момент, действующий вокруг одной из осей триэдра Oxyz, зависит от разности моментов инерции относительно двух других осей. Чтобы сделать анализ полученных выражений более наглядным, рассмотрим гравитационный момент, действующий на тело S, при условии, что оси 0Z и 0Zo совпадают. Это соответствует повороту тела S, который можно назвать поворотом по тангажу, на угол  (рис. 3.6).

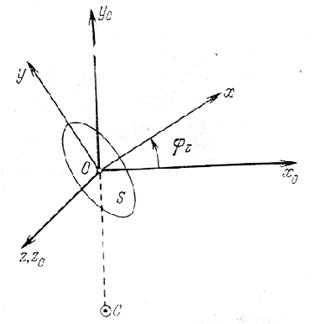
Рис. 3.6 - Поворот тела вокруг оси Z

При сделанных предположениях

,  ;

н, следовательно,

 ;

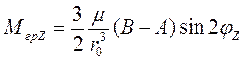Как и надо было ожидать, при  гравитационный момент обращается в нуль, поскольку триэдры Охуz и 0XoYoZo в этом случае совпадают [1, 3]. При монотонном увеличении  от  гравитационный момент возрастает, достигает максимума при , затем убывает и вновь становится равным нулю при . Таким образом, существует два положения равновесия: при  и при . Однако, из этих положений одно соответствует статической устойчивости (при малом изменении , возникает момент противоположного знака), другое – статистической неустойчивости. Действительно, производная

;

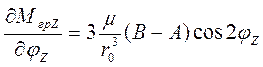при  и при  имеет разные знаки. Какое из этих двух положений соответствует статистической устойчивости, зависит от знака (B-A) [1, 3, 8]. Условие устойчивости (возникновение восстанавливающего момента при малом отклонении)  реализуется при  для A>B или при  для B>A, т.е. в обоих случаях вытянутая ось тела должна занимать вертикальное положение.

Таким образом, вытянутое в вертикальном положении тело, обладая статистической устойчивостью по тангажу и крену, является нейтральным по отношению к углу рыскания [1, 3, 4].

Похожие работы

Совершенствование системы управления персоналом (на примере службы ЭРТОС ООО "Информ-Сервис" филиала "Аэронавигация Центральной Волги" ФГУП "Госкорпорация по ОрВД")

Скачать

126288

13

18

... удостоверение установленной формы. 3.         Предложения по повышению эффективности системы управления персоналом в службе ЭРТОС филиала «Аэронавигация Центральной Волги» ФГУП «Госкорпорация по ОрВД» Анализ существующей системы управления персоналом в службе ЭРТОС показал, что требуется совершенствование существующей системы оплаты труда, необходимо уделить внимание подготовке кадрового ...

Управление фирмой в условиях рынка

Скачать

64530

1

4

... определенной долей государственного регулирования, направленного на достижение оптимального соотношения притязаний предпринимателя в его деятельности по получению прибыли и принципа общественной справедливости. 2.2.Проблемы управления фирмой в условиях рынка При переходе к рыночной экономике предприятия России столкнулись с массой проблем, решить которые все разом оказалось большинству из них ...

Буран

Скачать

107300

23

17

... техника одержали новую выдающуюся победу, Успешно выполнен испытательный запуск универсальной ракетно-космической транспортной системы "Энергия" и орбитального корабля "Буран". Подтверждены правильность принятых инженерных и конструкторских решений, эффективность методов экспериментальной отработки и высокая надежность всех систем этого сложнейшего ...

Разработка отказоустойчивой операционной системы реального времени для вычислительных систем с максимальным рангом отказоустойчивости

Скачать

148576

34

0

... элементов, глобальное пространство имен, а также лавинообразную первоначальную загрузку сети. Таким образом ОСРВ SPOX имеет необходимые механизмы для создания отказоустойчивой распределенной операционной системы реального времени, концепция построения которой описана в главе 2. 4.3 Аппаратно-зависимые компоненты ОСРВ Модули маршрутизации, реконфигурации, голосования реализованы как аппаратно- ...