Навигация
Решение задачи идентификации отказов
4.5 Решение задачи идентификации отказов
Алгоритм обработки данных в бесплатформенной инерциальной навигационной системе строится с использованием субоптимального дискретного фильтра Калмана [7, 16, 22, 25, 27].
Для малых угловых отклонений осей ССК от БСК и при условии Ix» Iy» Iz уравнения (1.1) и (1.2) запишем в виде [25]:
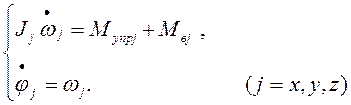
Тогда для построения системы оценки вектора состояния (jj, wj, mвj) примем следующую модель объекта наблюдения [16, 22, 27]:
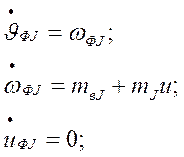 (4.32)
(4.32)
где mj=МДСj/Jj - эффективность управляющего момента;
МДСj - управляющий момент ДС;
mвj=Мвj/Jj - эффективность возмущающего момента;
uj - сигнал управления ДС;
j=x, y, z.
Запишем систему уравнений (4.32) в стандартной векторно-матричной форме, дополнив ее уравнением измерений [7]:
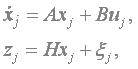
где xj = (x1j, x2j, x3j)T=(jj, wj, mвj)T - вектор состояния;
zj - вектор измерений;
xj - шум измерений;
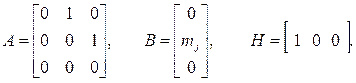 ,
,
j=x, y, z.
Используя критерий Калмана, несложно показать, что такая система является полностью наблюдаема [7, 16, 22, 25, 26, 27]:
rank[HT ATHT (AT)2HT]=n=3, где n - порядок системы.
Реализация в бортовом вычислителе дискретного фильтра Калмана сводится к оценке вектора состояния по следующим соотношениям [25, 27]:
![]()
![]() (4.33)
(4.33)
![]()
![]()
где: ![]() - оценка вектора состояния;
- оценка вектора состояния;
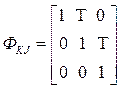 - переходная матрица для вектора состояния;
- переходная матрица для вектора состояния;
![]() - матрица измерений;
- матрица измерений;
![]() - ковариационная матрица ошибок фильтрации;
- ковариационная матрица ошибок фильтрации;
![]() - ковариационная матрица ошибок прогноза;
- ковариационная матрица ошибок прогноза;
![]() - матричный коэффициент усиления;
- матричный коэффициент усиления;
![]() - ковариационная матрица шумов измерения;
- ковариационная матрица шумов измерения;
j=x, y, z.
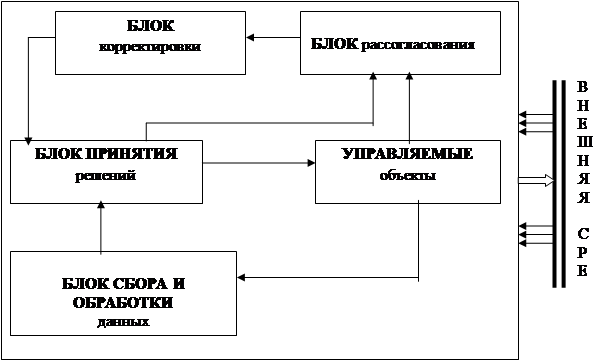
Работа алгоритма основана на анализе величины оцениваемого в фильтре Калмана возмущающего момента [25]. Если математическое ожидание оценки возмущающего момента, вычисленного на некоторой временной базе, где управление равно нулю, превосходит допустимый порог, то принимается решение об отказе ДС и переходе на резерв (рис. 4.7) [25].
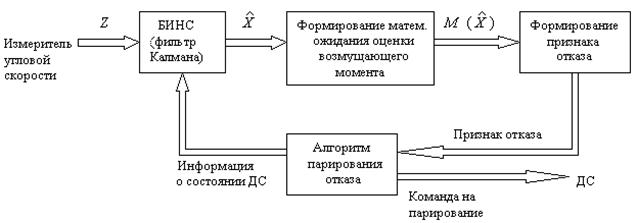
Рис. 4.7 - Обобщенная структурная схема алгоритма
4.6 Метод статистически гипотез
Статистическая гипотеза - есть некоторое предположение относительно свойств [27, 28] генеральной совокупности, из которой извлекается выборка. Критерий статистической гипотезы – это правила позволяющие принять или отвергнуть данную гипотезу на основании выборки. При построении такого правила используются определенные функции результатов наблюдений ![]() ,
называемые статическими для проверки гипотез. Все возможные значения подобных статистик делятся на две части: если нет – гипотеза принимается, как не противоречащая результатам наблюдения, если да – гипотеза отвергается [27, 28, 29]. При этом всегда возможно совершить ошибку; различные типы возможных ошибок заданы в таблице 4.1:
,
называемые статическими для проверки гипотез. Все возможные значения подобных статистик делятся на две части: если нет – гипотеза принимается, как не противоречащая результатам наблюдения, если да – гипотеза отвергается [27, 28, 29]. При этом всегда возможно совершить ошибку; различные типы возможных ошибок заданы в таблице 4.1:
Таблица 4.1
| Гипотеза | Объективно верна | Объективно неверна |
| Принимается | Правильное решение | Ошибка ll рода |
| Отвергается | Ошибка l рода | Правильное решение |
Вероятность совершить ошибку l рода [8] называется уровнем значимости критерия и обозначается q. Обычно уровень значимости выбирают, равным 0.01; 0.1; 0.05 (последнее значение - наиболее часто) [28].
Критерии значимости – это критерии, с помощью которых проверяют гипотезы об абсолютных значениях параметров или о соотношениях между ними для генеральных совокупностей (с точностью до параметров) функцией распределения вероятностей [29].
Построение гистограммы выборки. Гистограмма ![]() является эмпирическим аналогом функции плотности распределения f(x). Обычно ее строят следующим образом:
является эмпирическим аналогом функции плотности распределения f(x). Обычно ее строят следующим образом:
1. Находят предварительное количество квантов (интервалов), на которое должна быть разбита ось Ox. Это количество K определяют с помощью оценочной формулы:
K=1+3.2lgN ; (4.34)
Где найденное значение округляют до ближайшего целого числа.
2. Определяют длину интервала [29]:
![]() ;
(4.35)
;
(4.35)
Величину ![]() можно округлить для удобства вычислений.
можно округлить для удобства вычислений.
3. Середину области изменения выборки (центр распределения) ![]() принимают за центр некоторого интервала, после чего легко находят границы и окончательное количество указанных интервалов так, чтобы в совокупности они перекрывали всю область от
принимают за центр некоторого интервала, после чего легко находят границы и окончательное количество указанных интервалов так, чтобы в совокупности они перекрывали всю область от ![]() до
до ![]() .
.
4. Подсчитывают количество наблюдений ![]() попавшее в каждый квант;
попавшее в каждый квант; ![]() равно числу членов вариационного ряда, для которого справедливо неравенство [27-29]:
равно числу членов вариационного ряда, для которого справедливо неравенство [27-29]:
![]() ; (4.36)
; (4.36)
здесь ![]() и
и ![]() - границы m-ого интервала. Отметим, что при использовании формулы (4.36) значения
- границы m-ого интервала. Отметим, что при использовании формулы (4.36) значения ![]() попавшее на границу между
(m-1)-м и m-ом интервалами, относят к m-ому интервалу.
попавшее на границу между
(m-1)-м и m-ом интервалами, относят к m-ому интервалу.
5. Подсчитывают относительное количество (относительную частоту) наблюдений ![]() /N , попавших в данный квант.
/N , попавших в данный квант.
Строят гистограмму [7, 8, 9], представляющую собой ступенчатую кривую, значения которой на m-ом интервале ![]() , (m=1,2,…,K)
, (m=1,2,…,K)
6. постоянно и равно ![]() /N, или с учетом условия
/N, или с учетом условия 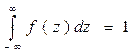 равно (
равно (![]() /N)
/N)![]() .
.
Критерии согласия. Критерием согласия [8] называется критерий гипотезы о том, что генеральная совокупность имеет распределение предполагаемого типа (например, нормально распределение). Среди различных критериев согласия наиболее употребителен универсальный критерий согласия ![]() (Пирсона).
(Пирсона).
Проверку гипотезы о виде функции распределения с помощью этого критерия производят следующим образом [27-29]:
1. a) По выборке строят гистограмму. Если в каком-либо f-ом интервале число наблюдений ![]() окажется меньше пяти, то его объединяют с соседним интервалом (или интервалами) так, чтобы число наблюдений в таком объединенном интервале оказалось большим или равным пяти. Пусть
окажется меньше пяти, то его объединяют с соседним интервалом (или интервалами) так, чтобы число наблюдений в таком объединенном интервале оказалось большим или равным пяти. Пусть ![]() – окончательное число интервала группирования, тогда очевидно, что
– окончательное число интервала группирования, тогда очевидно, что
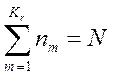 ; (4.37)
; (4.37)
б) Задаются видом гипотетической функции распределения и для каждого из r (r=1,2,…) параметров этого распределения находят оценки, причем эти оценки можно определять как по исходным, так и по сгруппированным данным [27].
в) Определяют теоретическую вероятность ![]() попадания в каждый из
попадания в каждый из ![]() интервалов случайной величины с заданным распределением, параметры которого или известны или оценены в параграфе б) [28].
интервалов случайной величины с заданным распределением, параметры которого или известны или оценены в параграфе б) [28].
г) вычисляют число g:
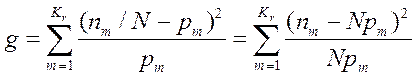 ; (4.38)
; (4.38)
2. Известно, что для данного критерия согласия случайная величина g при Больших N
имеет ![]() распределение с
распределение с ![]() - r - 1 степенями свободы, где r - число определенных неизвестных заранее параметров гипотетического распределения, а уменьшения числа степеней свободы еще на единицу объясняется наличием линейного соотношения (4.35) между эмпирическими величинами
- r - 1 степенями свободы, где r - число определенных неизвестных заранее параметров гипотетического распределения, а уменьшения числа степеней свободы еще на единицу объясняется наличием линейного соотношения (4.35) между эмпирическими величинами ![]() и N , входящими в расчетную формулу (4.36). Задавшись уравнением значимости q, по таблице
и N , входящими в расчетную формулу (4.36). Задавшись уравнением значимости q, по таблице ![]() -распределений находят критическое значение
-распределений находят критическое значение ![]() , причем критическая область определяется неравенством g>
, причем критическая область определяется неравенством g>![]() =
=![]() =
=![]() - r – 1;
- r – 1;![]() .
.
3.Сравнивая значения g и ![]() и выносят решение о принятии (g <=
и выносят решение о принятии (g <=![]() )
или отклонение (g >
)
или отклонение (g >![]() )
рассматриваемой гипотезы о виде функции распределения [27-29].
)
рассматриваемой гипотезы о виде функции распределения [27-29].
Похожие работы
... удостоверение установленной формы. 3. Предложения по повышению эффективности системы управления персоналом в службе ЭРТОС филиала «Аэронавигация Центральной Волги» ФГУП «Госкорпорация по ОрВД» Анализ существующей системы управления персоналом в службе ЭРТОС показал, что требуется совершенствование существующей системы оплаты труда, необходимо уделить внимание подготовке кадрового ...
... определенной долей государственного регулирования, направленного на достижение оптимального соотношения притязаний предпринимателя в его деятельности по получению прибыли и принципа общественной справедливости. 2.2.Проблемы управления фирмой в условиях рынка При переходе к рыночной экономике предприятия России столкнулись с массой проблем, решить которые все разом оказалось большинству из них ...
... техника одержали новую выдающуюся победу, Успешно выполнен испытательный запуск универсальной ракетно-космической транспортной системы "Энергия" и орбитального корабля "Буран". Подтверждены правильность принятых инженерных и конструкторских решений, эффективность методов экспериментальной отработки и высокая надежность всех систем этого сложнейшего ...
... элементов, глобальное пространство имен, а также лавинообразную первоначальную загрузку сети. Таким образом ОСРВ SPOX имеет необходимые механизмы для создания отказоустойчивой распределенной операционной системы реального времени, концепция построения которой описана в главе 2. 4.3 Аппаратно-зависимые компоненты ОСРВ Модули маршрутизации, реконфигурации, голосования реализованы как аппаратно- ...






0 комментариев