Навигация
Основные свойства интеграла
3. Основные свойства интеграла
В этом параграфе мы установим ряд свойств интеграла от ограниченной измеримой функции.
Теорема 1. Если измеримая функция f(x) на измеримом множестве Е удовлетворяет неравенствам a £ f(x) £ b, то
a× mE £ ![]() £ b× mE.
£ b× mE.
Это теорема обычно называется теоремой о среднем.
Доказательство. Пусть n натуральное число. Если мы положим
A = a - ![]() , B = b +
, B = b + ![]() ,
,
то окажется, что
A < f(x) < B,
и суммы Лебега можно будет составлять, дробя сегмент [А, В].
Но еслиA £ yk £ B, то, очевидно,
A![]() £
£ ![]() £ B
£ B![]()
или, что то же самое,
A× mE £ s £ B× mE,
откуда и в пределе
![]() mE £
mE £ ![]() £
£ ![]() mE.
mE.
В силу произвольности числа n, теорема доказана.
Из этой теоремы вытекает несколько простых следствий.
Следствие 1. Если функция f(x) постоянна на измеримом множестве Е и f(x) = с, то
![]() = c× mE.
= c× mE.
Следствие 2. Если функция f(x) не отрицательна (не положительна), то таков же и ее интеграл.
Следствие 3. Если тЕ = 0, то для любой ограниченной функции f(x), заданной на множестве Е, будет
![]() = 0.
= 0.
Теорема 2. Пусть на измеримом множестве Е задана измеримая ограниченная функция f(x). Если множество Е есть сумма конечного числа или счетного множества попарно не пересекающихся измеримых множеств
E =![]() (Ek
(Ek![]() = 0, k ¹ k’),
= 0, k ¹ k’),
то
![]() =
=![]()
Свойство интеграла, выражаемое этой теоремой, называется его полной аддитивностью.
Доказательство. Рассмотрим сначала простейший случай, когда число слагаемых равно двум
Е = ![]() +
+ ![]() (
(![]()
![]() = 0).
= 0).
Если на множестве Е
A < f(x) < B
и мы, раздробив сегмент [А, В] точками у0, y1,¼ , уn, составим множества
ek = E(yk £ f < yk+1),
ek’= E’(yk £ f < yk+1),
ek’’= E’’(yk £ f < yk+1),
то, очевидно, будем иметь
ek = ek’ + ek’’ (ek’ek’’ = 0),
откуда
![]() =
=![]() +
+ ![]()
н в пределе, при l ® 0,
![]() =
= ![]() +
+ ![]()
Итак, теорема доказана для случая двух слагаемых множеств. Пользуясь методом математической индукции, мы легко распространим теорему на случай любого конечного числа слагаемых множеств.
Остается рассмотреть случай, когда
E = ![]() .
.
В этом случае
![]() = mE,
= mE,
так что при n ® ¥ будет
![]() ® 0.
(*)
® 0.
(*)
Заметив это, положим
![]() = Rn.
= Rn.
Так как для конечного числа слагаемых множеств теорема уже доказана, то
![]() =
= ![]() +
+ ![]() .
.
В силу теоремы о среднем
A× mRn £ ![]() £ B× mRn,
£ B× mRn,
а в силу (*) мера mRn множества Rn стремится к нулю с возрастанием n, откуда ясно, что
![]() ® 0.
® 0.
Но это и означает, что
![]() =
=![]()
Из этой теоремы вытекает ряд следствий.
Следствие 1. Если измеримые ограниченные функции f(x) и g(x), заданные на множестве Е, эквивалентны между собой, то
![]() =
=![]() .
.
Действительно, если
А = Е(f ¹ g), B = E(f = g),
то mA = 0 и
![]() =
= ![]() = 0.
= 0.
На множестве же В обе функции тождественны и
![]() =
= ![]() .
.
Остается сложить это равенство с предыдущим.
В частности, интеграл от функции, эквивалентной нулю, равен нулю.
Само собою разумеется, что последнее утверждение необратимо. Например, если f(x) задана на сегменте [-1, +1], так:
Похожие работы
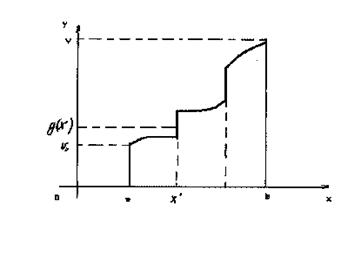
... 2.6 Приведение интеграла Стилтьеса к интегралу Римана Пусть функция непрерывна в промежутке , а монотонно возрастает в этом промежутке, и притом в строгом смысле. Тогда, как показал Лебег, интеграл Стилтьеса с помощью подстановки непосредственно приводится к интегралу Римана. На рисунке изображен график функции . Для тех значений , при которых функция испытывает скачок (ибо мы вовсе ...
... функции стремятся к нулю при . Если соотношение (7) имеет место для всякой суммируемой на [a, b] функции f (t), то мы будем говорить, что последовательность слабо сходится к нулю. §2. Представление функции сингулярным интегралом в заданной точке Во всем дальнейшем будем считать, что ядро при фиксированных n и x ограничено. Тогда сингулярный интеграл имеет смысл при любой ...
... и в том случае, когда интегральный оператор (3) действует в пространстве C(W) и неразложим в этом пространстве относительно конуса неотрицательных функций пространства C(W). Получению оценок спектрального радиуса положительного оператора по информации о поведении этого оператора на фиксированном ненулевом элементе конуса посвящена достаточно обширная литература [21], [11], [13], [18], [26], ...
... интегралы всех разрывных функций, которые можно было построить известными в то время методами (интеграл Лебега). Триумф идей Лебега привел к тому, что даже один из вождей математиков – классиков Гастон Дарбу изменил свое мнение и, выступая в 1908г. на Математическом конгрессе в Риме, говорил о пламенном и пытливом духе математики ХХ в., о науке, ведущей свои изыскания в абсолютно новой области с ...
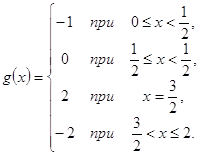
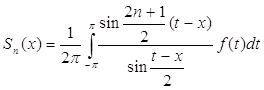
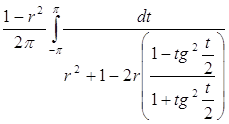
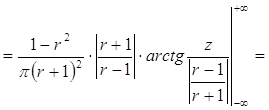
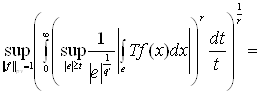
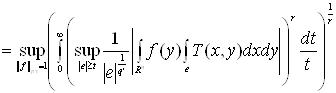
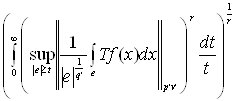
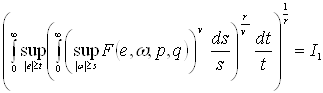



0 комментариев