Навигация
6. Примеры
1) Вычислить интеграл Лебега от функции ![]() на интервале (1; 2).
на интервале (1; 2).
Строим срезку
![]()
N, f(x) ³ N,
fN(x) =
f(x), f(x) < N.
![]() = N,
= N,
x = 1 + ![]() .
.
![]()
![]() =
= ![]() ,
,
![]() =
= ![]() +
+ 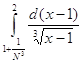 = Nx
= Nx![]() +
+ 
![]() = N
= N![]() - N +
- N + ![]() -
-
- ![]()
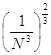 =
= ![]() +
+ ![]() -
- ![]()
![]() = -
= - ![]()
![]() +
+ ![]() ,
,
![]()
![]() =
= ![]()
![]() =
= ![]() ,
,
(L)![]() =
= ![]() .
.
2) Суммируемы ли функции ![]() и
и ![]() на интервале (0; 1).
на интервале (0; 1).
f(x) = ![]() .
.
Строим срезку
![]() = N,
= N,
x = ![]() .
.
![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() = 1 -
= 1 - ![]() = 1 +
= 1 + ![]() ,
,
![]() =
= ![]()
![]() =
= ![]() (1 +
(1 + ![]() ) = +¥,
) = +¥,
значит функция f(x) = ![]() суммируемой не является.
суммируемой не является.
f(x) = ![]() .
.
Строим срезку
![]() = N,
= N,
x = ![]() .
.
![]() =
= ![]() +
+ 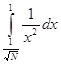 =
= ![]() -
- ![]() =
= ![]() - (1 -
- (1 - ![]() ) =
) = ![]() - 1 +
- 1 + ![]() =
=
= 2![]() - 1,
- 1,
![]() =
= ![]()
![]() =
= ![]() (2
(2![]() - 1) = +¥,
- 1) = +¥,
значит функция f(x) = ![]() суммируемой не является.
суммируемой не является.
3) Суммируема ли функция f(x) = ![]() на отрезке [-1; 1], где f(0) = 0.
на отрезке [-1; 1], где f(0) = 0.
![]()
![]()
![]() , x > 0 0 , x ³ 0
, x > 0 0 , x ³ 0
![]() =
= ![]() =
=
0 , x £ 0 ![]() , x < 0
, x < 0
![]() =
= ![]() -
- ![]() .
.
Строим срезку
N = ![]() ,
,
x = ![]() .
.
(L)![]() =
= ![]()
 =
= ![]()
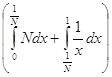 =
= ![]()
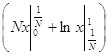 =
=
= ![]()
![]() =
= ![]()
![]() = +¥.
= +¥.
Строим срезку
N = ![]() ,
,
x = ![]() .
.
(L)![]() =
= ![]()
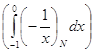 =
= ![]()
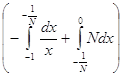 =
= ![]()
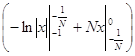 =
=
= ![]()
![]() =
= ![]()
![]() = +¥,
= +¥,
значит функция f(x) = ![]() не является суммируемой на [-1 ;1].
не является суммируемой на [-1 ;1].
4) Суммируема ли функция f(x) = ![]() на [1; 3], где f(2) = 1.
на [1; 3], где f(2) = 1.
![]()
![]()
![]() , x > 2 0, x ³ 2
, x > 2 0, x ³ 2
![]() = 0, x < 2
= 0, x < 2 ![]() =
=
1, x = 2 ![]() , x < 2
, x < 2
Строим срезку
![]() = N,
= N,
x = 2 + ![]() .
.
(L)![]() =
= ![]()
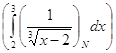 =
= ![]()
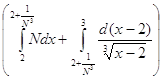 =
=
= ![]()
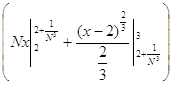 =
= ![]()
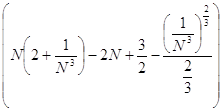 =
=
= ![]()
![]() =
=![]()
![]() =
= ![]() .
.
Строим срезку
![]() = N,
= N,
x = 2 - ![]() .
.
(L)![]() =
= ![]()
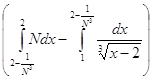 =
= ![]()
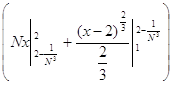 =
= ![]()
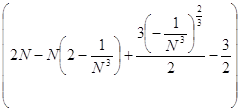 =
= ![]()
![]() =
= ![]()
функция f(x) суммируема на [1; 3].
7. Литература
1) Колмогоров, Фомин «Элементы функционального анализа».
2) Натансон И. П. «Теория функций вещественной переменной», С-П, 1999.
3) Очан «Сборник задач по математическому анализу».
Похожие работы
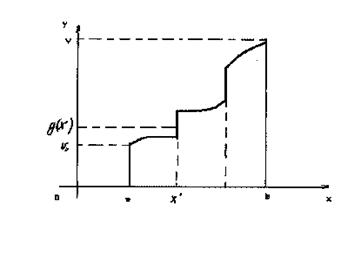
... 2.6 Приведение интеграла Стилтьеса к интегралу Римана Пусть функция непрерывна в промежутке , а монотонно возрастает в этом промежутке, и притом в строгом смысле. Тогда, как показал Лебег, интеграл Стилтьеса с помощью подстановки непосредственно приводится к интегралу Римана. На рисунке изображен график функции . Для тех значений , при которых функция испытывает скачок (ибо мы вовсе ...
... функции стремятся к нулю при . Если соотношение (7) имеет место для всякой суммируемой на [a, b] функции f (t), то мы будем говорить, что последовательность слабо сходится к нулю. §2. Представление функции сингулярным интегралом в заданной точке Во всем дальнейшем будем считать, что ядро при фиксированных n и x ограничено. Тогда сингулярный интеграл имеет смысл при любой ...
... и в том случае, когда интегральный оператор (3) действует в пространстве C(W) и неразложим в этом пространстве относительно конуса неотрицательных функций пространства C(W). Получению оценок спектрального радиуса положительного оператора по информации о поведении этого оператора на фиксированном ненулевом элементе конуса посвящена достаточно обширная литература [21], [11], [13], [18], [26], ...
... интегралы всех разрывных функций, которые можно было построить известными в то время методами (интеграл Лебега). Триумф идей Лебега привел к тому, что даже один из вождей математиков – классиков Гастон Дарбу изменил свое мнение и, выступая в 1908г. на Математическом конгрессе в Риме, говорил о пламенном и пытливом духе математики ХХ в., о науке, ведущей свои изыскания в абсолютно новой области с ...
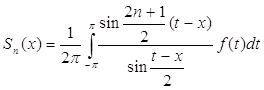



0 комментариев