Навигация
1 при x ³ 0, f(x) =
-1 при x < 0,
то
=
+
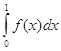= -1 + 1 = 0,
хотя функция f(x) и не эквивалентна нулю.
Однако справедливо
Следствие 2. Если интеграл от неотрицательной измеримой ограниченной функции f(x) равен нулю
(f(x) ³ 0),
то эта функция эквивалентна нулю.
В самом деле, легко видеть, что
E(f>0) = 
.
Если бы f(x) не была эквивалентна нулю, то необходимо нашлось бы такое n0, что
mE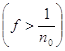
= s > 0.
Полагая
A = E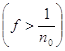, B = B - A,
мы имели бы, что
³ 
s, 
³ 0,
и, складывая эти неравенства, мы получили бы
³ s,
что противоречит условию.
Теорема 3. Если на измеримом множестве Q заданы две измеримые ограниченные функции f(x) и F(x), то
= 
+ 
.
Теорема 4. Если на измеримом множестве Е задана измеримая ограниченная функция f(x) и с есть конечная постоянная, то
= c.
Следствие. Если f(x) и F(х) измеримы и ограничены на множестве Е, то
= 
-.
Теорема 5. Пусть f(x) и F(х) измеримы и ограничены на измеримом множестве Е. Если
f(x) £ F(x),
то
£ .
Действительно, функция F(x)—f(x) не отрицательна, так что
- 
= 
³ 0.
Теорема 6. Если функция f(x) измерима и ограничена на измеримом множестве E, то
£ 
4. Предельный переход под знаком интеграла
Здесь мы рассмотрим следующий вопрос: пусть на измеримом множестве E задана последовательность измеримых ограниченных функций
f1(x), f2(x), f3(x), ¼ , fn(x), ¼
которая в каком-нибудь смысле (везде, почти везде, по мере) сходится к измеримой ограниченной функции F(x). Спрашивается, будет ли справедливо соотношение
= 
(1)
Если (1) верно, то говорят, что допустим предельный переход под знаком интеграла.
Легко видеть, что, вообще говоря, это не так. Например, если функции fn(x) определены в сегменте [0, 1] следующим образом:
n при xÎ 
,
fn(x) =
0 при x 
,
то при всяком x Î [0, 1] будет
fn(x) = 0, но 
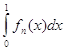= 1,
и этот интеграл не стремится к нулю.
Поэтому естественно поставить вопрос о тех дополнительных ограничениях, которые нужно наложить на функцию fn(x), чтобы равенство (1) все же имело место.
Мы ограничимся доказательством следующей теоремы.
Теорема (А. Лебег). Пусть на измеримом множестве Е задана последовательность f1(x), f2(x), f3(x), ¼ измеримых ограниченных функций, сходящаяся по мере к измеримой ограниченной функции F(х)
fn(x) Þ F(x).
Если существует постоянная К, такая, что при всех п и лри всех х
< K,
то
= (1)
Доказательство. Прежде всего заметим, что почти для всех х Î Е будет
£ K. (2)
В самом деле, из последовательности {fn(x)} можно (на основании теоремы Рисса) извлечь частичную последовательность {
(x)}, которая сходится к F(x) почти везде. Во всех точках, где
(x) ® F(x),
можно перейти к пределу в неравенстве 
< K, что и приводит к (2).
Пусть теперь s есть положительное число. Положим,
An(s) = E(
)³s), Bn(s) = E()<s.
Тогда
£ 
= 
+ 
.
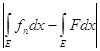В силу неравенства 
£ + , почтидля всех х из множества An(s) будет
< 2K,
так что по теореме о среднем
£ 2K× mAn(s)
(3)
(то обстоятельство, что неравенство < 2К может не выполняться на множестве меры 0, несущественно. Можно, например, функцию на этом множестве изменить, сделав ее равной нулю; тогда неравенство (3) будет выполняться во всех точках А. Но так как изменение функции на множестве меры 0 не влияет на величину интеграла, то (3) верно и без такого изменения).
С другой стороны, опять-таки в силу теоремы о среднем,
£ smBn(s) £ smE.
Сопоставляя это с (3), находим, что
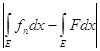£ 2K× mAn(s) + smE.
(4)
Заметив это, возьмем произвольное e > 0 и найдем столь малое s > 0, что
s× mE < 
.
Фиксировав это s, мы, на основании самого определения сходимости по мере, будем иметь, что при n ® ¥
mAn(s) ® 0
и, стало быть, для n > N окажется
2K× mAn(s) < .
Для этих n неравенство (4) примет вид
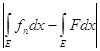< e,
что и доказывает теорему.
Легко понять, что теорема остается верной и в том случае, когда неравенство
< K
выполняется только почти везде на множестве Е. Доказательство остается прежним.
Далее, поскольку сходимость по мере общее обычной сходимости, то теорема и подавно сохраняет силу для того случая, когда
fn(x) ® F(x)
почти везде (и тем более везде).
Похожие работы
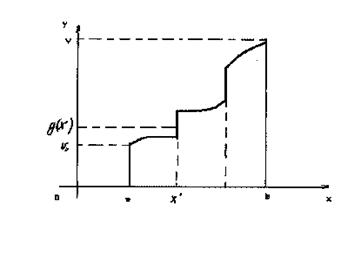
... 2.6 Приведение интеграла Стилтьеса к интегралу Римана Пусть функция непрерывна в промежутке , а монотонно возрастает в этом промежутке, и притом в строгом смысле. Тогда, как показал Лебег, интеграл Стилтьеса с помощью подстановки непосредственно приводится к интегралу Римана. На рисунке изображен график функции . Для тех значений , при которых функция испытывает скачок (ибо мы вовсе ...
... функции стремятся к нулю при . Если соотношение (7) имеет место для всякой суммируемой на [a, b] функции f (t), то мы будем говорить, что последовательность слабо сходится к нулю. §2. Представление функции сингулярным интегралом в заданной точке Во всем дальнейшем будем считать, что ядро при фиксированных n и x ограничено. Тогда сингулярный интеграл имеет смысл при любой ...
... и в том случае, когда интегральный оператор (3) действует в пространстве C(W) и неразложим в этом пространстве относительно конуса неотрицательных функций пространства C(W). Получению оценок спектрального радиуса положительного оператора по информации о поведении этого оператора на фиксированном ненулевом элементе конуса посвящена достаточно обширная литература [21], [11], [13], [18], [26], ...
... интегралы всех разрывных функций, которые можно было построить известными в то время методами (интеграл Лебега). Триумф идей Лебега привел к тому, что даже один из вождей математиков – классиков Гастон Дарбу изменил свое мнение и, выступая в 1908г. на Математическом конгрессе в Риме, говорил о пламенном и пытливом духе математики ХХ в., о науке, ведущей свои изыскания в абсолютно новой области с ...
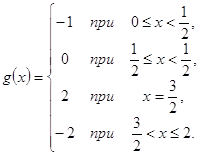
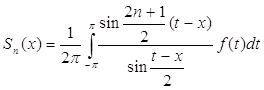
0 комментариев