Алгоритм Евклида

2.2.2. Алгоритм Евклида

Вычислим - остаток от деления числа на , , .

Если , то есть искомое число.

Если , то заменим пару чисел парой и перейдем к
шагу 1.

Теорема 1. При вычислении наибольшего общего делителя с помощью алгоритма Евклида будет выполнено не более операций де­ления с остатком, где есть количество цифр в десятичной записи меньшего из чисел и .

Доказательство. Положим и определим - последовательность делителей, появляющихся в процессе выполнения ша­га 1 алгоритма Евклида. Тогда

.

Пусть также , , , , - последователь­ность Фибоначчи. Индукцией по от до легко доказывается неравенство . А так как , то имеем неравенства и .

Немного подправив алгоритм Евклида, можно достаточно быстро ре­шать сравнения при условии, что . Эта задача равносильна поиску целых решений уравнения .

2.2.3. Алгоритм решения уравнения

0) Определим матрицу .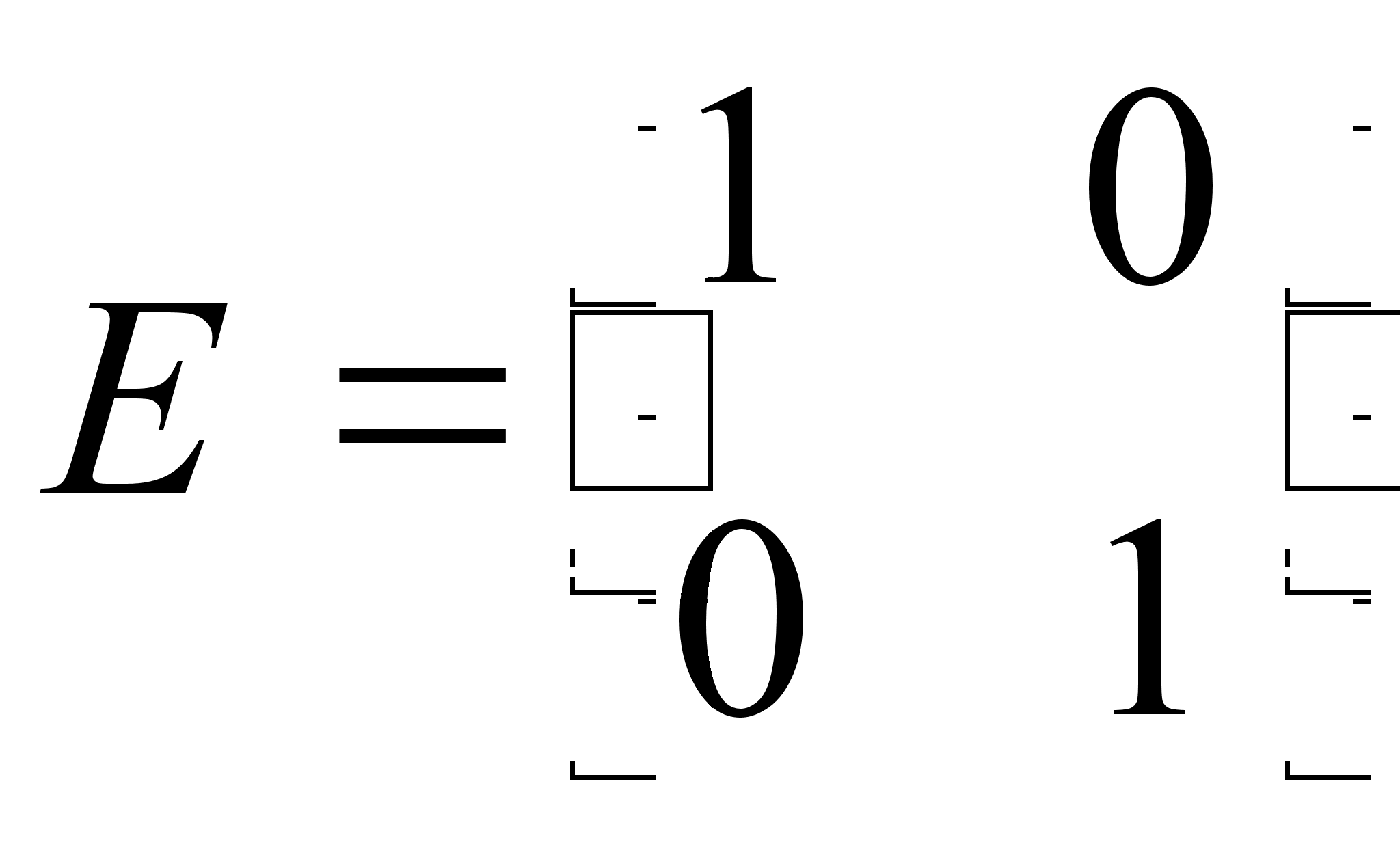

1) Вычислим - остаток от деления числа на , , .

Если , то второй столбец матрицы даёт вектор
решений уравнения.

Если , то заменим матрицу матрицей .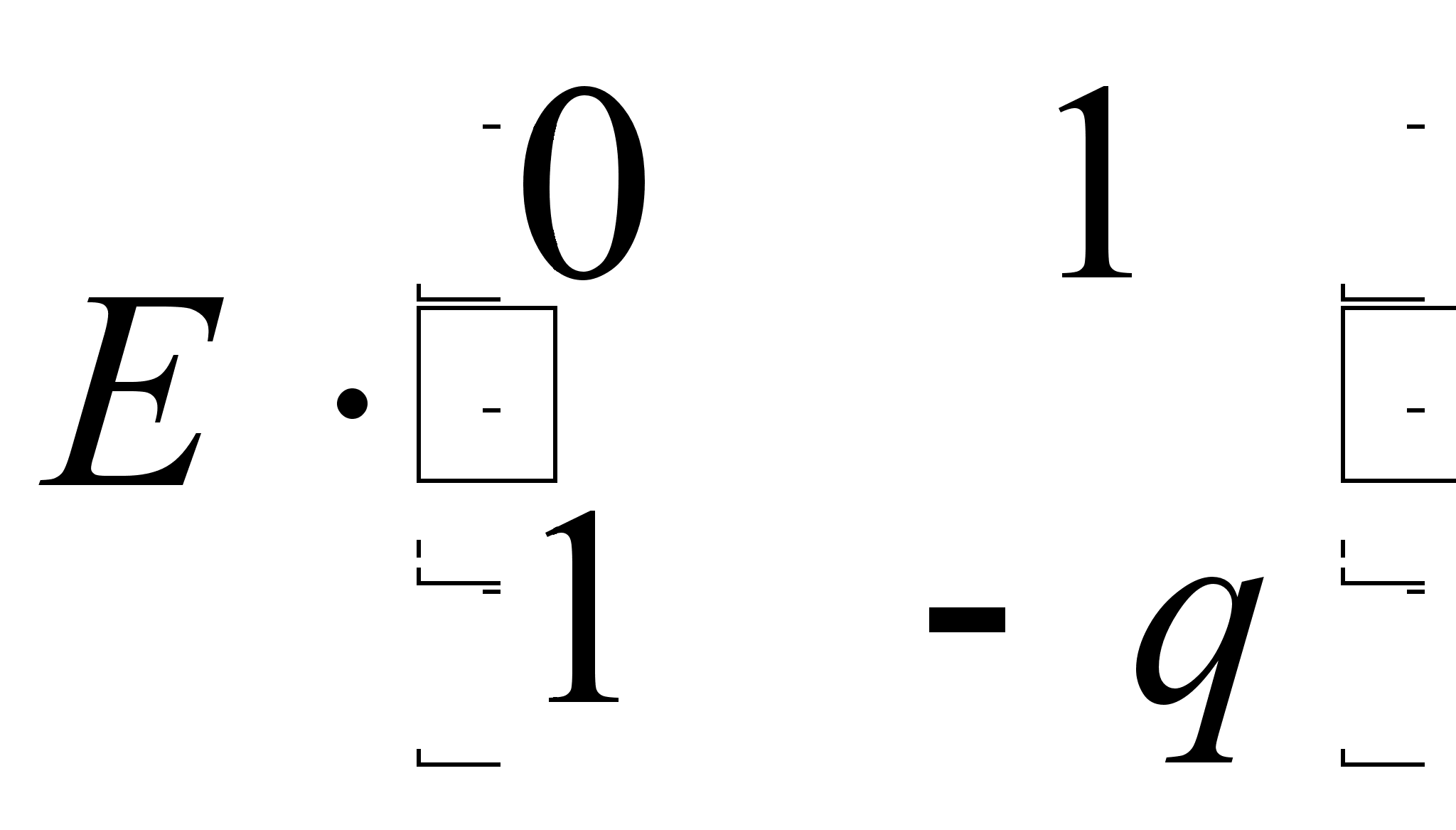

Заменим пару чисел парой и перейдем к шагу 1.

Если обозначить через матрицу , возникающую в процессе рабо­ты алгоритма перед шагом 2 после делений с остатком (шаг 1), то в обозначениях из доказательства теоремы 1 в этот момент выполняется векторное равенство . Поскольку числа и взаимно просты, имеем , и это доказы­вает, что алгоритм действительно даёт решение уравнения . Буквой мы обозначили количество делений с остатком, которое в точ­ности такое же, как и в алгоритме Евклида.

Три приведённых выше алгоритма относятся к разряду так называе­мых полиномиальных алгоритмов. Это название носят алгоритмы, слож­ность которых оценивается сверху степенным образом в зависимости от длины записи входящих чисел. Если наибольшее из чисел, подаваемых на вход алгоритма, не превосходит , то сложность алгоритмов этого типа оценивается величиной , где - некото­рая абсолютная постоянная. Во всех приведённых выше примерах .

Полиномиальные алгоритмы в теории чисел - большая редкость. Да и опенки сложности алгоритмов чаше всего опираются на какие-либо не доказанные, но правдоподобные гипотезы, обычно относящиеся к анали­тической теории чисел.

Для некоторых задач эффективные алгоритмы вообще не известны. Иногда в таких случаях все же можно предложить последовательность действий, которая, «если повезет», быстро приводит к требуемому ре­зультату. Существует класс так называемых вероятностных алгоритмов, которые дают правильный результат, но имеют вероятностную опен­ку времени работы. Обычно работа этих алгоритмов зависит от одного или нескольких параметров. В худшем случае они работают достаточно долго. Но удачный выбор параметра определяет быстрое завершение ра­боты. Такие алгоритмы, если множество «хороших» значений параметров велико, на практике работают достаточно эффективно, хотя и не имеют хороших опенок сложности.

Мы будем иногда использовать слова детерминированный алгоритм, чтобы отличать алгоритмы в обычном смысле от вероятностных алго­ритмов.

Как пример, рассмотрим вероятностный алгоритм, позволяющий эф­фективно находить решения полиномиальных сравнений по простому мо­дулю. Пусть — простое число, которое предполагается большим, и - многочлен, степень которого предполагается ограничен­ной. Задача состоит в отыскании решений сравнения

. (8)

Например, речь может идти о решении квадратичных сравнений, если степень многочлена равна 2. Другими словами, мы должны отыскать в поле все элементы, удовлетворяющие уравнению .

Согласно малой теореме Ферма, все элементы поля являются од­нократными корнями многочлена . Поэтому, вычислив наибольший общий делитель , мы найдем многочлен , множест­во корней которого в поле совпадает с множеством корней многочлена , причем все эти корни однократны. Если окажется, что многочлен имеет нулевую степень, т. е. лежит в поле , это будет означать, что сравнение (8) не имеет решений.

Для вычисления многочлена удобно сначала вычислить многочлен , пользуясь алгоритмом, подобным описанному выше алгоритму возведения в степень (напомним, что число предполагается большим). А затем с помощью аналога алгоритма Евклида вычислить . Всё это выполняется за полиномиальное количество арифметических операций.

Таким образом, обсуждая далее задачу нахождения решений сравне­ния (8), мы можем предполагать, что в кольце многочленов спра­ведливо равенство

2.2.4. Алгоритм нахождения делителей многочлена в коль­це

1) Выберем каким-либо способом элемент .

Вычислим наибольший общий делитель .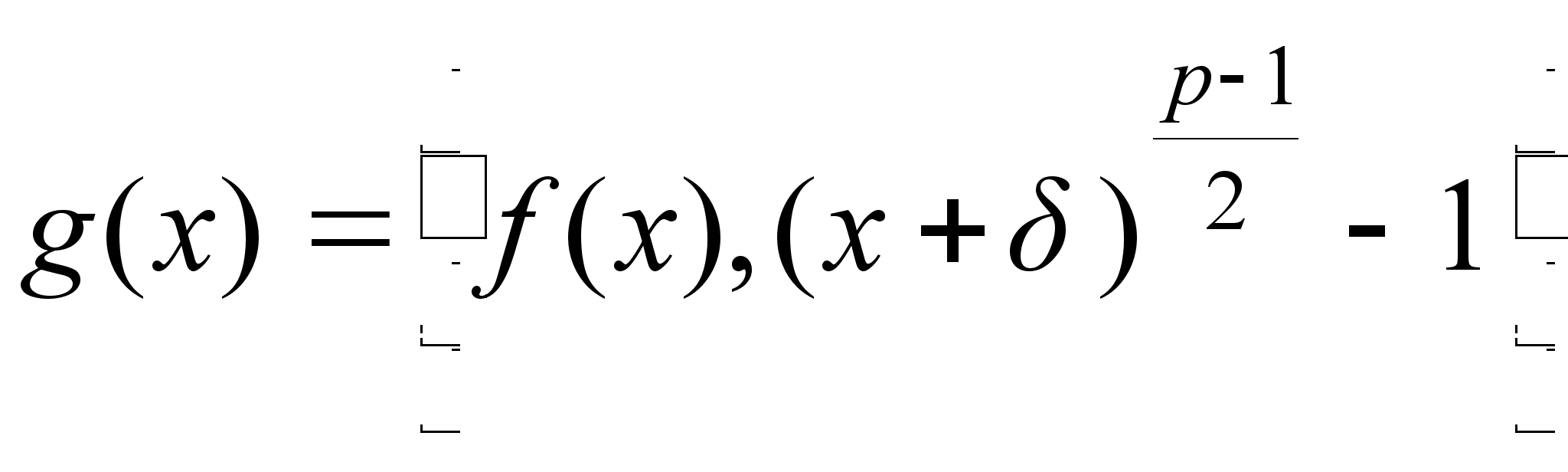

Если многочлен окажется собственным делителем , то многочлен распадётся на два множителя и с каждым из них незави­симо нужно будет проделать все операции, предписываемые настоящим алгоритмом для многочлена .

4) Если окажется, что или , следует перейти к шагу 1 и. выбрав новое значение , продолжить выполнение алгоритма.

Количество операций на шаге 2 оценивается величиной , ес­ли вычисления проводить так, как это указывалось выше при нахожде­нии . Выясним теперь, сколь долго придётся выбирать числа , пока на шаге 2 не будет найден собственный делитель .

Количество решений уравнения в поле не превосходит . Это означает, что подмножество элементов , удовлетворяющих условиям

,

состоит не менее, чем из элементов. Учитывая теперь, что каждый ненулевой элемент удовлетворяет одному из равенств , либо , заключаем, что для одно из чисел будет корнем многочлена , а другое - нет. Для таких элементов многочлен , определённый на шаге 2 алгоритма, будет собственным делителем многочлена .

Итак, существует не менее «удачных» выборов элемента , при которых на шаге 2 алгоритма многочлен распадётся на два соб­ственных множителя. Следовательно, при «случайном» выборе элемента , вероятность того, что многочлен не разложится на множители после повторений шагов алгоритма 1-4. не превосходит . Вероят­ность с ростом убывает очень быстро. И действительно, на практике этот алгоритм работает достаточно эффективно.

Заметим, что при опенке вероятности мы использовали только два корня многочлена . При эта вероятность, конечно, еще меньше. Более тонкий анализ с использованием опенок А. Вейля для сумм харак­теров показывает, что вероятность для многочлена не распасться на множители при однократном проходе шагов алгоритма 1-4. не пре­восходит . Здесь постоянная в зависит от .

Если в сравнении (8) заменить простой модуль составным моду­лем , то задача нахождения решений соответствующего сравнения ста­новится намного более сложной. Известные алгоритмы её решения осно­ваны на сведении сравнения к совокупности сравнений (8) по простым модулям — делителям , и. следовательно, они требуют разложения чи­сла то на простые сомножители, что, как уже указывалось, является до­статочно трудоемкой задачей.

Похожие работы

Шифросистемы с открытым ключом. Их возможности и применение.

Скачать

31031

1

0

... в тайне. Исходный текст шифруется открытым ключом адресата и передается ему. Зашифрованный текст в принципе не может быть расшифрован тем же открытым ключом. Дешифрование сообщение возможно только с использованием закрытого ключа, который известен только самому адресату. Криптографические системы с открытым ключом используют так называемые необратимые или ...

Защита персональных данных с помощью алгоритмов шифрования

Скачать

50231

14

1

... . Так как система с открытыми ключами позволяет распределять ключи и в симметричных системах, можно объединить в системе передачи защищенной информации асимметричный и симметричный алгоритмы шифрования. С помощью первого рассылать ключи, вторым же - собственно шифровать передаваемую информацию Обмен информацией можно осуществлять следующим образом: ·          получатель вычисляет открытый и ...

Устройство аппаратного шифрования данных с интерфейсом USB

Скачать

86939

6

20

... схема устройства для аппаратного шифрования информации, которая соответствует приведенным выше требованиям, изображена на рисунке 1.9. Рис. 1.9 – Структурная схема устройства аппаратного шифрования 2.  РАЗРАБОТКА СХЕМОТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ АППАРАТНОГО ШИФРАТОРА 2.1  Выбор элементной базы для шифратора   Согласно техническому заданию, элементная база для аппаратного шифратора должна ...

Криптографические системы защиты данных

Скачать

61238

6

2

... не к ключам!) и поэтому может зашифровывать и дешифровывать любую информацию; 2.7 Выводы по разделу 2. Подводя итоги вышесказанного, можно уверенно заявить, что криптографическими системами защиты называються совокупность различных методов и средств, благодаря которым исходная информация кодируеться, передаеться и расшифровываеться. Существуют различные криптографические системы защиты, ...