Проверка большого числа на простоту

3.3. Проверка большого числа на простоту

Есть некоторое отличие в постановках задач предыдущего и настоя­щего пунктов. Когда мы строим простое число , мы обладаем некото­рой дополнительной информацией о нем, возникающей в процессе постро­ения. Например, такой информацией является знание простых делителей числа . Эта информация иногда облегчает доказательство просто­ты .

В этом пункте мы предполагаем лишь, что нам задано некоторое чи­сло , например, выбранное случайным образом на каком-то промежут­ке, и требуется установить его простоту, или доказать, что оно является составным. Эту задачу за полиномиальное количество операций решает указанный в п. 3 алгоритм Миллера. Однако, справедливость полученного с его помощью утверждения зависит от недоказанной расширенной гипо­тезы Римана. Если число выдержало испытания алгоритмом 5 для 100 различных значений параметра , то, по-видимому, можно утверждать, что оно является простым с вероятностью большей, чем . Эта вероятность очень близка к единице, однако всё же оставляет некоторую тень сомнения на простоте числа . В дальнейшем в этом пункте мы будем считать, что заданное число является простым, а нам требуется лишь доказать это.

В настоящее время известны детерминированные алгоритмы различ­ной сложности для доказательства простоты чисел. Мы остановимся по­дробнее на одном из них, предложенном в 1983 г. в совместной работе Адлемана. Померанца и Рамели. Для доказательства простоты или непростоты числа этот алгоритм требует арифметиче­ских операций. Здесь - некоторая положительная абсолютная посто­янная. Функция хоть и медленно, но всё же возрастает с ростом , поэтому алгоритм не является полиномиальным. Но всё же его прак­тические реализации позволяют достаточно быстро тестировать числа на простоту. Существенные усовершенствования и упрощения в перво­начальный вариант алгоритма были внесены в работах X. Ленстры и А. Коена. Мы будем называть описываемый ниже алгоритм алго­ритмом Адлемана - Ленстры.

В основе алгоритма лежит использование сравнений типа малой те­оремы Ферма, но в кольцах целых чисел круговых полей, т. е. полей. порождённых над полем числами - корнями из 1. Пусть - простое нечётное число и — первообразный корень по модулю , т. е. образующий элемент мультипликативной группы поля , которая пиклична. Для каждого целого числа , не делящегося на , можно опре­делить его индекс, , называемый также дискретным логарифмом, с помощью сравнения . Рассмотрим далее два простых числа , с условием, что делится на , но не делится на .

Следующая функция, определённая на множестве целых чисел.

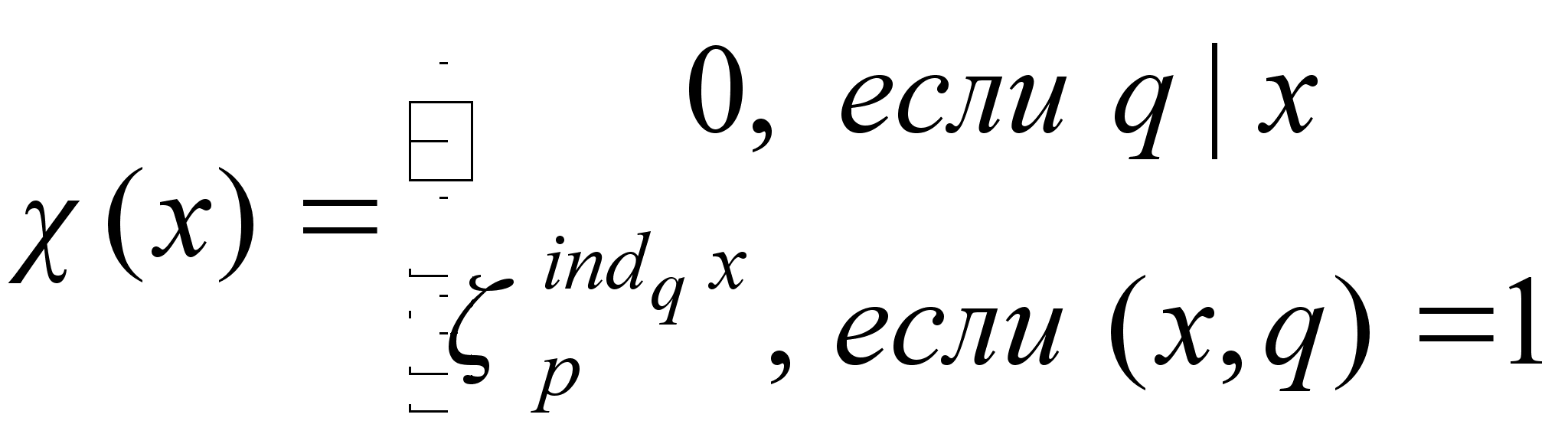
является характером по модулю и порядок этого характера равен .

Сумма

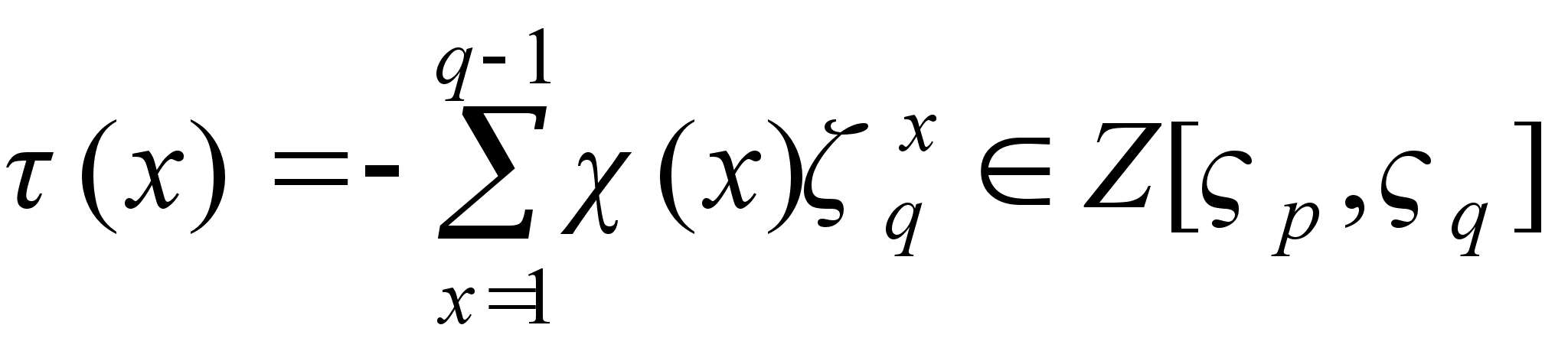
называется суммой Гаусса. Формулируемая ниже теорема 3 представляет собой аналог малой теоремы Ферма, используемый в алгоритме Адлемана - Ленстры.

Теорема 3. Пусть - нечетное простое число, . Тогда в кольце выполняется сравнение

.

Если при каких-либо числах сравнение из теоремы 3 нарушается. можно утверждать, что составное число. В противном случае, если сравнение выполняется, оно даёт некоторую информацию о возможных простых делителях числа . Собрав такую информацию для различных , в конце концов удаётся установить, что имеет лишь один простой делитель и является простым.

В случае легко проверить, что сравнение из теоремы 3 равно­сильно хорошо известному в элементарной теории чисел сравнению

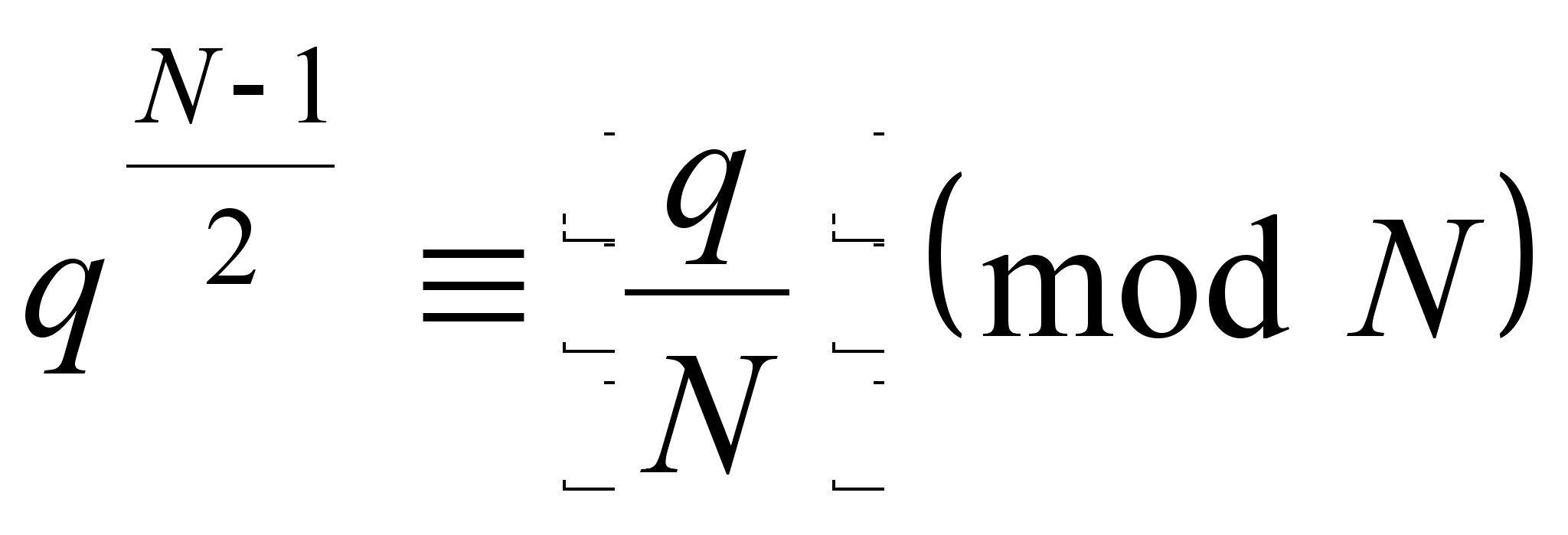, (13)

где - так называемый символ Якоби. Хорошо известно также, что последнее сравнение выполняется не только для простых , но и для любых целых , взаимно простых с . Заметим также, что для вычисления символа Якоби существует быстрый алгоритм, основанный на законе вза­имности Гаусса и. в некотором смысле, подобный алгоритму Евклида вы­числения наибольшего общего делителя. Следующий пример показывает. каким образом выполнимость нескольких сравнений типа (13) даёт неко­торую информацию о возможных простых делителях числа .

Пример (X. Ленстра). Пусть — натуральное число, . для которого выполнены сравнения

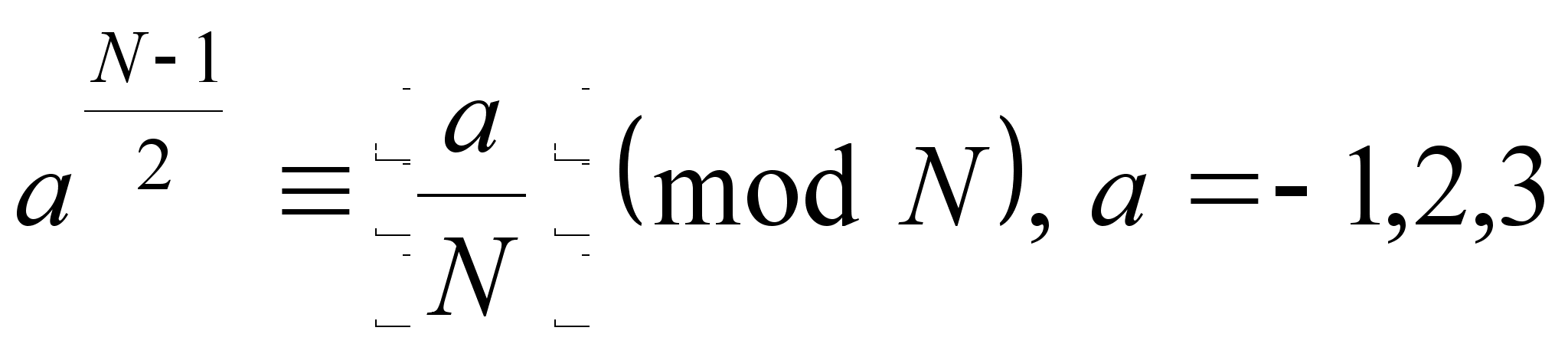, (14)

а кроме того с некоторым целым числом имеем

. (15)

Как уже указывалось, при простом сравнения (14) выполняются для любого , взаимно простого с , а сравнение (15) означает, что есть первообразный корень по модулю . Количество первообразных корней равно , т. е. достаточно велико. Таким образом, число с усло­вием (15) при простом может быть найдено достаточно быстро с помощью случайного выбора и последующей проверки (15).

Докажем, что из выполнимости (14-15) следует, что каждый делитель числа удовлетворяет одному из сравнений

или . (16)

Не уменьшая общности, можно считать, что - простое число. Введем теперь обозначения , где и - нечётные числа. Из (15) и сравнения следует, что . Далее, согласно (14). выполняются следующие сравнения

,

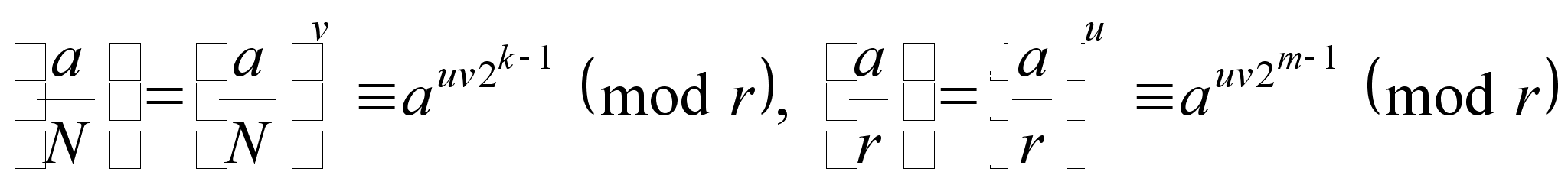означающие (в силу того, что символ Якоби может равняться лишь -1 или +1), что

.

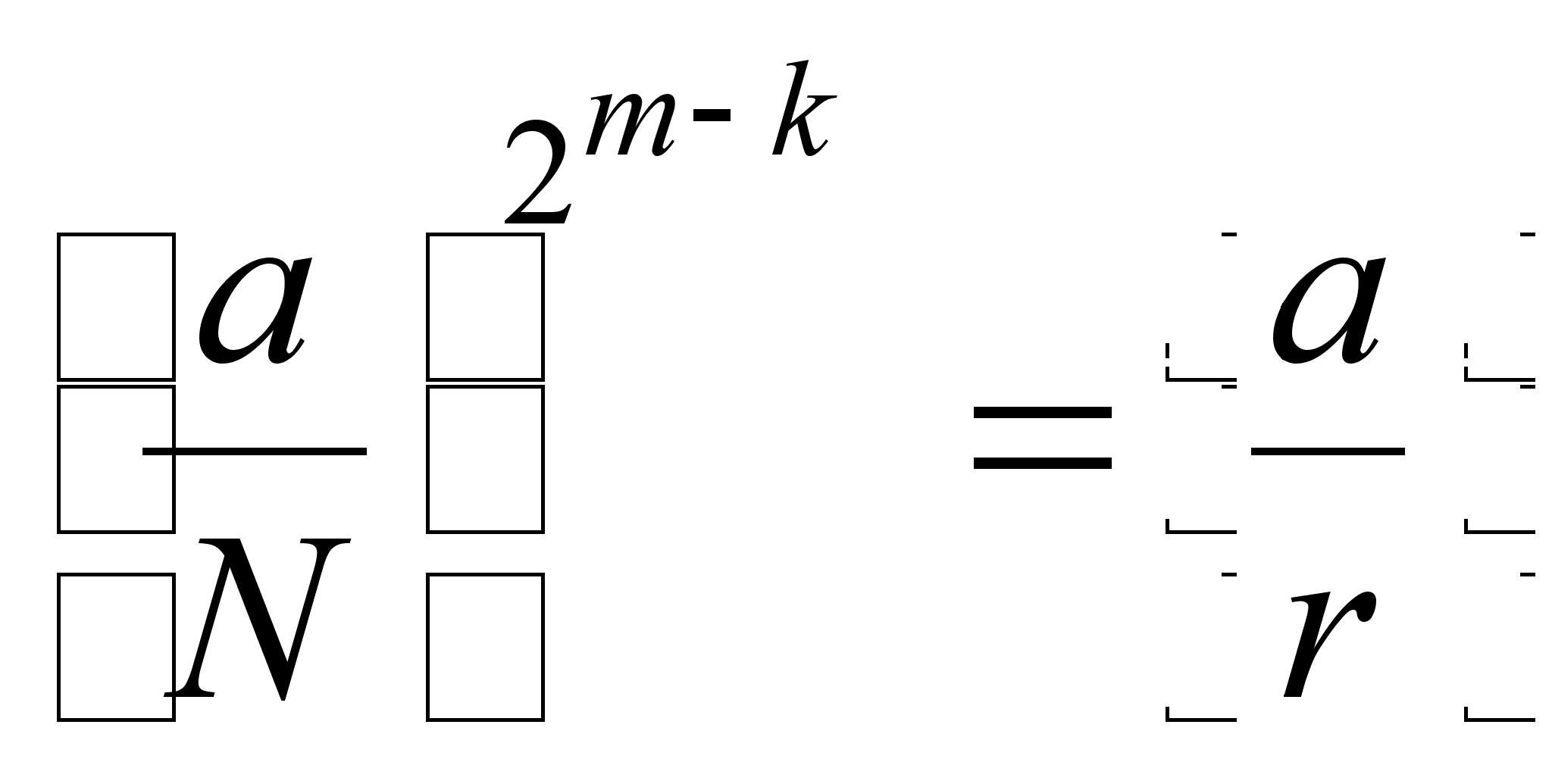При это равенство означает, что 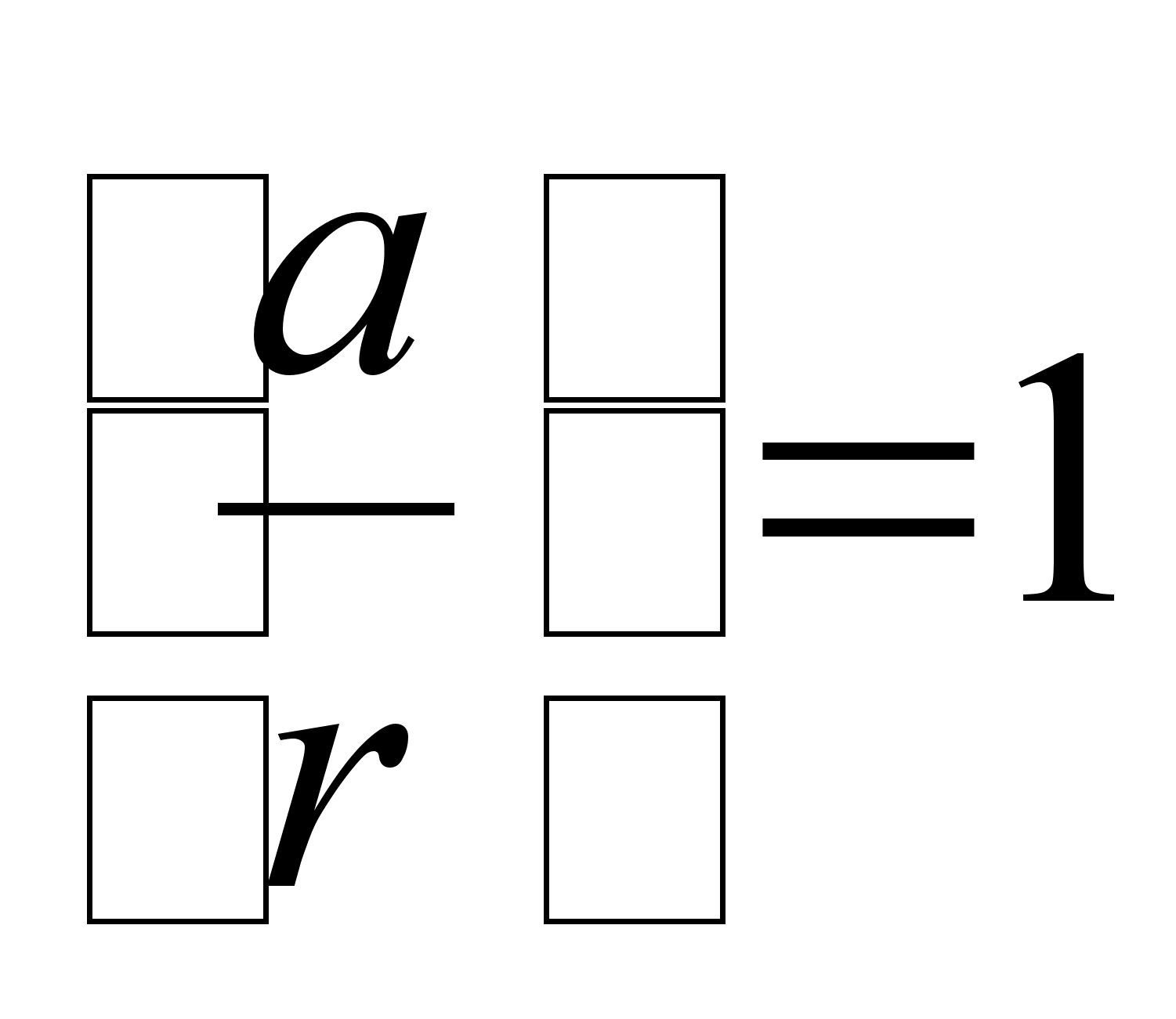при , и, следовательно, . Если же , то имеем 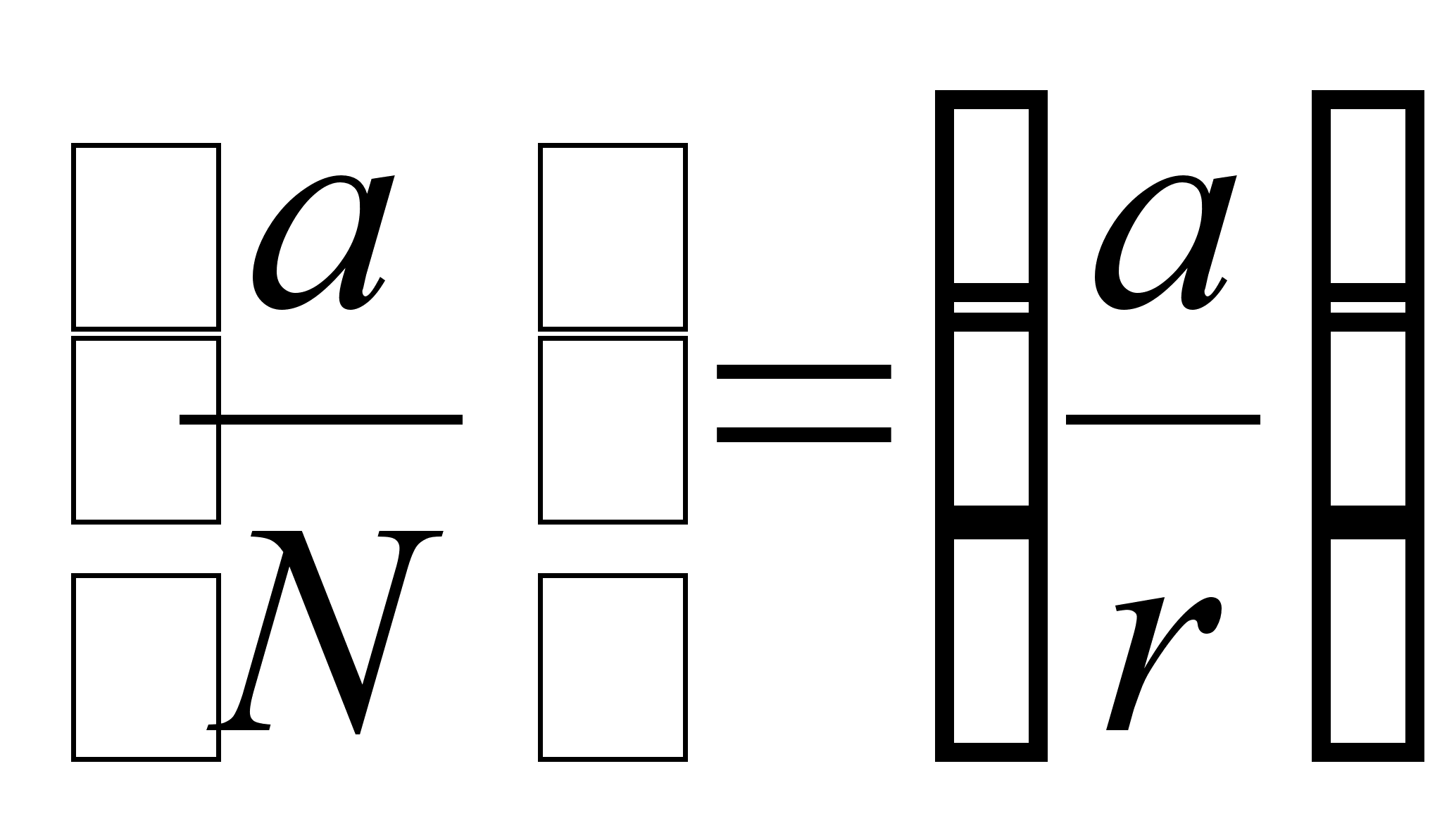и . Этим (16) доказано.

Информация такого рода получается и в случае произвольных про­стых чисел и с указанными выше свойствами.

Опишем схему алгоритма Адлемана - Ленстры для про­верки простоты :

1) выбираются различные простые числа и различные про­стые нечётные такие, что

1) для каждого все простые делители числа содержатся
среди и не делятся на квадрат простого числа;

1) .

для каждой пары выбранных чисел , проводятся тесты, подобные сравнению из теоремы 3. Если не удовлетворяет какому-либо из
этих тестов - оно составное. В противном случае

определяется не очень большое множество чисел, с которыми толь­ко и могут быть сравнимы простые делители . А именно, каждый простой делитель числа должен удовлетворять сравнению вида

, .

4) проверяется, содержит ли найденное множество делители . Ес­ли при этом делители не обнаружены, утверждается, что - простое
число.

Если число составное, оно обязательно имеет простой делитель , меньший , который сам содержится среди возможных остатков. Именно на этом свойстве основано применение пункта 4) алгоритма.

Сумма Якоби

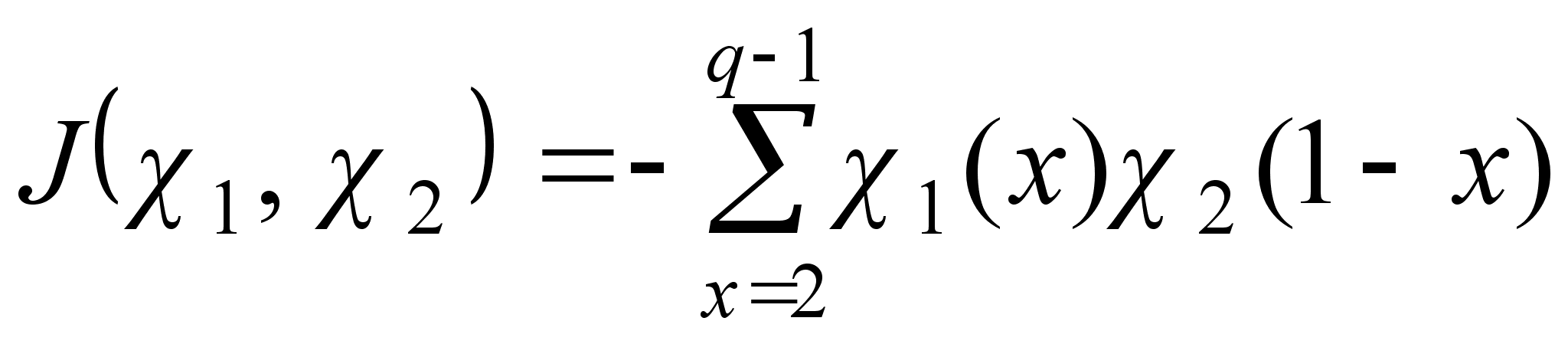
определяется для двух характеров модулю . Если характеры имеют порядок , то соответствующая сумма Якоби принадлежит кольцу . Поскольку числа , участвующие в алгоритме, сравнительно невели­ки, то вычисления с суммами Якоби производятся в полях существенно меньшей степени, чем вычисления с суммами Гаусса. Это главная при­чина, по которой суммы Якоби предпочтительнее для вычислений. При выполняется классическое соотношение

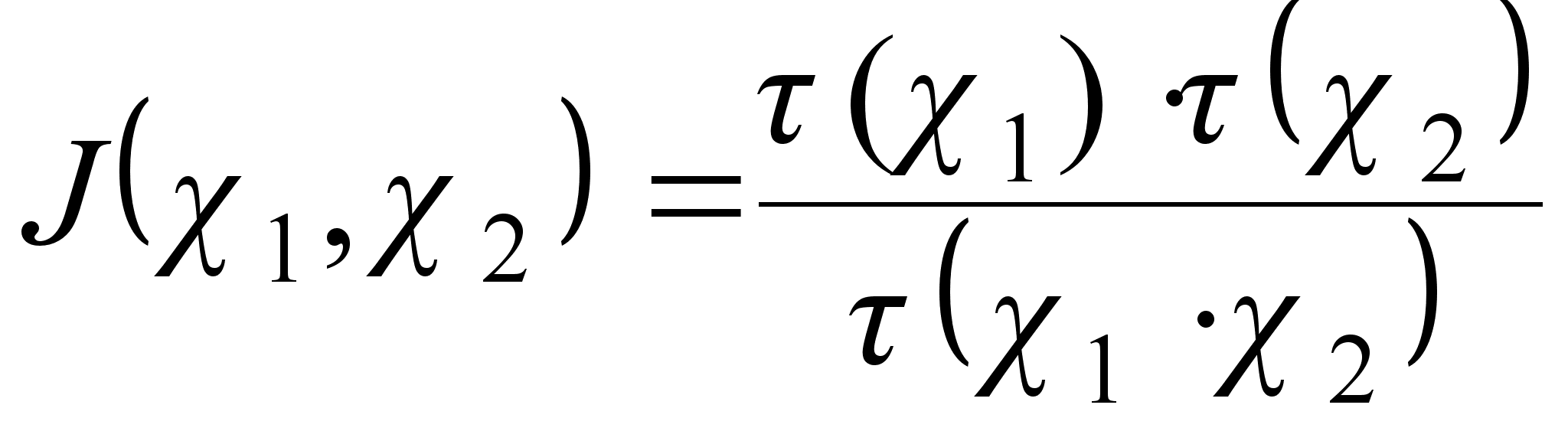
связывающее суммы Гаусса с суммами Якоби и позволяющее переписать сравнение теоремы 3 в терминах сумм Якоби. Так. при и соответствующее сравнение, справедливое для простых , отлич­ных от 2,3,7, принимает вид

,

где и - некоторый корень кубический из 1.

В 1984 г. было внесено существенное усовершенствование в алгоритм, позволившее освободиться от требования неделимости чисел на квадраты простых чисел. В результате, например, выбрав число и взяв равным произведению простых чисел с условием, что делится на , получим , что позволяет доказывать простоту чисел , записываемых сотней десятичных знаков. При этом вычисления будут проводиться в полях, порождённых корнями из 1 степеней 16, 9, 5 и 7.

Персональный компьютер с процессором Pentium-150. пользуясь реализацией этого алгоритма на языке UBASIC, доказал простоту записываемого 65 десятичными знаками, большего из простых чисел в при­мере Ривеста, Шамира и Адлемана за 8 секунд. Сравнение этих 8 секунд и 17 лет, потребовавшихся для разложения на множители предложенного в примере числа, конечно, впечатляет.

Отметим, что опенка сложности этого алгоритма представляет со­бой трудную задачу аналитической теории чисел. Как уже указывалось, количество операций оценивается величиной . Однако соот­ветствующие числа и , возникающие в процессе доказательства, не могут быть явно указаны в зависимости от . Доказано лишь существо­вание чисел и , для которых достигается оценка. Впрочем, есть веро­ятностный вариант алгоритма, доказывающий простоту простого числа с вероятностью большей за арифметических операций. А в предположении расширенной гипотезы Римана эта опенка сложности может быть получена при эффективно указанных и.

Похожие работы

Шифросистемы с открытым ключом. Их возможности и применение.

Скачать

31031

1

0

... в тайне. Исходный текст шифруется открытым ключом адресата и передается ему. Зашифрованный текст в принципе не может быть расшифрован тем же открытым ключом. Дешифрование сообщение возможно только с использованием закрытого ключа, который известен только самому адресату. Криптографические системы с открытым ключом используют так называемые необратимые или ...

Защита персональных данных с помощью алгоритмов шифрования

Скачать

50231

14

1

... . Так как система с открытыми ключами позволяет распределять ключи и в симметричных системах, можно объединить в системе передачи защищенной информации асимметричный и симметричный алгоритмы шифрования. С помощью первого рассылать ключи, вторым же - собственно шифровать передаваемую информацию Обмен информацией можно осуществлять следующим образом: ·          получатель вычисляет открытый и ...

Устройство аппаратного шифрования данных с интерфейсом USB

Скачать

86939

6

20

... схема устройства для аппаратного шифрования информации, которая соответствует приведенным выше требованиям, изображена на рисунке 1.9. Рис. 1.9 – Структурная схема устройства аппаратного шифрования 2.  РАЗРАБОТКА СХЕМОТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ АППАРАТНОГО ШИФРАТОРА 2.1  Выбор элементной базы для шифратора   Согласно техническому заданию, элементная база для аппаратного шифратора должна ...

Криптографические системы защиты данных

Скачать

61238

6

2

... не к ключам!) и поэтому может зашифровывать и дешифровывать любую информацию; 2.7 Выводы по разделу 2. Подводя итоги вышесказанного, можно уверенно заявить, что криптографическими системами защиты называються совокупность различных методов и средств, благодаря которым исходная информация кодируеться, передаеться и расшифровываеться. Существуют различные криптографические системы защиты, ...