Нахождение больших простых чисел

3.2. Нахождение больших простых чисел

Конечно же, большие простые числа можно строить сравнительно быстро. При этом можно обеспечить их случайное распределение в заданном диапазоне величин. В противном случае теряла бы всякий практический смысл система шифрования RSA. Наиболее эффективным средством построения простых чисел является несколько модифицированная малая теорема Ферма.

Теорема 2. Пусть - нечётные натуральные числа, , причем для каждого простого делителя числа существует целое число такое, что

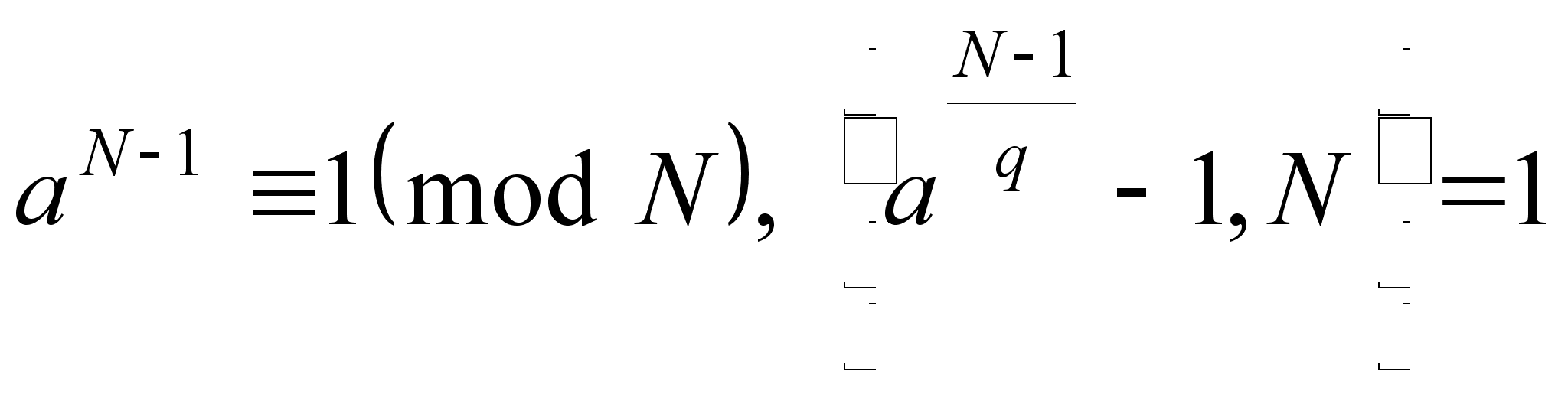. (10)

Тогда каждый простой делитель числа удовлетворяет сравнению

.

Доказательство. Пусть - простой делитель числа , a - не­который делитель . Из условий (10) следует, что в поле вычетов спра­ведливы соотношения

. (11)

Обозначим буквой порядок элемента в мультипликативной группе поля . Первые два из соотношений (11) означают, что входит в раз­ложение на простые множители числа в степени такой же, как и в раз­ложение , а последнее - что делится на . Таким образом, каждый простой делитель числа входит в разложение в степени не меньшей, чем в , так что делится на . Кроме того, четно. Теорема 2 доказана.

Следствие. Если выполнены условия теоремы 2 и , то - простое число.

Действительно, пусть равняется произведению не менее двух про­стых чисел. Каждое из них, согласно утверждению теоремы 2, не меньше, чем . Но тогда . Противоречие и доказывает следствие.

Покажем теперь, как с помощью последнего утверждения, имея боль­шое простое число , можно построить существенно большее простое число . Выберем для этого случайным образом чётное число на про­межутке и положим . Затем проверим число на отсутствие малых простых делителей, разделив его на малые простые числа; испытаем некоторое количество раз с помощью алгоритма 5. Если при этом выяснится, что - составное число, следует выбрать новое значение и опять повторить вычисления. Так следует делать до тех пор, пока не будет найдено число , выдержавшее испытания алго­ритмом 5 достаточно много раз. В этом случае появляется надежда на то, что - простое число, и следует попытаться доказать простоту с помощью тестов теоремы 2.

Для этого можно случайным образом выбирать число , и проверять для него выполнимость соотношений

. (12)

Если при выбранном эти соотношения выполняются, то, согласно след­ствию из теоремы 2, можно утверждать, что число простое. Если же эти условия нарушаются, нужно выбрать другое значение и повторять эти операции до тех пор, пока такое число не будет обнаружено.

Предположим, что построенное число действительно является про­стым. Зададимся вопросом, сколь долго придётся перебирать числа , по­ка не будет найдено такое, для которого будут выполнены условия (12). Заметим, что для простого числа первое условие (12), согласно малой теореме Ферма, будет выполняться всегда. Те же числа , для которых на­рушается второе условие (12), удовлетворяют сравнению . Как известно, уравнение в поле вычетов имеет не более решений. Одно из них . Поэтому на промежутке имеется не более чисел, для которых не выполняются условия (12). Это означа­ет, что, выбирая случайным образом числа на промежутке , при простом можно с вероятностью большей, чем , найти чи­сло , для которого будут выполнены условия теоремы 2, и тем доказать, что действительно является простым числом.

Заметим, что построенное таким способом простое число будет удовлетворять неравенству , т. е. будет записываться вдвое боль­шим количеством цифр, чем исходное простое число . Заменив теперь число на найденное простое число и повторив с этим новым все указанные выше действия, можно построить еще большее простое число. Начав с какого-нибудь простого числа, скажем, записанного 10 десятич­ными цифрами (простоту его можно проверить, например, делением на маленькие табличные простые числа), и повторив указанную процедуру достаточное число раз. можно построить простые числа нужной величи­ны.

Обсудим теперь некоторые теоретические вопросы, возникающие в связи с нахождением числа , удовлетворяющего неравенствам , и такого, что - простое число. Прежде всего, со­гласно теореме Дирихле, доказанной еще в 1839 г., прогрессия , содержит бесконечное количество простых чисел. Нас интересуют простые числа, лежащие недалеко от начала прогрессии. Опенка наименьшего простого числа в арифметической прогрессии была полу­чена в 1944 г. Ю. В. Линником. Соответствующая теорема утверждает, что наименьшее простое число в арифметической прогрессии не превосходит , где - некоторая достаточно большая абсолютная постоянная.

Таким образом, в настоящее время никаких теоретических гарантий для существования простого числа не сущес­твует. Тем не менее опыт вычислений на ЭВМ показывает, что простые числа в арифметической прогрессии встречаются достаточно близко к её началу. Упомянем в этой связи гипотезу о существовании бесконечного количества простых чисел с условием, что число также простое, т. е. простым является уже первый член прогрессии.

Очень важен в связи с описываемым методом построения простых чисел также вопрос о расстоянии между соседними простыми числами в арифметической прогрессии. Ведь убедившись, что при некотором число составное, можно следующее значение взять равным и действовать так далее, пока не будет найдено простое число . И если расстояние между соседними простыми числами в прогрессии ве­лико, нет надежды быстро построить нужное число . Перебор чисел до того момента, как мы наткнемся на простое число окажется слишком долгим. В более простом вопросе о расстоянии между соседни­ми простыми числами и в натуральном ряде доказано лишь, что 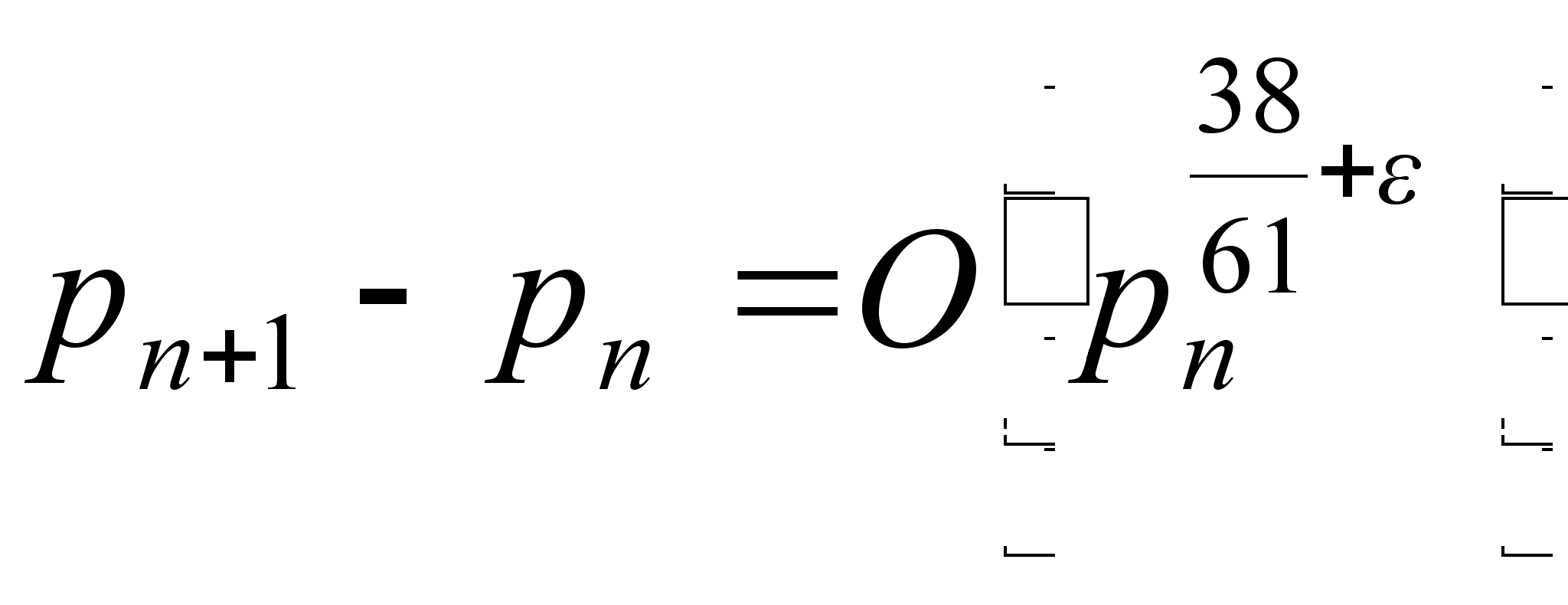, что, конечно, не очень хорошо для наших целей. Вместе с тем существует так называемая гипотеза Крамера (1936 г.), что , дающая вполне приемлемую опенку. Примерно такой же результат следует и из расширенной гипотезы Римана. Вычисления на ЭВМ показывают, что простые числа в арифметических прогрессиях расположены достаточно плотно.

В качестве итога обсуждения в этом пункте подчеркнём следующее: если принять на веру, что наименьшее простое число, а также расстояние между соседними простыми числами в прогрессии при оцениваются величиной , то описанная схема построения больших простых чисел имеет полиномиальную опенку сложности. Кро­ме того, несмотря на отсутствие теоретических опенок времени работы алгоритмов, отыскивающих простые числа в арифметических прогрес­сиях со сравнительно большой разностью, на практике эти алгоритмы работают вполне удовлетворительно. На обычном персональном компью­тере без особых затрат времени строятся таким способом простые числа порядка .

Конечно, способ конструирования простых чисел для использования в схеме RSA должен быть массовым, а сами простые числа должны быть в каком-то смысле хорошо распределёнными. Это вносит ряд дополнитель­ных осложнений в работу алгоритмов.

Наконец, отметим, что существуют методы построения больших про­стых чисел, использующие не только простые делители , но и делите­ли чисел . В основе их лежит использование после­довательностей целых чисел, удовлетворяющих линейным рекуррентным уравнениям различных порядков. Отметим, что последовательность , члены которой присутствуют в формулировке малой теоремы Ферма, со­ставляет решение рекуррентного уравнения первого порядка .

Похожие работы

Шифросистемы с открытым ключом. Их возможности и применение.

Скачать

31031

1

0

... в тайне. Исходный текст шифруется открытым ключом адресата и передается ему. Зашифрованный текст в принципе не может быть расшифрован тем же открытым ключом. Дешифрование сообщение возможно только с использованием закрытого ключа, который известен только самому адресату. Криптографические системы с открытым ключом используют так называемые необратимые или ...

Защита персональных данных с помощью алгоритмов шифрования

Скачать

50231

14

1

... . Так как система с открытыми ключами позволяет распределять ключи и в симметричных системах, можно объединить в системе передачи защищенной информации асимметричный и симметричный алгоритмы шифрования. С помощью первого рассылать ключи, вторым же - собственно шифровать передаваемую информацию Обмен информацией можно осуществлять следующим образом: ·          получатель вычисляет открытый и ...

Устройство аппаратного шифрования данных с интерфейсом USB

Скачать

86939

6

20

... схема устройства для аппаратного шифрования информации, которая соответствует приведенным выше требованиям, изображена на рисунке 1.9. Рис. 1.9 – Структурная схема устройства аппаратного шифрования 2.  РАЗРАБОТКА СХЕМОТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ АППАРАТНОГО ШИФРАТОРА 2.1  Выбор элементной базы для шифратора   Согласно техническому заданию, элементная база для аппаратного шифратора должна ...

Криптографические системы защиты данных

Скачать

61238

6

2

... не к ключам!) и поэтому может зашифровывать и дешифровывать любую информацию; 2.7 Выводы по разделу 2. Подводя итоги вышесказанного, можно уверенно заявить, что криптографическими системами защиты называються совокупность различных методов и средств, благодаря которым исходная информация кодируеться, передаеться и расшифровываеться. Существуют различные криптографические системы защиты, ...