КАЧЕСТВЕННАЯ ТЕОРИЯ АЛГОРИТМА RSA

3. КАЧЕСТВЕННАЯ ТЕОРИЯ АЛГОРИТМА RSA

Существует довольно эффективный способ убедиться, что заданное число является составным, не разлагая это число на множители. Согласно малой теореме Ферма, если число простое, то для любого целого , не делящегося на , выполняется сравнение

. (9)

Если же при каком-то это сравнение нарушается, можно утверждать, что - составное. Проверка (9) не требует больших вычислений, это следует из алгоритма 1. Вопрос только в том, как найти для составного целое число , не удовлетворяющее (9). Можно, например, пытаться найти необходимое число , испытывая все целые числа подряд, начиная с 2. Или попробовать выбирать эти числа случайным образом на отрезке .

К сожалению, такой подход не всегда даёт то, что хотелось бы. Име­ются составные числа , обладающие свойством (9) для любого целого с условием . Такие числа называются числами Кармайкла. Рассмотрим, например, число . Так как 560 делится на каждое из чисел 2, 10, 16, то с помощью малой теоремы Ферма легко проверить, что 561 есть число Кармайкла. Можно доказать, что любое из чисел Кармайкла имеет вид , где все простые различны, причем делится на каждую разность . Лишь недавно, была решена проблема о бесконечности множества таких чисел.

В 1976 г. Миллер предложил заменить проверку (9) проверкой несколь­ко иного условия. Если - простое число, , где нечётно, то согласно ма­лой теореме Ферма для каждого с условием хотя бы одна из скобок в произведении

делится на . Обращение этого свойства можно использовать, чтобы от­личать составные числа от простых.

Пусть - нечётное составное число, , где нечётно. Назовем целое число , , «хорошим» для , если нарушается одно из двух условий:

1) не делится на ;

2) или существует целое , , такое, что

.

Из сказанного ранее следует, что для простого числа не существует хороших чисел . Если же составное число, то, как доказал Рабин, их существует не менее .

Теперь можно построить вероятностный алгоритм, отличающий со­ставные числа от простых.

Похожие работы

Шифросистемы с открытым ключом. Их возможности и применение.

Скачать

31031

1

0

... в тайне. Исходный текст шифруется открытым ключом адресата и передается ему. Зашифрованный текст в принципе не может быть расшифрован тем же открытым ключом. Дешифрование сообщение возможно только с использованием закрытого ключа, который известен только самому адресату. Криптографические системы с открытым ключом используют так называемые необратимые или ...

Защита персональных данных с помощью алгоритмов шифрования

Скачать

50231

14

1

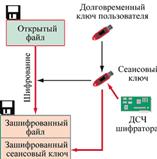
... . Так как система с открытыми ключами позволяет распределять ключи и в симметричных системах, можно объединить в системе передачи защищенной информации асимметричный и симметричный алгоритмы шифрования. С помощью первого рассылать ключи, вторым же - собственно шифровать передаваемую информацию Обмен информацией можно осуществлять следующим образом: ·          получатель вычисляет открытый и ...

Устройство аппаратного шифрования данных с интерфейсом USB

Скачать

86939

6

20

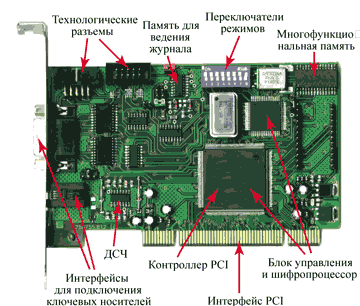
... схема устройства для аппаратного шифрования информации, которая соответствует приведенным выше требованиям, изображена на рисунке 1.9. Рис. 1.9 – Структурная схема устройства аппаратного шифрования 2.  РАЗРАБОТКА СХЕМОТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ АППАРАТНОГО ШИФРАТОРА 2.1  Выбор элементной базы для шифратора   Согласно техническому заданию, элементная база для аппаратного шифратора должна ...

Криптографические системы защиты данных

Скачать

61238

6

2

... не к ключам!) и поэтому может зашифровывать и дешифровывать любую информацию; 2.7 Выводы по разделу 2. Подводя итоги вышесказанного, можно уверенно заявить, что криптографическими системами защиты называються совокупность различных методов и средств, благодаря которым исходная информация кодируеться, передаеться и расшифровываеться. Существуют различные криптографические системы защиты, ...