Навигация
ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ
1. ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ
Вариант 80.
В цехе имеется токарный станок и станок-автомат. Цех выпускает детали 1,2 и 3 в комплекте: на каждую деталь 1 – по 2 детали 2 и 3. Часовая производительность станков по каждой из деталей приведена в таблице:
| Станки | Детали | ||
| 1 | 2 | 3 | |
| 1.Токарный | 5 | 5 | 10 |
| 2.Автомат | 15 | 15 | 10 |
Таблица 1. Часовая производительность станков
Составить программу работы станков, при которой в течение смены (8 часов) будет выпускаться максимальное количество комплектов деталей.
2. ПОСТРОЕНИЕ АНАЛИТИЧЕСКОЙ МОДЕЛИ
Составим аналитическую модель задачи. Для этого сначала введем переменные, которые требуется определить:
X1 – время, которое работал токарный станок над деталями типа 1 в течение рабочей смены;
X2 – время, которое работал токарный станок над деталями типа 2 в течение рабочей смены;
X3 – время, которое работал токарный станок над деталями типа 3 в течение рабочей смены;
X4 – время, которое работал станок-автомат над деталями типа 1 в течение рабочей смены;
X5 – время, которое работал станок-автомат над деталями типа 2 в течение рабочей смены;
X6 – время, которое работал станок-автомат над деталями типа 3 в течение рабочей смены.
Система ограничений состоит из двух групп. Первая группа устанавливает, что каждый из станков может работать не более 8 часов в смену.
Ограничение времени работы токарного станка:
X1 + X2 + X3 £ 8;
Ограничение времени работы станка-автомата:
X4 + X5 + X6 £ 8.
Вторая группа ограничений направлена на выполнение требования о комплектации деталей: на каждую деталь 1 должно приходиться по 2 детали 2 и 3. Но перед тем, как вводить это ограничение, определим, сколько деталей каждого типа у нас будет производиться за смену:
5X1 + 15X4 - будет произведено за смену деталей типа 1;
5X2 + 15X5 - будет произведено за смену деталей типа 2;
10X3 + 10X6 - будет произведено за смену деталей типа 3.
Теперь введем сами ограничения:
2(5X1 + 15X4) = 5X2 + 15X5;
2(5X1 + 15X4) = 10X3 + 10X6.
Очевидно, что все переменные в задаче неотрицательные (объем продукции не может быть отрицательным):
X1 , X2 , X3 , X4 , X5 , X6 ≥ 0.
Целевая функция в нашей задаче должна выражать количество комплектов деталей, выпускаемых за смену, поэтому сложим все выпускаемые детали и поделим на 5 (в комплект, как уже упоминалось, входят 1 деталь типа 1 и по 2 детали типа 2 и 3):
E= (5X1 + 15X4 + 5X2 + 15X5 + 10X3 + 10X6)/5 Þ max
или, если упростить это выражение, то получим:
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þ max
Целевую функцию надо максимизировать.
Таким образом, формальная постановка задачи оптимизации имеет следующий вид:
X1 + X2 + X3 £ 8;
X4 + X5 + X6 £ 8;
2(5X1 + 15X4) = 5X2 + 15X5;
2(5X1 + 15X4) = 10X1 + 10X6;
X1 , X2 , X3 , X4 , X5 , X6 ≥ 0.
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þ max
3. ОБОСНОВАНИЕ И ОПИСАНИЕ ВЫЧИСЛИТЕЛЬНОЙ ПРОЦЕДУРЫ3.1. ПРИВЕДЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ К СТАНДАРТНОЙ ФОРМЕ
Любая задача линейного программирования приводится к стандартной (канонической) форме основной задачи линейного программирования, которая формулируется следующим образом: найти неотрицательные значения переменных X1 , X2 , Xn , удовлетворяющих ограничениям в виде равенств:
A11X1 + A12X2 + … + A1nXn = B1;
A21X1 + A22X2 + … + A2nXn = B2;
……………………………………
Am1X1 + Am2X2 + … + AmnXn = Bm;
Xj ≥ 0, j=1,…,n
и обращающих в максимум линейную функцию этих переменных:
E = C1X1 + C2X2 + … + CnXn Þ max
При этом также требуется, чтобы правые части равенств были неотрицательны, т.е. должны соблюдаться условия:
Bj ≥ 0, j=1,…,n
Приведение к стандартной форме необходимо, так как большинство методов решения задач линейного программирования разработано именно для стандартной формы. Для приведения к стандартной форме задачи линейного программирования может потребоваться выполнить следующие действия:
- перейти от минимизации целевой функции к ее максимизации;
- изменить знаки правых частей ограничений;
- перейти от ограничений-неравенств к равенствам;
- избавиться от переменных, не имеющих ограничений на знак.
Для решения нашей задачи воспользуемся симплекс-методом, так как этот метод предназначен для решения задач линейного программирования любой размерности.
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
... имеет вид найти переменные задачи удовлетворяющие системе ограничений: и условию неотрицательности 0 (j = ), которая обеспечивает экстремум целевой функции Z(Y) = Допустимым решением задачи линейного программирования называется любой набор значений переменных удовлетворяющий системе ограничений и условной неотрицательности. Множество допустимых решений образует область допустимых ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...






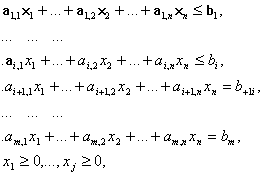
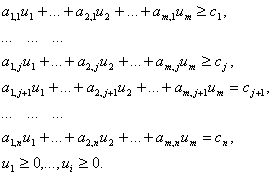
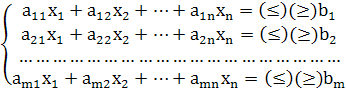
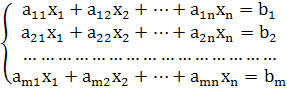



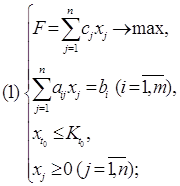
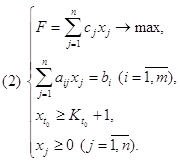
0 комментариев