Навигация
АНАЛИЗ НА ЧУВСТВИТЕЛЬНОСТЬ К ИЗМЕНЕНИЯМ КОЭФФИЦИЕНТОВ ЦЕЛЕВОЙ ФУНКЦИИ
5.4. АНАЛИЗ НА ЧУВСТВИТЕЛЬНОСТЬ К ИЗМЕНЕНИЯМ КОЭФФИЦИЕНТОВ ЦЕЛЕВОЙ ФУНКЦИИ
В данной задаче коэффициенты целевой функции имеют сложный физический смысл, поэтому анализ на чувствительность к изменению ее коэффициентов производить не будем.
6. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ЦЕЛОЧИСЛЕННОГО РЕШЕНИЯДанная задача по своему содержанию является частично целочисленной. Переменные X1 , X2 , X3 , X4 , X5 , X6 ,обозначающие время работы определенного станка над деталями определенного типа, должны принимать целые значения. В то же время, переменные Х7 , Х8, обозначающие время простоя соответственно токарного станка и станка-автомата, могут принимать дробные значения. Для поиска оптимального целочисленного решения воспользуемся методом Гомори для частично целочисленных задач.
6.1. МЕТОД ГОМОРИ ДЛЯ ЧАСТИЧНО ЦЕЛОЧИСЛЕННЫХ ЗАДАЧ
Метод Гомори для нахождения целочисленного решения относится к большой группе методов, называемых методами отсечений. Эти методы основаны на введении в задачу дополнительных ограничений, позволяющих учесть требование целочисленности. Основная идея методов отсечений состоит в том, что на полученное оптимальное нецелочисленное решение накладывается дополнительное ограничение, которое делает это решение недопустимым, но и не отсекает ни одного целочисленного решения от области допустимых решений.
Ограничения составляются по финальной симплекс-таблице, в которой получено оптимальное нецелочисленное решение. При этом на первоначальную систему ограничений накладывается новое ограничение по следующей формуле:
L1*W1 + L2*W2 + … +Ln*Wn ≥ {Bi} , где
![]() Aij, если Aij≥0 и Wj может быть дробной, (1)
Aij, если Aij≥0 и Wj может быть дробной, (1)
({Bi}*Aij)/({Bi}-1), если Aij<0 и Wj может быть дробной, (2)
Lj = {Aij}, если {Aij}£{Bi} и Wi должна быть целой, (3)
{Bi}*(1-{Aij})/(1-{Bi}), если {Aij}>{Bi} и Wi должна быть целой, (4)
j=1,…,n
где Wn – небазисная переменная;
Bi - базисная переменная, имеющая максимальную дробную часть ( дробная часть числа – это разность между этим числом и максимальным целым числом, не превосходящим его);
Aij – коэффициент, стоящий на пересечении строки i-ой базисной переменной и столбца j-ой небазисной переменной;
Далее полученное ограничение приводится к стандартному виду:
-L1*W1 - L2*W2 - … -Ln*Wn + Sr = -{Bi}
где r – номер итерации алгоритма.
Здесь Sr – неотрицательная остаточная переменная, не имеющая никакого содержательного смысла; в оптимальном целочисленном решении эта переменная оказывается равной нулю.
В нашем случае переменная, имеющая максимальную дробную часть – это Х4 ({2,67}=0,67), она должна быть целой, переменные Х7 и Х8 могут быть дробными, переменные Х1 и Х2 должны быть целыми, поэтому, согласно выше приведенной формуле, составим новое дополнительное ограничение. Так как все коэффициенты на пересечениях базисной переменной Х4 и небазисных переменных Х1 , Х2 , Х7 , Х8 ≥ 0 (0,44≥0, 0,11≥0, 0,17≥0), то коэффициенты при переменных Х1 и Х2 рассчитали по формуле (3): L1={0,44}=0,44, L2={0,11}=0,11, а коэффициенты при переменных Х7 и Х8 рассчитали по формуле (1): L3=0,17, L4=0,17. {В4}={Х4} = {2,67} = 0,67. Ограничение будет иметь вид:
0,44Х1 + 0,11Х2 + 0,17Х7 + 0,17Х8 ≥ 0,67
Можно убедиться, что это ограничение сделало наше оптимальное решение недопустимым ( если подставить Х1=0, Х2=0, Х7=0, Х8=0, - значения переменных, полученных в оптимальном нецелочисленном решении, то получим 0≥0,67 – неверно).
Приведя ограничение к стандартному виду, имеем:
-0,44Х1 - 0,11Х2 - 0,17Х7 - 0,17Х8 + Х9 = -0,67
Добавим к нашей финальной симлекс-таблице строку и столбец, соответствующие построенному ограничению и новой базисной переменной Х9:
| БП | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | БР |
| E | 1,67 | 1,67 | 0 | 0 | 0 | 0 | 2,5 | 2,5 | 0 | 40 |
| X3 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 8 |
| X6 | -0,67 | -0,67 | 0 | 0 | 0 | 1 | -0,5 | 0,5 | 0 | 0 |
| X4 | 0,44 | 0,11 | 0 | 1 | 0 | 0 | 0,17 | 0,17 | 0 | 2,67 |
| Х5 | 0,22 | 0,55 | 0 | 0 | 1 | 0 | 0,33 | 0,33 | 0 | 5,33 |
| X9 | -0,44 | -0,11 | 0 | 0 | 0 | 0 | -0,17 | -0,17 | 1 | -0,67 |
Таблица 8. Симплекс-таблица №7.
Как видно, полученная симплекс-таблица содержит недопустимое решение (переменная Х9 имеет отрицательное значение). Произведем дальнейший пересчет таблицы, причем ведущую строку определяем максимальным по модулю отрицательным элементом столбца решений, а ведущий столбец – минимальным по модулю отношением элемента Е-строки к отрицательным элементам ведущей строки. Пересчет симплекс-таблицы осуществляется на основе стандартных процедур симплекс-метода.
Итак, переменная, исключаемая из базиса – это X9, т.к. ее значение –0,67 - это максимальный по модулю отрицательный элемент столбца решений. В базис включаем переменную X1, т.к. |1,67/(-0,44)|=3,8, |1,67/(-0,11)|=15,2, |2,5/(-0,17)|=14,7, 3,8 – минимальное по модулю отношение элемента Е-строки к отрицательным элементам ведущей строки. Ведущий элемент равен –0,44. Получим новую симплекс-таблицу:
| БП | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | БР |
| E | 0 | 1,25 | 0 | 0 | 0 | 0 | 1,875 | 1,875 | 3,75 | 37,5 |
| X3 | 0 | 0,75 | 1 | 0 | 0 | 0 | 0,625 | -0,375 | 2,25 | 6,5 |
| X6 | 0 | -0,5 | 0 | 0 | 0 | 1 | -0,25 | 0,75 | -1,5 | 1 |
| X4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 2 |
| Х5 | 0 | 0,5 | 0 | 0 | 1 | 0 | 0,25 | 0,25 | 0,5 | 5 |
| X1 | 1 | 0,25 | 0 | 0 | 0 | 0 | 0,375 | 0,375 | -2,25 | 1,5 |
Таблица 9. Симплекс-таблица №8.
Все значения базисных переменных стали неотрицательными, это означает остановку вычислительного процесса на данной итерации и анализ полученных результатов. Как видно из таблицы, в базис вошла новая переменная Х1, переменные Х3, Х4 и Х5 уменьшили свое значение, а переменная Х6 увеличилась. Значение целевой функции уменьшилось и стало равно 37,5 , что объясняется тем, что оптимальное нецелочисленное решение было отсечено нашим дополнительным ограничением, и для поиска оптимального целочисленного решения мы ушли вглубь области допустимых решений, где значение целевой функции меньше оптимального. Наше решение все еще нецелочисленное, поэтому составим новое ограничение.
Переменная, имеющая максимальную дробную часть – это Х3 ({6,5}=0,5) (Х1 имеет такую же дробную часть, поэтому выбрали любую из них, например, Х3), она должна быть целой, переменные Х7 , Х8 и Х9 могут быть дробными, переменная Х2 должна быть целой, поэтому, согласно формуле, составим новое дополнительное ограничение. Так как коэффициенты на пересечениях базисной переменной Х3 и небазисных переменных Х2 , Х7 , Х9 ≥ 0 (0,75≥0, 0,625≥0, 2,25≥0), то коэффициент при переменной Х2 рассчитаем по формуле (3): L1={0,75}=0,75, коэффициенты при переменных Х7 и Х9 рассчитаем по формуле (1): L3=0,625, L4=2,25. Так как коэффициент на пересечении базисной переменной Х3 и небазисной переменной Х8<0, то коэффициент при переменной Х8 рассчитаем по формуле (2): L2=({6,5}*(-0,375))/({6,5}-1)=0,375. {В3}={Х3} = {6,5} = 0,5. Ограничение будет иметь вид:
0,25Х2 + 0,625Х7 + 0,375Х8 + 2,25Х9 ≥ 0,5
Или, после приведения к стандартному виду, получим:
-0,25Х2 – 0,625Х7 – 0,375Х8 – 2,25Х9 + Х10 = -0,5
Добавим это ограничение к нашей предыдущей симплекс-таблице:
| БП | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | БР |
| E | 0 | 1,25 | 0 | 0 | 0 | 0 | 1,875 | 1,875 | 3,75 | 0 | 37,5 |
| Х3 | 0 | 0,75 | 1 | 0 | 0 | 0 | 0,625 | -0,375 | 2,25 | 0 | 6,5 |
| X6 | 0 | -0,5 | 0 | 0 | 0 | 1 | -0,25 | 0,75 | -1,5 | 0 | 1 |
| X4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 2 |
| X5 | 1 | 0,5 | 0 | 0 | 1 | 0 | 0,2 | 0,25 | 0,5 | 0 | 5 |
| Х1 | 1 | 0,25 | 0 | 0 | 0 | 0 | 0,375 | 0,375 | -2,25 | 0 | 1,5 |
| X10 | 0 | -0,25 | 0 | 0 | 0 | 0 | -0,375 | -0,375 | -2,25 | 1 | -0,5 |
Таблица 10. Симплекс-таблица №9.
Переменная, исключаемая из базиса – это X10, т.к. ее значение –0,5 - это максимальный по модулю отрицательный элемент столбца решений. В базис включаем переменную X9, т.к. |3,75/(-2,25)|=1,67, |1,25/(-0,25)|=5, |1,875/(-0,375)|=5, 1,67 – минимальное по модулю отношение элемента Е-строки к отрицательным элементам ведущей строки. Ведущий элемент равен –2,25. Получим новую симплекс-таблицу:
| БП | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | БР |
| E | 0 | 0,83 | 0 | 0 | 0 | 0 | 1,25 | 1,25 | 0 | 1,67 | 36,67 |
| Х3 | 0 | 0,5 | 1 | 0 | 0 | 0 | 0,25 | -0,75 | 0 | 1 | 6 |
| X6 | 0 | -0,33 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | -0,67 | 1,33 |
| X4 | 0 | 0,111 | 0 | 1 | 0 | 0 | -0,17 | -0,17 | 0 | 0,44 | 1,78 |
| X5 | 0 | 0,444 | 0 | 0 | 1 | 0 | 0,17 | 0,17 | 0 | 0,22 | 4,89 |
| Х1 | 1 | 0,5 | 0 | 0 | 0 | 0 | 0,75 | 0,75 | 0 | -1 | 2 |
| X9 | 0 | 0,11 | 0 | 0 | 0 | 0 | 0,17 | 0,17 | 1 | -0,44 | 0,22 |
Таблица 11. Симплекс-таблица №10.
Решение все еще не целочисленное, поэтому переходим к следующей итерации. Переменная, имеющая максимальную дробную часть – это Х5 ({4,89}=0,89), она должна быть целой, переменные Х7 , Х8 и Х10 могут быть дробными, переменная Х2 должна быть целой, поэтому, согласно формуле, составим новое дополнительное ограничение. Так как коэффициенты на пересечениях базисной переменной Х5 и небазисных переменных Х2, X7, X8, Х10≥0 (0,44≥0, 0,17≥0, 0,22≥0), то коэффициент при переменной Х2 рассчитаем по формуле (3): L1={0,44}=0,44, коэффициенты при переменных Х7, Х9 и Х10 рассчитаем по формуле (1): L2=0,17, L3=0,17, L4=0,22. {В5}={Х5} = {4,89} = 0,89. Ограничение будет иметь вид:
0,44Х2 + 0,17Х7 + 0,17Х8 + 0,22Х10 ≥ 0,89
Или, после приведения к стандартному виду, получим:
-0,44Х2 – 0,17Х7 – 0,17Х8 – 0,22Х10 + Х11 = -0,89
Добавим это ограничение к нашей предыдущей симплекс-таблице:
| БП | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | Х11 | БР |
| E | 0 | 0,83 | 0 | 0 | 0 | 0 | 1,25 | 1,25 | 0 | 1,67 | 0 | 36,67 |
| Х3 | 0 | 0,5 | 1 | 0 | 0 | 0 | 0,25 | -0,75 | 0 | 1 | 0 | 6 |
| X6 | 0 | -0,3 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | -0,67 | 0 | 1,33 |
| X4 | 0 | 0,11 | 0 | 1 | 0 | 0 | -0,17 | -0,17 | 0 | 0,44 | 0 | 1,78 |
| X5 | 0 | 0,44 | 0 | 0 | 1 | 0 | 0,17 | 0,17 | 0 | 0,22 | 0 | 4,89 |
| Х1 | 1 | 0,5 | 0 | 0 | 0 | 0 | 0,75 | 0,75 | 0 | -1 | 0 | 2 |
| Х9 | 0 | 0,11 | 0 | 0 | 0 | 0 | 0,17 | 0,17 | 1 | -0,44 | 0 | 2 |
| X11 | 0 | -0,44 | 0 | 0 | 0 | 0 | -0,17 | -0,17 | 0 | -0,22 | 1 | -0,89 |
Таблица 12. Симплекс-таблица №11.
Переменная, исключаемая из базиса – это X11, т.к. ее значение –0,89 - это максимальный по модулю отрицательный элемент столбца решений. В базис включаем переменную X2, т.к. |0,83/(-0,44)|=1,9, |1,25/(-0,17)|=7,4, |1,67/(-0,22)|=7,6, 1,9 – минимальное по модулю отношение элемента Е-строки к отрицательным элементам ведущей строки. Ведущий элемент равен –0,44. После пересчетов получим получим новую симплекс-таблицу:
| БП | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | Х11 | БР |
| E | 0 | 0 | 0 | 0 | 0 | 0 | 0,938 | 0,94 | 0 | 1,25 | 1,89 | 35 |
| Х3 | 0 | 0 | 1 | 0 | 0 | 0 | 0,063 | -0,938 | 0 | 0,75 | 1,125 | 5 |
| X6 | 0 | 0 | 0 | 0 | 0 | 1 | 0,125 | 1,125 | 0 | -0,5 | -0,75 | 2 |
| X4 | 0 | 0 | 0 | 1 | 0 | 0 | -0,125 | -0,125 | 0 | 0,5 | -0,25 | 2 |
| X5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 4 |
| Х1 | 1 | 0 | 0 | 0 | 0 | 0 | 0,563 | 0,563 | 0 | -1,25 | 1,125 | 1 |
| Х9 | 0 | 0 | 0 | 0 | 0 | 0 | 0,125 | 0,125 | 1 | -0,5 | 0,25 | 0 |
| X2 | 0 | 1 | 0 | 0 | 0 | 0 | 0,375 | 0,375 | 0 | 0,5 | -2,25 | 2 |
Таблица 13. Симплекс-таблица №12.
Столбец решений не содержит отрицательных элементов, все переменные X1, X2, X3 , X4 , X5 , X6 приняли целочисленные значения, значит, оптимальное целочисленное решение найдено, оно равно: (X1,X2,X3,X4,X5,X6)=(1,2,5,2,4,2), целевая функция при этом принимает максимальное значение: Е=35.
ЗАКЛЮЧЕНИЕ
После проведенных вычислений, решив задачу оптимизации, мы получили следующие результаты: оптимальный план работы станков состоит в том, чтобы токарный станок работал 1 час над деталями типа 1, 2 часа над деталями типа 2 и 5 часов над деталями типа 3 за смену; станок-автомат должен работать 2 часа над деталями типа 1 , 4 часа над деталями типа 2 и 2 часа над деталями типа 3 за смену. При этом количество комплектов деталей, выпускаемых цехом, будет максимально и равно 35.
В результате проведенного анализа на чувствительность к изменению запаса времени работы токарного станка получили, что если запас времени работы этого станка будет находиться в пределах от 0 до 8 часов, то базис оптимального решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5).
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995.
2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.2. – Мн.: БГУИР, 1996.
3. Смородинский С.С., Батин Н.В. Анализ и оптимизация систем на основе аналитических моделей. - Мн.: БГУИР, 1997.
4. Дегтярев Ю.И. Исследование операций. - М.: Высшая школа, 1986.
УСЛОВНЫЕ СОКРАЩЕНИЯ
БР – базисное решение
БП – базисная переменная
Условие задачи. Приложение.
+-----------------------------------------------------------------------+
¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦Вид огр.¦Значение¦
+--------+--------+--------+--------+--------+--------+--------+--------¦
¦ -1.00¦ -1.00¦ -2.00¦ -3.00¦ -3.00¦ -2.00¦ E ¦ ¦
+--------+--------+--------+--------+--------+--------+--------+--------¦
¦ 2.00¦ -1.00¦ 0.00¦ 6.00¦ -3.00¦ 0.00¦ == ¦ 0.00¦
¦ 2.00¦ 0.00¦ -2.00¦ 6.00¦ 0.00¦ -2.00¦ == ¦ 0.00¦
¦ 1.00¦ 1.00¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ <= ¦ 8.00¦
¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ 1.00¦ 1.00¦ <= ¦ 8.00¦
+-----------------------------------------------------------------------+
Вывод промежуточных результатов оптимизации.
+----------------------------------------------------------------------------------------------------------+
¦ N¦ БП ¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦ X7 ¦ X8 ¦ X9 ¦ X10 ¦Баз.Реш.¦
+--+----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+---
¦ 1¦ E ¦ -1.00¦ -1.00¦ -2.00¦ -3.00¦ -3.00¦ -2.00¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+---
¦ ¦ -W ¦ -4.00¦ 1.00¦ 2.00¦ -12.00¦ 3.00¦ 2.00¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+--
¦ ¦ X9 ¦ 2.00¦ -1.00¦ 0.00¦ 6.00¦ -3.00¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.00¦
¦ ¦ X10¦ 2.00¦ 0.00¦ -2.00¦ 6.00¦ 0.00¦ -2.00¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦
¦ ¦ X7 ¦ 1.00¦ 1.00¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 8.00¦
¦ ¦ X8 ¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ 1.00¦ 1.00¦ 0.00¦ 1.00¦ 0.00¦ 0.00¦ 8.00¦
+----------------------------------------------------------------------------------------------------------+
Ведущий элемент находится в 4 столбце и 1 строке.
Вывод промежуточных результатов оптимизации.
+----------------------------------------------------------------------------------------------------------+
¦ N¦ БП ¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦ X7 ¦ X8 ¦ X9 ¦ X10 ¦Баз.Реш.¦
+--+----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+--
¦ 2¦ E ¦ 0.00¦ -1.50¦ -2.00¦ 0.00¦ -4.50¦ -2.00¦ 0.00¦ 0.00¦ 0.50¦ 0.00¦ 0.00¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+-
¦ ¦ -W ¦ 0.00¦ -1.00¦ 2.00¦ 0.00¦ -3.00¦ 2.00¦ 0.00¦ 0.00¦ 2.00¦ 0.00¦ 0.00¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+
¦ ¦ X4 ¦ 0.33¦ -0.17¦ 0.00¦ 1.00¦ -0.50¦ 0.00¦ 0.00¦ 0.00¦ 0.17¦ 0.00¦ 0.00¦
¦ ¦ X10¦ 0.00¦ 1.00¦ -2.00¦ 0.00¦ 3.00¦ -2.00¦ 0.00¦ 0.00¦ -1.00¦ 1.00¦ 0.00¦
¦ ¦ X7 ¦ 1.00¦ 1.00¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 8.00¦
¦ ¦ X8 ¦ -0.33¦ 0.17¦ 0.00¦ 0.00¦ 1.50¦ 1.00¦ 0.00¦ 1.00¦ -0.17¦ 0.00¦ 8.00¦
+----------------------------------------------------------------------------------------------------------+
Ведущий элемент находится в 5 столбце и 2 строке.
Вывод промежуточных результатов оптимизации.
+----------------------------------------------------------------------------------------------------------+
¦ N¦ БП ¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦ X7 ¦ X8 ¦ X9 ¦ X10 ¦Баз.Реш.¦
+--+----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+--
¦ 3¦ E ¦ 0.00¦ 0.00¦ -5.00¦ 0.00¦ 0.00¦ -5.00¦ 0.00¦ 0.00¦ -1.00¦ 1.50¦ 0.00¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+
¦ ¦ -W ¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ 1.00¦ 0.00¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+
¦ ¦ X4 ¦ 0.33¦ 0.00¦ -0.33¦ 1.00¦ 0.00¦ -0.33¦ 0.00¦ 0.00¦ 0.00¦ 0.17¦ 0.00¦
¦ ¦ X5 ¦ 0.00¦ 0.33¦ -0.67¦ 0.00¦ 1.00¦ -0.67¦ 0.00¦ 0.00¦ -0.33¦ 0.33¦ 0.00¦
¦ ¦ X7 ¦ 1.00¦ 1.00¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 8.00¦
¦ ¦ X8 ¦ -0.33¦ -0.33¦ 1.00¦ 0.00¦ 0.00¦ 2.00¦ 0.00¦ 1.00¦ 0.33¦ -0.50¦ 8.00¦
+----------------------------------------------------------------------------------------------------------+
Вывод промежуточных результатов оптимизации.
+----------------------------------------------------------------------------------------+
¦ N¦ БП ¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦ X7 ¦ X8 ¦Баз.Реш.¦
+--+----+--------+--------+--------+--------+--------+--------+--------+--------+---
¦ 3¦ E ¦ 0.00¦ 0.00¦ -5.00¦ 0.00¦ 0.00¦ -5.00¦ 0.00¦ 0.00¦ 0.00¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+-
¦ ¦ X4 ¦ 0.33¦ 0.00¦ -0.33¦ 1.00¦ 0.00¦ -0.33¦ 0.00¦ 0.00¦ 0.00¦
¦ ¦ X5 ¦ 0.00¦ 0.33¦ -0.67¦ 0.00¦ 1.00¦ -0.67¦ 0.00¦ 0.00¦ 0.00¦
¦ ¦ X7 ¦ 1.00¦ 1.00¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 8.00¦
¦ ¦ X8 ¦ -0.33¦ -0.33¦ 1.00¦ 0.00¦ 0.00¦ 2.00¦ 0.00¦ 1.00¦ 8.00¦
+----------------------------------------------------------------------------------------+
Ведущий элемент находится в 3 столбце и 3 строке.
Вывод промежуточных результатов оптимизации.
+----------------------------------------------------------------------------------------+
¦ N¦ БП ¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦ X7 ¦ X8 ¦Баз.Реш.¦
+--+----+--------+--------+--------+--------+--------+--------+--------+--------+---
¦ 4¦ E ¦ 5.00¦ 5.00¦ 0.00¦ 0.00¦ 0.00¦ -5.00¦ 5.00¦ 0.00¦ 40.00¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--
¦ ¦ X4 ¦ 0.67¦ 0.33¦ 0.00¦ 1.00¦ 0.00¦ -0.33¦ 0.33¦ 0.00¦ 2.67¦
¦ ¦ X5 ¦ 0.67¦ 1.00¦ 0.00¦ 0.00¦ 1.00¦ -0.67¦ 0.67¦ 0.00¦ 5.33¦
¦ ¦ X3 ¦ 1.00¦ 1.00¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 8.00¦
¦ ¦ X8 ¦ -1.33¦ -1.33¦ 0.00¦ 0.00¦ 0.00¦ 2.00¦ -1.00¦ 1.00¦ 0.00¦
+----------------------------------------------------------------------------------------+
Ведущий элемент находится в 6 столбце и 4 строке.
Вывод промежуточных результатов оптимизации.
+----------------------------------------------------------------------------------------+
¦ N¦ БП ¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦ X7 ¦ X8 ¦Баз.Реш.¦
+--+----+--------+--------+--------+--------+--------+--------+--------+--------+---
¦ 5¦ E ¦ 1.67¦ 1.67¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 2.50¦ 2.50¦ 40.00¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--
¦ ¦ X4 ¦ 0.44¦ 0.11¦ 0.00¦ 1.00¦ 0.00¦ 0.00¦ 0.17¦ 0.17¦ 2.67¦
¦ ¦ X5 ¦ 0.22¦ 0.56¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.33¦ 0.33¦ 5.33¦
¦ ¦ X3 ¦ 1.00¦ 1.00¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 8.00¦
¦ ¦ X6 ¦ -0.67¦ -0.67¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ -0.50¦ 0.50¦ 0.00¦
+----------------------------------------------------------------------------------------+
Результаты оптимизации.
Базис Значение
X4 2.67
X5 5.33
X3 8.00
X6 0.00
Максимум функции равен 40.00
Вывод промежуточных результатов оптимизации.
+-------------------------------------------------------------------------------------------------+
¦ N¦ БП ¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦ X7 ¦ X8 ¦ X9 ¦Баз.Реш.¦
+--+----+--------+--------+--------+--------+--------+--------+--------+--------+--------+---
¦ 1¦ E ¦ 1.67¦ 1.67¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 2.50¦ 2.50¦ 0.00¦ 40.00¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--------+-
¦ ¦ X4 ¦ 0.44¦ 0.11¦ 0.00¦ 1.00¦ 0.00¦ 0.00¦ 0.17¦ 0.17¦ 0.00¦ 2.67¦
¦ ¦ X5 ¦ 0.22¦ 0.56¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.33¦ 0.33¦ 0.00¦ 5.33¦
¦ ¦ X3 ¦ 1.00¦ 1.00¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.00¦ 8.00¦
¦ ¦ X6 ¦ -0.67¦ -0.67¦ 0.00¦ 0.00¦ 0.00¦ 1.00¦ -0.50¦ 0.50¦ 0.00¦ 0.00¦
¦ ¦ X9 ¦ -0.44¦ -0.11¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ -0.17¦ -0.17¦ 1.00¦ -0.67¦
+-------------------------------------------------------------------------------------------------+
Ведущий элемент находится в 1 столбце и 5 строке.
Вывод промежуточных результатов оптимизации.
+-------------------------------------------------------------------------------------------------+
¦ N¦ БП ¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦ X7 ¦ X8 ¦ X9 ¦Баз.Реш.¦
+--+----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--
¦ 2¦ E ¦ -0.00¦ 1.25¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 1.88¦ 1.88¦ 3.75¦ 37.50¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--
¦ ¦ X4 ¦ -0.00¦ -0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.00¦ -0.00¦ -0.00¦ 1.00¦ 2.00¦
¦ ¦ X5 ¦ -0.00¦ 0.50¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.25¦ 0.25¦ 0.50¦ 5.00¦
¦ ¦ X3 ¦ -0.00¦ 0.75¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 0.62¦ -0.38¦ 2.25¦ 6.50¦
¦ ¦ X6 ¦ -0.00¦ -0.50¦ -0.00¦ -0.00¦ -0.00¦ 1.00¦ -0.25¦ 0.75¦ -1.50¦ 1.00¦
¦ ¦ X1 ¦ 1.00¦ 0.25¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ 0.38¦ 0.38¦ -2.25¦ 1.50¦
+-------------------------------------------------------------------------------------------------+
Результаты оптимизации.
Базис Значение
X4 2.00
X5 5.00
X3 6.50
X6 1.00
X1 1.50
Максимум функции равен 37.50
Вывод промежуточных результатов оптимизации.
+----------------------------------------------------------------------------------------------------------+
¦ N¦ БП ¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦ X7 ¦ X8 ¦ X9 ¦ X10 ¦Баз.Реш.¦
+--+----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+--
¦ 2¦ E ¦ -0.00¦ 1.25¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 1.88¦ 1.88¦ 3.75¦ 0.00¦ 37.50¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+-
¦ ¦ X4 ¦ -0.00¦ -0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.00¦ -0.00¦ -0.00¦ 1.00¦ 0.00¦ 2.00¦
¦ ¦ X5 ¦ -0.00¦ 0.50¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.25¦ 0.25¦ 0.50¦ 0.00¦ 5.00¦
¦ ¦ X3 ¦ -0.00¦ 0.75¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 0.62¦ -0.38¦ 2.25¦ 0.00¦ 6.50¦
¦ ¦ X6 ¦ -0.00¦ -0.50¦ -0.00¦ -0.00¦ -0.00¦ 1.00¦ -0.25¦ 0.75¦ -1.50¦ 0.00¦ 1.00¦
¦ ¦ X1 ¦ 1.00¦ 0.25¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ 0.38¦ 0.38¦ -2.25¦ 0.00¦ 1.50¦
¦ ¦ X10¦ 0.00¦ -0.25¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ -0.38¦ -0.38¦ -2.25¦ 1.00¦ -0.50¦
+----------------------------------------------------------------------------------------------------------+
Ведущий элемент находится в 9 столбце и 6 строке.
Вывод промежуточных результатов оптимизации.
+----------------------------------------------------------------------------------------------------------+
¦ N¦ БП ¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦ X7 ¦ X8 ¦ X9 ¦ X10 ¦Баз.Реш.¦
+--+----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+--
¦ 3¦ E ¦ -0.00¦ 0.83¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 1.25¦ 1.25¦ -0.00¦ 1.67¦ 36.67¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+-
¦ ¦ X4 ¦ -0.00¦ -0.11¦ 0.00¦ 1.00¦ 0.00¦ 0.00¦ -0.17¦ -0.17¦ -0.00¦ 0.44¦ 1.78¦
¦ ¦ X5 ¦ -0.00¦ 0.44¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.17¦ 0.17¦ -0.00¦ 0.22¦ 4.89¦
¦ ¦ X3 ¦ -0.00¦ 0.50¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 0.25¦ -0.75¦ -0.00¦ 1.00¦ 6.00¦
¦ ¦ X6 ¦ -0.00¦ -0.33¦ -0.00¦ -0.00¦ -0.00¦ 1.00¦ -0.00¦ 1.00¦ -0.00¦ -0.67¦ 1.33¦
¦ ¦ X1 ¦ 1.00¦ 0.50¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ 0.75¦ 0.75¦ -0.00¦ -1.00¦ 2.00¦
¦ ¦ X9 ¦ -0.00¦ 0.11¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ 0.17¦ 0.17¦ 1.00¦ -0.44¦ 0.22¦
+----------------------------------------------------------------------------------------------------------+
Результаты оптимизации.
Базис Значение
X4 1.78
X5 4.89
X3 6.00
X6 1.33
X1 2.00
X9 0.22
Максимум функции равен 36.67
Вывод промежуточных результатов оптимизации.
+-------------------------------------------------------------------------------------------------------------------+
¦ N¦ БП ¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦ X7 ¦ X8 ¦ X9 ¦ X10 ¦ X11 ¦Баз.Реш.¦
+--+----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+--
¦ 3¦ E ¦ -0.00¦ 0.83¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 1.25¦ 1.25¦ -0.00¦ 1.67¦ 0.00¦ 36.67¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+-
¦ ¦ X4 ¦ -0.00¦ -0.11¦ 0.00¦ 1.00¦ 0.00¦ 0.00¦ -0.17¦ -0.17¦ -0.00¦ 0.44¦ 0.00¦ 1.78¦
¦ ¦ X5 ¦ -0.00¦ 0.44¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ 0.17¦ 0.17¦ -0.00¦ 0.22¦ 0.00¦ 4.89¦
¦ ¦ X3 ¦ -0.00¦ 0.50¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 0.25¦ -0.75¦ -0.00¦ 1.00¦ 0.00¦ 6.00¦
¦ ¦ X6 ¦ -0.00¦ -0.33¦ -0.00¦ -0.00¦ -0.00¦ 1.00¦ -0.00¦ 1.00¦ -0.00¦ -0.67¦ 0.00¦ 1.33¦
¦ ¦ X1 ¦ 1.00¦ 0.50¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ 0.75¦ 0.75¦ -0.00¦ -1.00¦ 0.00¦ 2.00¦
¦ ¦ X9 ¦ -0.00¦ 0.11¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ 0.17¦ 0.17¦ 1.00¦ -0.44¦ 0.00¦ 0.22¦
¦ ¦ X11¦ 0.00¦ -0.44¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ -0.17¦ -0.17¦ 0.00¦ -0.22¦ 1.00¦ -0.89¦
+-------------------------------------------------------------------------------------------------------------------+
Ведущий элемент находится в 2 столбце и 7 строке.
Вывод промежуточных результатов оптимизации.
+-------------------------------------------------------------------------------------------------------------------+
¦ N¦ БП ¦ X1 ¦ X2 ¦ X3 ¦ X4 ¦ X5 ¦ X6 ¦ X7 ¦ X8 ¦ X9 ¦ X10 ¦ X11 ¦Баз.Реш.¦
+--+----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+--
¦ 4¦ E ¦ -0.00¦ -0.00¦ 0.00¦ 0.00¦ 0.00¦ 0.00¦ 0.94¦ 0.94¦ -0.00¦ 1.25¦ 1.88¦ 35.00¦
¦ +----+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+--------+
¦ ¦ X4 ¦ -0.00¦ -0.00¦ -0.00¦ 1.00¦ -0.00¦ -0.00¦ -0.12¦ -0.12¦ -0.00¦ 0.50¦ -0.25¦ 2.00¦
¦ ¦ X5 ¦ -0.00¦ -0.00¦ 0.00¦ 0.00¦ 1.00¦ 0.00¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ 1.00¦ 4.00¦
¦ ¦ X3 ¦ -0.00¦ -0.00¦ 1.00¦ 0.00¦ 0.00¦ 0.00¦ 0.06¦ -0.94¦ -0.00¦ 0.75¦ 1.13¦ 5.00¦
¦ ¦ X6 ¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ 1.00¦ 0.12¦ 1.12¦ -0.00¦ -0.50¦ -0.75¦ 2.00¦
¦ ¦ X1 ¦ 1.00¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ 0.56¦ 0.56¦ -0.00¦ -1.25¦ 1.12¦ 1.00¦
¦ ¦ X9 ¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ 0.12¦ 0.12¦ 1.00¦ -0.50¦ 0.25¦ 0.00¦
¦ ¦ X2 ¦ -0.00¦ 1.00¦ -0.00¦ -0.00¦ -0.00¦ -0.00¦ 0.38¦ 0.38¦ -0.00¦ 0.50¦ -2.25¦ 2.00¦
+-------------------------------------------------------------------------------------------------------------------+
Результаты оптимизации.
Базис Значение
X4 2.00
X5 4.00
X3 5.00
X6 2.00
X1 1.00
X9 0.00
X2 2.00
Максимум функции равен 35.00
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
... имеет вид найти переменные задачи удовлетворяющие системе ограничений: и условию неотрицательности 0 (j = ), которая обеспечивает экстремум целевой функции Z(Y) = Допустимым решением задачи линейного программирования называется любой набор значений переменных удовлетворяющий системе ограничений и условной неотрицательности. Множество допустимых решений образует область допустимых ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...






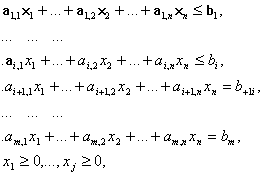
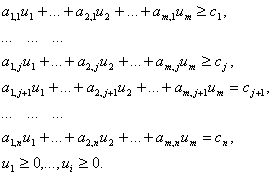
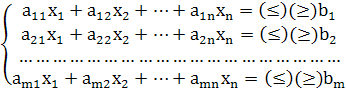
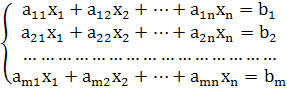



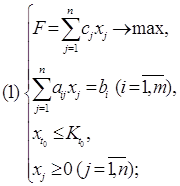
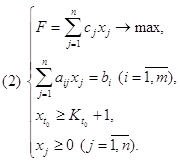
0 комментариев