ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ
ОСНОВНАЯ ИДЕЯ СИМПЛЕКС-МЕТОДА
ПОСТРОЕНИЕ ИСКУССТВЕННОГО БАЗИСА
Реализуем
первый этап двухэтапного метода: с помощью процедур симплекс-
ВТОРОЙ ЭТАП ДВУХЭТАПНОГО СИМЛЕКС-МЕТОДА
АНАЛИЗ МОДЕЛИ НА ЧУВСТВИТЕЛЬНОСТЬ
АНАЛИЗ НА ЧУВСТВИТЕЛЬНОСТЬ К ИЗМЕНЕНИЯМ КОЭФФИЦИЕНТОВ ЦЕЛЕВОЙ ФУНКЦИИ
Навигация
Реализуем первый этап двухэтапного метода: с помощью процедур симплекс-
Решение оптимизационной задачи линейного программирования
59893
знака
13
таблиц
0
изображений
6. Реализуем первый этап двухэтапного метода: с помощью процедур симплекс-
метода выполняем максимизацию функции -W. При этом переменные, включаемые в базис, выбираются по W-строке (т.е. на каждом цикле в базис включается переменная, которой соответствует максимальный по модулю отрицательный элемент в W-строке; столбец, соответствующий этой переменной, становится ведущим). В нашем случае это столбец X4, т. к. коэффициент при этой переменной в W-строке равен –12. Ведущую строку определяем следующим образом: рассчитываем так называемые симплексные отношения, т. е. отношения текущих значений базисных переменных к положительным коэффициентам ведущего столбца, соответствующим данным базисным переменным. Затем берем минимальное из этих отношений и по тому, какой строке оно соответствует, определяем ведущую строку. У нас есть три таких отношения: по переменной Х8 (8/1=8), Х9 (0/6=0) и Х10 (0/6=0). Получилось два минимальных значения, значит, возьмем любое из них, например по переменной Х9. После находим ведущий элемент, он расположен на пересечении ведущей строки и ведущего столбца (в нашем случае он равен 6). Затем определяем переменные, которые будем исключать из базиса и включать в него. Переменную, которой соответствует ведущий столбец, будем включать в базис вместо переменной, которой соответствует ведущая строка. Далее все преобразования выполняем по обычным формулам симплекс-метода или по "правилу прямоугольника". Преобразованиям подвергается вся симплекс-таблица, включая E-строку, W-строку и столбец решений. Получаем новую симплекс-таблицу:
| БП | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | БР |
| E | 0 | -1,5 | -2 | 0 | -4,5 | -2 | 0 | 0 | 0,5 | 0 | 0 |
| -W | 0 | -1 | 2 | 0 | -3 | 2 | 0 | 0 | 2 | 0 | 0 |
| X7 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 8 |
| X8 | -0,33 | 0,17 | 0 | 0 | 1,5 | 1 | 0 | 1 | -0,17 | 0 | 8 |
| X4 | 0,33 | -0,17 | 0 | 1 | -0,5 | 0 | 0 | 0 | 0,17 | 0 | 0 |
| X10 | 0 | 1 | -2 | 0 | 3 | -2 | 0 | 0 | -1 | 1 | 0 |
Таблица 3. Симплекс-таблица №2.
Мы получили новое решение (Х7,Х8,Х4,Х10)=(8,8,0,0). Это решение недопустимо, так как в базисе содержится искусственная переменная Х10. Выполим очередную итерацию. По строке –W для включения в базис выбираем переменную X5 (т.к. –3 – максимальное по модулю отрицательное число). Столбец X5 становится ведущим. По минимальному симплексному отношению ( 8/1,5=5,33; 0/3=0) для исключения из базиса выбираем переменную Х10. Ведущий элемент равен 3. После проведенных пересчетов получаем новую симплекс-таблицу:
| БП | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | БР |
| E | 0 | 0 | -5 | 0 | 0 | -5 | 0 | 0 | -1 | 1,5 | 0 |
| -W | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| X7 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 8 |
| X8 | -0,33 | -0,33 | 1 | 0 | 0 | 2 | 0 | 1 | 0,33 | -0,5 | 8 |
| X4 | 0,33 | 0 | -0,33 | 1 | 0 | -0.33 | 0 | 0 | 0 | 0,17 | 0 |
| X5 | 0 | 0,33 | -0,67 | 0 | 1 | -0,67 | 0 | 0 | -0,33 | 0,33 | 0 |
Таблица 4. Симплекс-таблица №3.
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
... имеет вид найти переменные задачи удовлетворяющие системе ограничений: и условию неотрицательности 0 (j = ), которая обеспечивает экстремум целевой функции Z(Y) = Допустимым решением задачи линейного программирования называется любой набор значений переменных удовлетворяющий системе ограничений и условной неотрицательности. Множество допустимых решений образует область допустимых ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
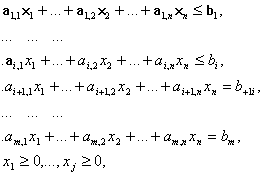
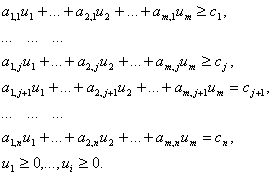
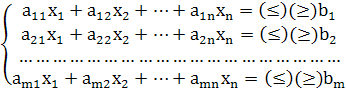
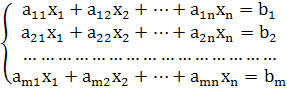
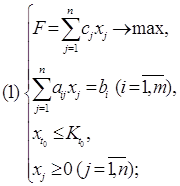
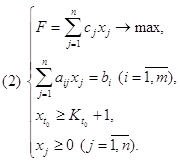
0 комментариев