ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ
ОСНОВНАЯ ИДЕЯ СИМПЛЕКС-МЕТОДА
ПОСТРОЕНИЕ ИСКУССТВЕННОГО БАЗИСА
Реализуем
первый этап двухэтапного метода: с помощью процедур симплекс-
ВТОРОЙ ЭТАП ДВУХЭТАПНОГО СИМЛЕКС-МЕТОДА
АНАЛИЗ МОДЕЛИ НА ЧУВСТВИТЕЛЬНОСТЬ
АНАЛИЗ НА ЧУВСТВИТЕЛЬНОСТЬ К ИЗМЕНЕНИЯМ КОЭФФИЦИЕНТОВ ЦЕЛЕВОЙ ФУНКЦИИ
Навигация
ВТОРОЙ ЭТАП ДВУХЭТАПНОГО СИМЛЕКС-МЕТОДА
Решение оптимизационной задачи линейного программирования
59893
знака
13
таблиц
0
изображений
4.5. ВТОРОЙ ЭТАП ДВУХЭТАПНОГО СИМЛЕКС-МЕТОДА
Итак, как видно из Таблицы 4, все искусственные переменные вышли из базиса, искусственная целевая функция обнулилась – значит, первый этап двухэтапного симплекс-метода закончен, найдено начальное допустимое решение: (Х1,X2,X3,X4,X5,X6) = (0,0,0,0,0,0), целевая функция Е=0. Теперь переходим к реализации второго этапа: вычеркиваем из таблицы строку искусственной целевой функции и столбцы искусственных переменных; над новой таблицей выполняем обычные процедуры симплекс-метода, а именно: ведущий столбец определяется также, как и для первого этапа двухэтапного симплекс-метода, единственное различие состоит в том, что максимальный по модулю отрицательный коэффициент находим по Е-строке целевой функции. Расчет ведем до тех пор, пока в Е-строке не останется отрицательных коэффициентов:
| БП | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | БР |
| E | 0 | 0 | -5 | 0 | 0 | -5 | 0 | 0 | 0 |
| X7 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 8 |
| X8 | -0,33 | -0,33 | 1 | 0 | 0 | 2 | 0 | 1 | 8 |
| X4 | 0,33 | 0 | -0,33 | 1 | 0 | -0,33 | 0 | 0 | 0 |
| X5 | 0 | 0,33 | -0,67 | 0 | 1 | -0,67 | 0 | 0 | 0 |
Таблица 5. Симплекс-таблица №4.
Наше начальное допустимое решение не является оптимальным, так как в Е-строке содержатся отрицательные коэффициенты. Определим по Е-строке новую переменную для включения в базис. Это переменная X3, т.к. –5 – максимальное по модулю отрицательное число (коэффициент Е-строки при переменной X6 также равен –5, поэтому выбрали любую из этих переменных, например X3). Столбец X3 становится ведущим. По минимальному симплексному отношению ( 8/1=8; 8/1=8) для исключения из базиса выбираем переменную Х7 (симплексное отношение при переменной X8 также равно 8, поэтому выбрали любую из этих переменных). Ведущий элемент равен 1. После проведенных пересчетов получаем новую симплекс-таблицу:
| БП | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | БР |
| E | 5 | 5 | 0 | 0 | 0 | -5 | 5 | 0 | 40 |
| X3 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 8 |
| X8 | -1,33 | -1,33 | 0 | 0 | 0 | 2 | -1 | 1 | 0 |
| X4 | 0,67 | 0,33 | 0 | 1 | 0 | -0,33 | 0,33 | 0 | 2,67 |
| X5 | 0,67 | 1 | 0 | 0 | 1 | -0,67 | 0,67 | 0 | 5,33 |
Таблица 6. Симплекс-таблица №5.
Итак, как видно из таблицы, некоторые из искомых переменных , а именно Х3, Х4 и Х5, начали расти, что привело и к росту значения целевой функции – из нулевого значения она приняла значение 40. Это можно объяснить тем, что из точки начального допустимого решения мы перешли к соседней угловой точке области допустимых решений, причем в этой соседней точке рост целевой функции максимален. Однако в Е-строке есть еще отрицательный коэффициент, поэтому продолжим расчеты.
Определим по Е-строке новую переменную для включения в базис. Это переменная X6, т.к. –5 – максимальное по модулю отрицательное число. Столбец X6 становится ведущим. По минимальному симплексному отношению ( 0/2=0) для исключения из базиса выбираем переменную Х8. Получаем новую симплекс-таблицу:
| БП | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | БР |
| E | 1,67 | 1,67 | 0 | 0 | 0 | 0 | 2,5 | 2,5 | 40 |
| X3 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 8 |
| X6 | -0,67 | -0,67 | 0 | 0 | 0 | 1 | -0,5 | 0,5 | 0 |
| X4 | 0,44 | 0,11 | 0 | 1 | 0 | 0 | 0,17 | 0,17 | 2,67 |
| X5 | 0,22 | 0,55 | 0 | 0 | 1 | 0 | 0,33 | 0,33 | 5,33 |
Таблица 7. Симплекс-таблица №6.
Так как все коэффициенты E-строки таблицы 7 положительные, то оптимальное решение найдено. Оптимальный план состоит в том, чтобы токарный станок работал над деталями типа 3 8 часов за смену, то есть всю рабочую смену, и не работал над деталями типа 1 и 2 вообще. Станок-автомат должен работать за смену 2,67 часа над деталями типа 1 и 5,33 часа над деталями типа 2 и не должен работать над деталями типа 3. При этом за смену будет выпускаться максимально возможное количество комплектов деталей, а именно 40 комплектов. Ни один из станков не будет простаивать.
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
... имеет вид найти переменные задачи удовлетворяющие системе ограничений: и условию неотрицательности 0 (j = ), которая обеспечивает экстремум целевой функции Z(Y) = Допустимым решением задачи линейного программирования называется любой набор значений переменных удовлетворяющий системе ограничений и условной неотрицательности. Множество допустимых решений образует область допустимых ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
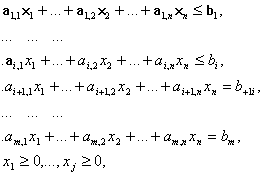
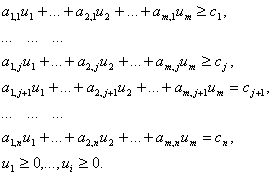
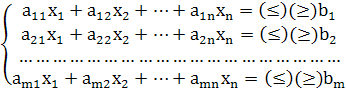
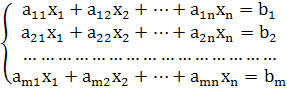
0 комментариев