Общая задача управляемости. Теорема об управляемости

16. Общая задача управляемости. Теорема об управляемости.

Рассмотрим вопрос: «Оптимален ли объект?»

Рассматриваем динамический объект, поведение которого описывается системой (1) , x- n-мерный вектор, , A-матрица nxn, u имеет ту же размерность, что и , .Задано , u: I и полагается, что u(t) измеримо и - где k(t) скалярная функция интегрируемая по Лебегу на отрезке I .Функция u(t)- называется допустимым управлением, если измерима и является однозначной ветвью из многозначного отображения U (2) u(t)U(t)- ограничения на управления . В фазовом пространстве заданы два не пустых множества. Допустимое управление u(t) на отр.I осуществляете переход из начального мн-ва в конечное множество , если существует решение уравнения (1), удовлетворяющее граничным условиям (4) и . Цель управления- перевод динамический объекта из в , а качество определяет функционал. Таким функционалом явл. время, следовательно

задача быстродействия заключается в нахождении такого допустимого управления, которое осуществляет переход из множества в за наименьшее время. (4).

Задача управления- решение вопроса : существует хотя бы одно допустимое управление u(t) , переводящий динамический объекта из в , на отр. времени I. Это соответствует решению краевой задачи: , .

Определим таким образом.

Теорема об уравляемости.Если и выпуклы, то объект явл. управляемым на отр. I из мн-ва в , тогда и только тогда, когда для

Док-во: Очевидно, объект управляем тогда и только тогда, когда множество достижимости и пересекаются. Т.к. и

выпуклы, то для него применим следствие из 11 св-ва опорных фун-ий ().

,;

;

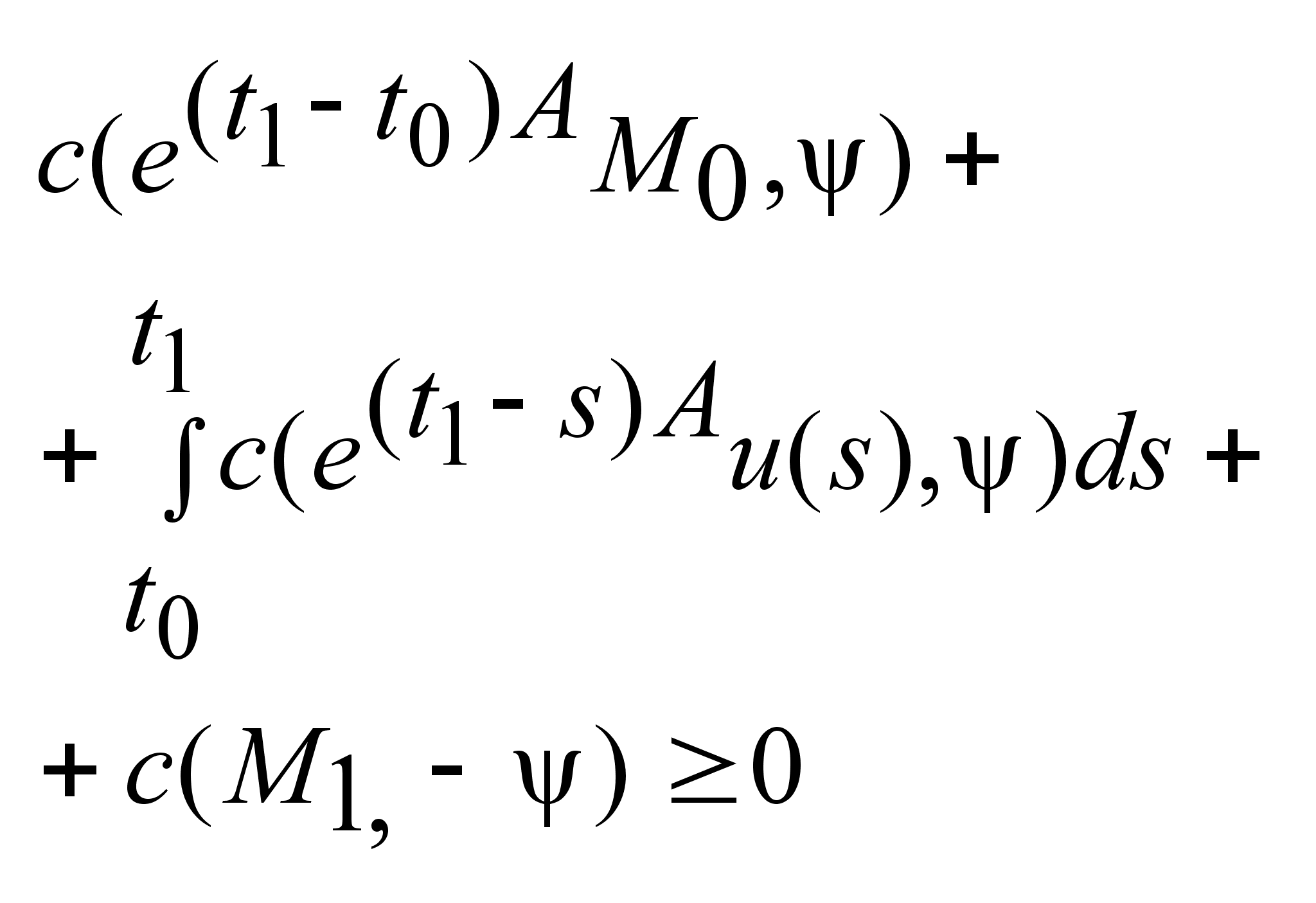Bocпользуемся еще одним св-ом опрных функий: если - невырожденная матрица, то можно воспользоваться св-вом , что :

.

В силу положительной опорной фун-ии относительно аргумента , получаем, что это верно .

Теорема док-на, т.к. левая часть неравенства и есть .

17.Численное решение задачи управляемости.

Объект управляем на I=, если выполняется . Если множнство ,, таковы что аналитически невозможно получить значение опорной функции u

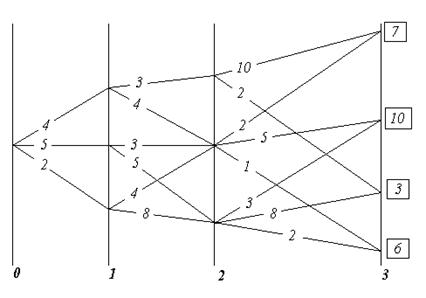
Вычисление матрицы и интеграл, тогда задача решается с применением ЭВМ. На ЭВМ решается для конечного числа . Для этого сфера покрывается -сетью. В двумерном пространстве -сеть определяется углом . В трехмерном пространстве -сеть определяется двумя углами. Пусть некоторая -сеть некоторой единичной сферы S, где -конечное множество. Какой бы вектор , найдется , такой что . Пусть вычислимое приближенное значение в точках -сети. , . Необходимо, чтобы - в этом случае говорим, что объект -управляем и при этом . Отсюда имеем следующее . Если , то -объект E-управляем. Если -объект не управляем. Если , то в этом случае неопределенность. Выясним вопрос о погрешности.и -погрешность для вычисления опорной функций и .- погрешность для вычисления . По условию Липшица ,

. Используем эти формулы , получим следующие погрешности: - погрешность для вычисления -предполагается, что она интегрируема по Лебегу. -это вычисление интеграла . - погрешность для вычисления . -погрешность вычисления минимума функций. , . +++++++

Похожие работы

Достаточно общая теория управления (Расовые доктрины в России: их возможности и целесообразность следования им в исторической перспективе)

Скачать

795696

13

12

... за собой её гибель, либо требующие подключения к процессу самоуправления суперсистемы иерархически высшего управления. Так соборный интеллект видится индивидуальному интеллекту с точки зрения достаточно общей теории управления; возможно, что кому-то всё это, высказанное о соборных интеллектах, представляется бредом, но обратитесь тогда к любому специалисту по вычислительной технике: примитивная ...

Теория управления фирмой

Скачать

65851

0

2

... важности человеческого фактора; использовании интеллектуального потенциала; преобладании психологических социальных факторов и групповых норм поведения. Начиная с 70-х годов, стала развиваться ситуационная теория управления. Ее главной особенностью является стремление к достижению согласованности между организационной и поведенческой сторонами управления в зависимости от характера производства и ...

Что мешает вам освоить теорию управления (и для чего вам это нужно)

Скачать

14050

0

0

... эффективность инвестиций в рекламу? Желая получить ответ на возникший вопрос, руководитель попадает в одну из двух ловушек: утверждается в бесполезности теории управления для решения его практической задачи; находит простое и, естественно, неправильное решение, после чего либо попадает в первую ловушку, либо продолжает поиск волшебных таблеток. Кроме того, многие руководители не хотят ...

Теория управления и империя игр в системе социального управления

Скачать

43837

0

0

... профессиональных предписания); по последствиям реализации того или иного типа поведения для группы (социальной системы) - конструктивное и деструктивное; по форме протекания - кооперированное (ориентированное на поддержание сотрудничества) и конфликтное. В настоящее время в теории управления организационное поведение является одной из наиболее активно развивающейся отраслей управленческой науки, ...