Навигация
ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
1.4. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ.
Второе начало термодинамики устанавливает наличие в природе фундаментальной асимметрии , т.е. однонаправленности всех происходящих в ней самопроизвольных процессов .
Второй основной постулат термодинамики связан так же с другими свойствами термодинамического равновесия как особого вида теплового движения. Опыт показывает , что если две равновесные системы А и В привести в тепловой контакт , то независимо от различия или равенства у них внешних параметров они или остаются по прежнему в состоянии термодинамического равновесия , или равновесие у них нарушается и спустя некоторое время в процессе теплообмена ( обмена энергией ) обе системы приходят в другое равновесное состояние. Кроме того , если имеются три равновесные системы А,В и С и если системы А и В поразнь находятся в равновесии с системой С, то системы А и В находятся в термодинамическом равновесии и между собой (свойства транзитивности термодинамического равновесия ).
Пусть имеются две системы . Для того , чтобы убедится в том , что они находятся в состоянии термодинамического равновесия надо измерить независимо все внутренние параметры этих систем и убедиться в том , что они постоянны во времени. Эта задача черезвычайно трудная .
Оказывается однако , что имеется такая физическая величина , которая позволяет сравнить термодинамические состояния двух систем и двух частей одной системы без подробного исследования и внутренних параметров. Эта величина , выражающая состояние внутреннего движения равновесной системы , имеющая одно и то же значение у всех частей сложной равновесной системы независимо от числа частиц в них и определяемое внешними параметрами и энергией называется температурой .
Температура является интенсивным параметром и служит мерой интенсивности теплового движения молекул.
Изложенное положение о существовании температуры как особой функции состояния равновесной системы представляет второй постулат термодинамики.
Иначе говоря , состояние термодинамического равновесия определяется совокупностью внешних параметров и температуры.
Р.Фаулер и Э.Гуггенгейм назвали его нулевым началом , так как оно подобно первому и второму началу определяющим существование некоторых функций состояния , устанавливает существование температуры у равновесных систем. Об этом упоминалось выше.
Итак , все внутренние параметры равновесной системы являются функциями внешних параметров и температур .(Второй постулат термодинамики).
Выражая температуру через внешние параметры и энергию , второй постулат можно сформулировать в таком виде : при термодинамическом равновесии все внутренние параметры являются функциями внешних параметров и энергии.
Второй постулат позволяет определить изменение температуры тела по изменению какого либо его параметра , на чем основано устройство различных термометров.
1.4.1. ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ.
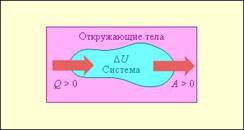
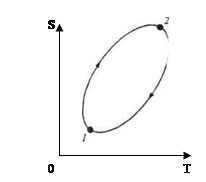
Процесс перехода системы из состояния 1 в 2 называется обратимым , если возвращением этой системы в исходное состояние из 2 в 1 можно осуществить без каких бы то ни было изменений окружающих внешних телах.
Процесс же перехода системы из состояния 1 в 2 называется необратимым , если обратный переход системы из 2 в 1 нельзя осуществить без изменения в окружающих телах .
Мерой необратимости процесса в замкнутой системе является изменением новой функции состояния - энтропии , существование которой у равновесной системы устанавливает первое положение второго начала о невозможности вечного двигателя второго рода . Однозначность этой функции состояния приводит к тому , что всякий необратимый процесс является неравновесным.
Из второго начала следует , что S является однозначной функцией состояния. Это означает , что dQ/T для любого кругового равновесного процесса равен нулю. Если бы это не выполнялось , т.е. если бы энтропия была неоднозначной функцией состояния то , можно было бы осуществить вечный двигатель второго рода.
Положение о существовании у всякой термодинамической системы новой однозначной функцией состояния энтропии S , которая при адиабатных равновесных процессах не изменяется и состовляет содержание второго начала термодинамики для равновесных процессов.
Математически второе начало термодинамики для равновесных процессов записывается уравнением:
dQ/T = dS или dQ = TdS (1.3)
Интегральным уравнением второго начала для равновесных круговых процессов является равенство Клаузиуса :
dQ/T = 0 (1.4)
Для неравновесного кругового процесса неравенство Клаузиуса имеет следующий вид :
dQ/T < 0 (1.5)
Теперь можно записать основное уравнение термодинамики для простейшей системы находящейся под всесторонним давлением :
TdS = dU + pdV (1.6)
Обсудим вопрос о физическом смысле энтропии.
Похожие работы
... и химическим процессам, происходящим в веществе, в различных системах. Важным достижением на пути этого процесса интеграции знаний было открытие фундаментального закона природы - закона сохранения и превращения энергии. Основатель термодинамики С. Карно в своем труде "Размышления о движущей силе огня и о машинах, способах развивать эту силу" пишет: "Тепло - это не что иное, как движущая сила, ...
... , или термодинамическое равновесие, при котором движение частиц хаотично. Максимальная энтропия означает полное термодинамическое равновесие, что эквивалентно хаосу. Часто второе начало термодинамики преподносится как объединенный принцип существования и возрастания энтропии. Принцип существования энтропии формулируется как математическое выражение энтропии термодинамических систем в условиях ...
... , не вызывая при этом никаких других изменений состояния системы. (Такую воображаемую машину принято называть вечным двигателем второго рода) 6. Обратимые и необратимые процессы По второму началу термодинамики в природе возможны процессы, при которых превращение теплоты в работу связано с компенсацией, и невозможны процессы, при которых такое превращение не сопровождается компенсацией. Это ...
... эффекта термодинамического процесса (2.5). Запишем: . (2.16) Выражение (2.16) и подобные ему, некоторые авторы называют обобщенной формулировкой I и II начала термодинамики. Преобразуем дифференциал , и подставим его в (2.5): . Из последнего равенства следует: , , . (2.17) Учитывая, что ...
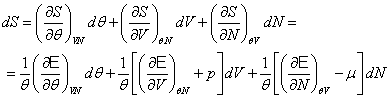
0 комментариев