Навигация
3.3. ДИНАМИКА ПОПУЛЯЦИИ .
О распространении и численности видов была собрана обширная информация . Макроскопической характеристикой , описывающей популяцию , может быть число особей в популяции . Это число играет роль параметра порядка . Если различные виды поддерживаются общим пищевым ресурсом , то начинается межвидовая борьба , и тогда применим принцип Дарвина : выживает наиболее приспособленный вид . ( Нельзя не отметить сильнейшую аналогию , существующую между конкуренцией лазерных мод и межвидовой борьбой ). Если имеются однотипные пищевые ресурсы , то становится возможным сосуществование видов . Численность видов может быть подвержена временным колебаниям.
ОДИН ВИД.
Рассмотрим сначала одну популяцию с числом особей в ней n . При наличии пищевых ресурсов А особи размножаются со скоростью :
и гибнут со скоростью :
Здесь k и d - некоторые коэффициенты рождаемости и смертности , в общем случае зависящее от параметров внешней среды обитания . Если бы количество пищи было неограниченно , то эволюционное уравнение выглядело бы так :
Введем обозначение a = kA - d
Оно было бы линейным и описывало бы неограниченный экспериментальный рост (при kA > d), либо экспериментальную гибель (при kA < d) популяции.
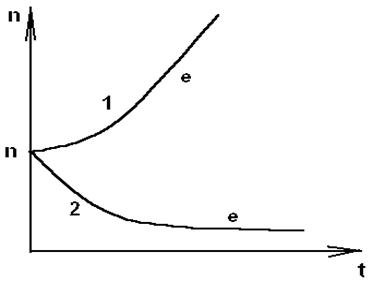
Рис. 3.4 Кривая 1: Экспоненциальный рост ; a>0 , kA>d
Кривая 2: Экспоненциальная гибель ; a>0 , kA>d.
|
|
В общем случае , однако , пищевые ресурсы ограничены , так что скорость потребления пищи
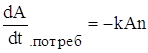
Вместе с тем в общем случае возможно восстановление пищевых ресурсов со скоростью :
Здесь , конечно , рассмотрен придельный случай сохранения полного количества органического вещества
A + n = N = const ,
N - способность среды обитания поддерживать популяцию.
Тогда с учетом A = N - n получится следующее уравнение эволюции популяции одного вида (логистическое уравнение Ферхюльста ) :
(3.17)
Решим уравнение (3.17) аналитически , перепишем его следующим образом
, обозначим kN - d = k1
Получим :
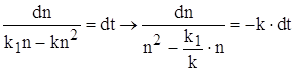
Воспользуемся 
табличным интегралом ,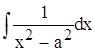 
,полученное уравнение примет вид :
решим это уравнение , преобразуя
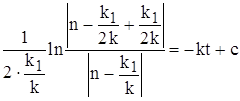
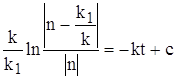
сократим полученное выражение на k , и перенесем переменную k1 в правую часть , получим
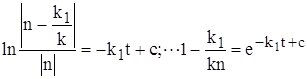
отсюда n(t) ® 
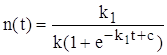
Начальные условия :
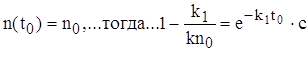
откуда
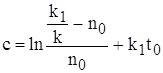
Подставляя с в решение , получим уравнение в следующем виде
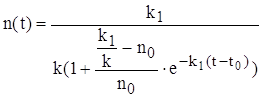
ранее мы обозначали , что 
, подставляем и преобразуем
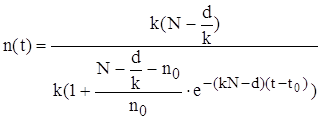
сократим на k - коэффициент рождаемости , окончательно получим решение уравнения (3.17)
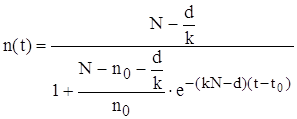
Итак , получено аналитическое решение логистического уравнения - это решение указывает на то , что рост популяции останавливается на некотором конечном стационарном уровне:
то есть параметр n1 указывает высоту плато насыщения , к которому стремится n(t) с течением времени .
Параметр n0 указывает начальное значение численности одного вида популяции : n0 = n(t0) . Действительно , 
,то есть n1 - предельная численность вида в данной среде обитания . Иначе говоря , параметр n1 характеризует емкость среды по отношению к данной популяции . И наконец , параметр (kN - d) задает крутизну начального роста .
Отметим , что при малой исходной численности n0 (начальное число особи) начальный рост популяций будет почти экспоненциальным
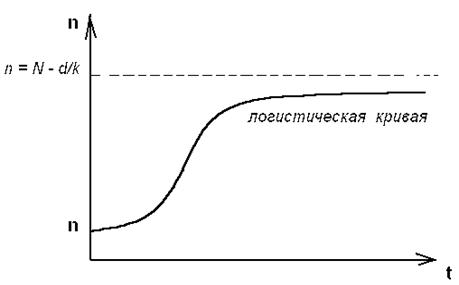
Рис. 3.5. Логистическая кривая.
(эволюция популяции одного вида)
Решение уравнения (3.17) можно представить с помощью логистической кривой (рис. 3.5) . Эволюция полностью детерминирована . Популяция перестает расти , когда ресурс среды оказывается исчерпанным .
Самоорганизация - при ограниченном пищевом ресурсе. Система самоорганизованна и взрывоподобный рост популяции (рис. 3.4 Кривая 1) сменяется кривой с насыщением .
Подчеркнем , что при описании данной биологической системы используют понятийный и физико-математический аппарат из нелинейной неравновесной термодинамики.
Может случится , однако, что всегда за событиями , не управляемыми в рамках модели , в той же среде появится , первоначально в малых количествах , новые виды (характеризуемые другими экологическими параметрами k,N и d) . В связи с такой экологической флуктуацией возникает вопрос о структурной устойчивости : новые виды могут либо исчезнуть , либо вытеснить первоначальных обитателей . Пользуясь линейным анализом устойчивости , не трудно показать , что новые виды вытесняют старые только в том случае , если
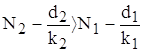
Последовательность , в которой виды заполняют экологическую нишу , представлена на рисунке 3.6.
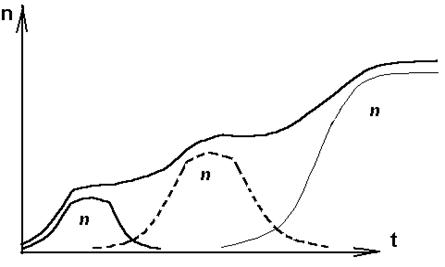
Рис. 3.6. Последовательное заполнение экологической
ниши различными видами .
Эта модель позволяет придать точным количественный смысл утверждению о том , что «выживает наиболее приспособленный» , в рамках задачи о заполнении заданной экологической ниши .
Похожие работы
... и химическим процессам, происходящим в веществе, в различных системах. Важным достижением на пути этого процесса интеграции знаний было открытие фундаментального закона природы - закона сохранения и превращения энергии. Основатель термодинамики С. Карно в своем труде "Размышления о движущей силе огня и о машинах, способах развивать эту силу" пишет: "Тепло - это не что иное, как движущая сила, ...
... , или термодинамическое равновесие, при котором движение частиц хаотично. Максимальная энтропия означает полное термодинамическое равновесие, что эквивалентно хаосу. Часто второе начало термодинамики преподносится как объединенный принцип существования и возрастания энтропии. Принцип существования энтропии формулируется как математическое выражение энтропии термодинамических систем в условиях ...
... , не вызывая при этом никаких других изменений состояния системы. (Такую воображаемую машину принято называть вечным двигателем второго рода) 6. Обратимые и необратимые процессы По второму началу термодинамики в природе возможны процессы, при которых превращение теплоты в работу связано с компенсацией, и невозможны процессы, при которых такое превращение не сопровождается компенсацией. Это ...
... эффекта термодинамического процесса (2.5). Запишем: . (2.16) Выражение (2.16) и подобные ему, некоторые авторы называют обобщенной формулировкой I и II начала термодинамики. Преобразуем дифференциал , и подставим его в (2.5): . Из последнего равенства следует: , , . (2.17) Учитывая, что ...
0 комментариев