Навигация
ОБЩАЯ ХАРАКТЕРИСТИКА ОТКРЫТЫХ СИСТЕМ
2.1. ОБЩАЯ ХАРАКТЕРИСТИКА ОТКРЫТЫХ СИСТЕМ.
Открытые системы - это термодинамические системы , которые обмениваются с окружающими телами ( средой ) , веществом , энергией и импульсом . Если отклонение открытой системы от состояния равновесия невелико , то неравновесное состояние можно описать теми же параметрами (температура , химический потенциал и другие) , что и равновесное . Однако отклонение параметров от равновесных значений вызывают потоки вещества и энергии в системе . Такие процессы переноса приводят к производству энтропии . Примерами открытых систем являются : биологические системы , включая клетку , системы обработки информации в кибернетике , системы энергоснабжения и другие . Для поддержания жизни в системах от клетки до человека необходим постоянный обмен энергией и веществом с окружающей средой . Следовательно живые организмы являются системами открытыми , аналогично и с другими приведенными параметрами. Пригожиным в 1945 году был сформулирован расширенный вариант термодинамики.
В открытой системе изменение энтропии можно разбить на сумму двух вкладов :
d S = d Se + d Si (2.1)
Здесь d Se - поток энтропии , обусловленный обменом энергией и веществом с окружающей средой , d Si - производство энтропии внутри системы (рис. 2.1).
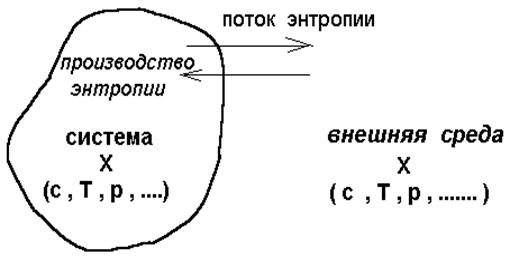
Рис. 2.1. Схематическое представление открытых
систем : производство и поток энтропии.
Х - набор характеристик :
С - состав системы и внешней среды ;
Р - давление ; Т - температура.
Итак , открытая система отличается от изолированной наличием члена в выражении для изменения энтропии , соответствующего обмену . При этом знак члена d Se может быть любым в отличии от d Si .
Для неравновесного состояния :
S < Smax
Неравновесное состояние более высокоорганизованно , чем равновесное , для которого
S = Smax
Таким образом эволюцию к более высокому порядку можно представить как процесс , в котором система достигает состояния с более низкой энтропией по сравнению с начальной .
Фундаментальная теорема о производстве энтропии в открытой системе с независимыми от времени краевыми условиями была сформулирована Пригожиным: в линейной области система эволюционирует к стационарному состоянию , характеризуемому минимальным производством энтропии , совместимым с наложенными граничными условиями .
Итак состояние всякой линейной открытой системы с независящими от времени краевыми условиями всегда изменяется в направлении уменьшения производства энтропии P = d S / d t пока не будет достигнуто состояние текущего равновесия , при котором производство энтропии минимально :
d P < 0 (условие эволюции)
P = min , d P = 0 (условие текущего равновесия)
d P/ d t < 0 (2.2)
2.1.1. ДИССИПАТИВНЫЕ СТРУКТУРЫ.
Каждая система состоит из элементов (подсистем) . Эти элементы находятся в определенном порядке и связаны определенными отношениями. Структуру системы можно назвать организацию элементов и характер связи между ними.
В реальных физических системах имеются пространственные и временные структуры .
Формирование структуры - это возникновение новых свойств и отношений в множестве элементов системы . В процессах формирования структур играют важную роль понятия и принципы :
1. Постоянный отрицательный поток энтропии .
2. Состояние системы в дали от равновесия .
3. Нелинейность уравнений описывающих процессы .
4. Коллективное (кооперативное) поведение подсистем .
5. Универсальный критерий эволюции Пригожина - Гленсдорфа.
Формирование структур при необратимых процессах должно сопровождаться качественным скачком (фазовым переходом) при достижении в системе критических значений параметров. В открытых системах внешний вклад в энтропию (2.1) d S в принципе можно выбрать произвольно , изменяя соответствующим образом параметры системы и свойства окружающей среды . В частности энтропия может уменьшаться за счет отдачи энтропии во внешнюю среду , т.е. когда d S < 0 . Это может происходить , если изъятие из системы в единицу времени превышает производство энтропии внутри системы , то есть
d S dSe dSi
¾ < 0 , если ¾ > ¾ > 0 (2.3)
d t dt dt
Чтобы начать формирование структуры , отдача энтропии должна превысить некоторое критическое значение . В сильно неравновесном расстоянии переменные системы удовлетворяют нелинейным уравнениям .
Таким образом , можно выделить два основных класса необратимых процессов :
1. Уничтожение структуры вблизи положения равновесия . Это универсальное свойство систем при произвольных условиях .
2. Рождение структуры вдали от равновесия в открытой системе при особых критических внешних условиях и при нелинейной внутренней динамики . Это свойство не универсально .
Пространственные , временные или пространственно-временные структуры , которые могут возникать вдали от равновесия в нелинейной области при критических значениях параметров системы называются диссипативными структурами.
В этих структурах взаимосвязаны три аспекта :
1. Функция состояния , выражаемая уравнениями .
2. Пространственно - временная структура , возникающая из-за неустойчивости .
3. Флуктуации , ответственные за неустойчивости .![]()
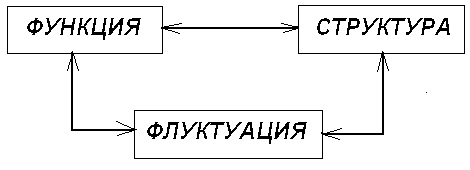
Рис. 1. Три аспекта диссипативных структур.
Взаимодействия между этими аспектами приводит к неожиданным явлениям - к возникновению порядка через флуктуации , формированию высокоорганизованной структуры из хаоса.
Таким образом , в диссипативных структурах происходит становление из бытия , формируется возникающее из существующего.
Похожие работы
... и химическим процессам, происходящим в веществе, в различных системах. Важным достижением на пути этого процесса интеграции знаний было открытие фундаментального закона природы - закона сохранения и превращения энергии. Основатель термодинамики С. Карно в своем труде "Размышления о движущей силе огня и о машинах, способах развивать эту силу" пишет: "Тепло - это не что иное, как движущая сила, ...
... , или термодинамическое равновесие, при котором движение частиц хаотично. Максимальная энтропия означает полное термодинамическое равновесие, что эквивалентно хаосу. Часто второе начало термодинамики преподносится как объединенный принцип существования и возрастания энтропии. Принцип существования энтропии формулируется как математическое выражение энтропии термодинамических систем в условиях ...
... , не вызывая при этом никаких других изменений состояния системы. (Такую воображаемую машину принято называть вечным двигателем второго рода) 6. Обратимые и необратимые процессы По второму началу термодинамики в природе возможны процессы, при которых превращение теплоты в работу связано с компенсацией, и невозможны процессы, при которых такое превращение не сопровождается компенсацией. Это ...
... эффекта термодинамического процесса (2.5). Запишем: . (2.16) Выражение (2.16) и подобные ему, некоторые авторы называют обобщенной формулировкой I и II начала термодинамики. Преобразуем дифференциал , и подставим его в (2.5): . Из последнего равенства следует: , , . (2.17) Учитывая, что ...
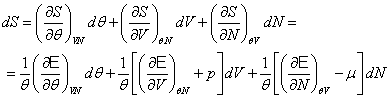
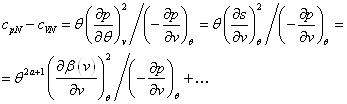
0 комментариев