Навигация
ПРИМЕРЫ САМООРГАНИЗАЦИИ РАЗЛИЧНЫХ
2.3 ПРИМЕРЫ САМООРГАНИЗАЦИИ РАЗЛИЧНЫХ
СИСТЕМ.
Рассмотрим в качестве иллюстрации некоторые примеры самоорганизации систем в физике , химии , биологии и социуме.
2.3.1. ФИЗИЧЕСКИЕ СИСТЕМЫ.
В принципе даже в термодинамическом равновесии можно указать примеры самоорганизации , как результаты коллективного поведения . Это , например , все фазовые переходы в физических системах , такие как переход жидкость - газ , ферромагнитный переход или возникновение сверхпроводимости . В неравновесном состоянии можно назвать примеры высокой организации в гидродинамике , в лазерах различных типов , в физике твердого тела - осциллятор Ганна , туннельные диоды , рост кристаллов .
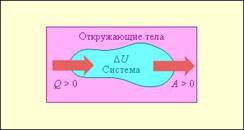
В открытых системах , меняя поток вещества и энергии из вне , можно контролировать процессы и направлять эволюцию систем к состояниям , все более далеким от равновесия . В ходе неравновесных процессов при некотором критическом значении внешнего потока из неупорядоченных и хаотических состояний за счет потери их устойчивости могут возникать упорядоченные состояния , создаваться диссипативные структуры .
2.3.1а. ЯЧЕЙКИ БЕНАРА.
Классическим примером возникновения структуры из полностью хаотической фазы являются конвективные ячейки Бенара . В 1900 году была опубликована статья Х.Бенара с фотографией структуры , по виду напоминавшей пчелиные соты (рис. 2.7).
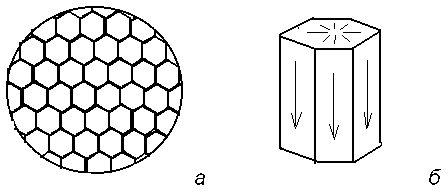
Рис. 2.7. Ячейки Бенара :
а) - общий вид структуры
б) - отдельная ячейка.
Эта структура образовалась в ртути , налитой в плоский широкий сосуд , подогреваемый снизу , после того как температурный градиент превысил некоторое критическое значение . Весь слой ртути (или другой вязкой жидкости) распадался на одинаковые вертикальные шестигранные призмы с определенным соотношением между стороной и высотой (ячейки Бенара). В центральной области призмы жидкость поднимается , а вблизи вертикальных граней - опускается . Возникает разность температур Т между нижней и верхней поверхностью DТ = Т2 - Т1 > 0 .Для малых до критических разностей DТ < DТkp жидкость остается в покое , тепло снизу вверх передается путем теплопроводности . При достижении температуры подогрева критического значения Т2 = Тkp (соответственно DТ = DТkp ) начинается конвекция . При достижении критического значения параметра Т , рождается , таким образом , пространственная диссипативная структура . При равновесии температуры равны Т2 =Т1 , DТ = 0 . При кратковременном подогреве (подводе тепла) нижней плоскости , то есть при кратковременном внешнем возмущении температура быстро станет однородной и равной ее первоначальному значению . Возмущение затухает , а состояние - асимптотически устойчиво. При длительном , но до критическом подогреве ( DТ < DТkp ) в системе снова установится простое и единственное состояние , в котором происходит перенос к верхней поверхности и передачи его во внешнюю среду (теплопроводность) , рис. 2.8 , участок а . Отличие этого состояния от равновесного состояния состоит в том , что температура , плотность , давление станут неоднородными . Они будут приблизительно линейно изменяться от теплой области к холодной .
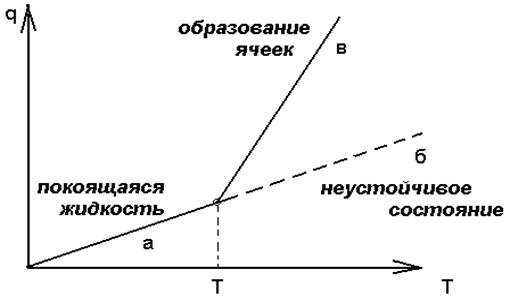
Рис. 2.8. Поток тепла в тонком слое жидкости.
Увеличение разности температур DТ , то есть дальнейшее отклонение системы от равновесия , приводит к тому , что состояние неподвижной теплопроводящей жидкости становится неустойчивым участок б на рисунке 2.8. Это состояние сменяется устойчивым состоянием (участок в на рис. 2.8) , характеризующимся образованием ячеек . При больших разностях температур покоящаяся жидкость не обеспечивает большой перенос тепла , жидкость ²вынуждена² двигаться , причем кооперативным коллективным согласованном образом.
Далее этот вопрос рассматривается в 3 главе.
2.3.1в. ЛАЗЕР , КАК САМООРГАНИЗУЮЩАЯСЯ
СИСТЕМА.
Итак , в качестве примера физической системы , упорядоченность которой есть следствие внешнего воздействия , рассмотрим лазер.
При самом грубом описании лазер - это некая стеклянная трубка , в которую поступает свет от некогерентного источника (обычной лампы) , а выходит из нее узконаправленный когерентный световой пучок , при этом выделяется некоторое количества тепла.
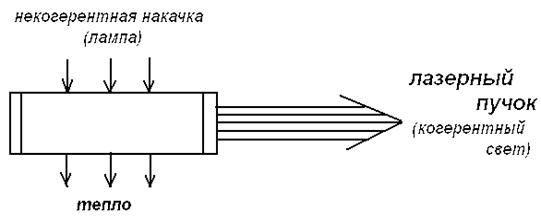
При малой мощности накачки эти электромагнитные волны , которые испускает лазер , некоррелированные , и излучение подобно излучению обычной лампы. Такое некогерентное излучение - это шум , хаос. При повышении внешнего воздействия в виде накачки до порогового критического значения некогерентный шум преобразуется в ²чистый тон² , то есть испускает число синусоидальная волна - отдельные атомы ведут себя строго коррелированным образом , самоорганизуются.
Лампа ® Лазер
Хаос ® Порядок
Шум ® Когерентное излучение
В сверхкритической области режим ²обычной лампы² оказывается не стабильным , а лазерный режим стабильным , рисунок 2.9.
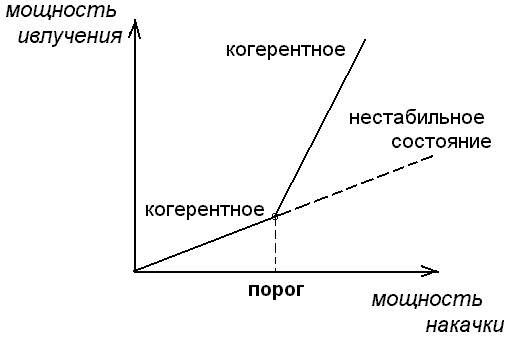
Рис. 2.9. Излучение лазера в до критической (а) и
сверхкритической (б) области.
Видно , что образование структуры в жидкости и в лазере формально описывается весьма сходным образом . Аналогия связана с наличием тех же самых типов бифуркаций в соответствующих динамических уровнях.
Подробнее этот вопрос рассмотрим в практической части , в 3 главе.
Похожие работы
... и химическим процессам, происходящим в веществе, в различных системах. Важным достижением на пути этого процесса интеграции знаний было открытие фундаментального закона природы - закона сохранения и превращения энергии. Основатель термодинамики С. Карно в своем труде "Размышления о движущей силе огня и о машинах, способах развивать эту силу" пишет: "Тепло - это не что иное, как движущая сила, ...
... , или термодинамическое равновесие, при котором движение частиц хаотично. Максимальная энтропия означает полное термодинамическое равновесие, что эквивалентно хаосу. Часто второе начало термодинамики преподносится как объединенный принцип существования и возрастания энтропии. Принцип существования энтропии формулируется как математическое выражение энтропии термодинамических систем в условиях ...
... , не вызывая при этом никаких других изменений состояния системы. (Такую воображаемую машину принято называть вечным двигателем второго рода) 6. Обратимые и необратимые процессы По второму началу термодинамики в природе возможны процессы, при которых превращение теплоты в работу связано с компенсацией, и невозможны процессы, при которых такое превращение не сопровождается компенсацией. Это ...
... эффекта термодинамического процесса (2.5). Запишем: . (2.16) Выражение (2.16) и подобные ему, некоторые авторы называют обобщенной формулировкой I и II начала термодинамики. Преобразуем дифференциал , и подставим его в (2.5): . Из последнего равенства следует: , , . (2.17) Учитывая, что ...
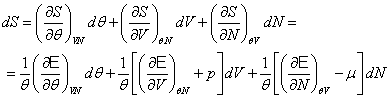
0 комментариев