Навигация
3.1. ЯЧЕЙКИ БЕНАРА .
Для того , чтобы экспериментально изучить структуры , достаточно иметь сковороду , немного масла и какой ни будь мелкий порошок , чтобы было заметно движение жидкости . Нальем в сковороду масло с размешанным в нем порошком и будем подогревать ее снизу (рис. 3.1)
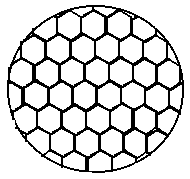
Рис. 3.1. Конвективные ячейки Бенара.
Если дно сковороды плоское и нагреваем мы ее равномерно , то можно считать , что у дна и на поверхности поддерживаются постоянные температуры , снизу - Т1 , сверху - Т2 . Пока разность температуры DТ = Т1 - Т2 невелика , частички порошка неподвижны , а следовательно , неподвижна и жидкость .
Будем плавно увеличивать температуру Т1 . С ростом разности температур до значения DТc наблюдается все та же картина , но когда DТ > DТc , вся среда разбивается на правильные шестигранные ячейки (см. Рис. 3.1) в центре каждой из которых жидкость движется вверх , по кроям вниз . Если взять другую сковороду , то можно убедиться , что величина возникающих ячеек практически не зависит от ее формы и размеров . Этот замечательный опыт впервые был проделан Бенаром в начале нашего века , а сами ячейки получили название ячеек Бенара .
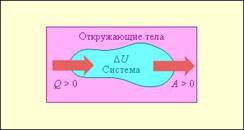
Элементарное качественное объяснения причины движения жидкости заключается в следующем . Из-за теплового расширения жидкость расслаивается , и в более нижнем слое плотность жидкости r1 меньше , чем в верхнем r2 . Возникает инверсный градиент плотности , направленный противоположно силе тяжести . Если выделить элементарный объем V , который немного смещается вверх в следствии возмущения , то в соседнем слое архимедова сила станет больше силы тяжести , так как r2 > r1 . В верхней части малый объем , смещаясь вниз , поподает в облость пониженной плотности , и архимедова сила будет меньше силы тяжести FA < FT , возникает нисходящее движение жидкости . Направление движения нисходящего и восходящего потоков в данной ячейке случайно , движение же потоков в соседних ячейках , после выбора направлений в данной ячейке детерминировано . Полный поток энтропии через границы системы отрицателен , то есть система отдает энтропию , причем в стационарном состоянии отдает столько , сколько энтропии производится внутри системы (за счет потерь на трение).
dSe q q T1 - T2
¾ = ¾ - ¾ = q * ¾¾¾ < 0 (3.1)
dt T2 T1 T1 * T2
Образование именно сотовой ячеистой структуры объясняется минимальными затратами энергии в системе на создание именно такой формы пространственной структуры . При этом в центральной части ячейки жидкость движется вверх , а на ее периферии - вниз.
Дальнейшее сверхкритическое нагревание жидкости приводит к разрушению пространственной структуры - возникает хаотический турбулентный режим.
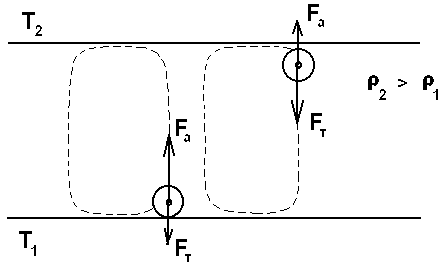
Рис. 3.2. Иллюстрация возникновения тепловой
конвекции в жидкости .
К этому вопросу прикладывается наглядная иллюстрация возникновения тепловой конвекции в жидкости .
3.2 ЛАЗЕР , КАК САМООРГАНИЗУЮЩАЯСЯ СИСТЕМА.
Во второй главе этот вопрос мы уже рассматривали . Здесь же , рассмотрим простую модель лазера .
Лазер - это устройство , в котором в процессе стимулированного излучения порождаются фотоны .
Изменение со временем числа фотонов n , или другими словами , скорость порождения фотонов , определяется уравнением вида :
dn / dt = «Прирост» - «Потери» (3.2)
Прирост обусловлен так называемым стимулированном излучением . Он пропорционален числу уже имеющихся фотонов и числу возбужденных атомов N . Таким образом :
Прирост = G N n (3.3)
Здесь G - коэффициент усиления , который может быть получен из микроскопической теории . Член , описывающий потери , обусловлен уходом фотонов через торцы лазера . Единственное допущение , которое мы принимаем , - это то , что скорость ухода пропорциональна числу имеющихся фотонов . Следовательно ,
Потери = 2cn (3.4)
2c = 1/ t0 , где t0 - время жизни фотона в лазере .
Теперь следует учесть одно важное обстоятельство , которое делает (2.1) нелинейным уравнением вида :
(3.5)
Число возбужденных атомов уменьшается за счет испускания фотонов . Это уменьшение DN пропорционально числу имеющихся в лазере фотонов , поскольку эти фотоны постоянно заставляют атомы возвращаться в основное состояние .
DN = an (3.6)
Таким образом , число возбужденных атомов равно
N = N0 - DN (3.7)
где N0 - число возбужденных атомов , поддерживаемое внешней
накачкой , в отсутствии лазерной генерации.
Подставляя (3.3) - (3.7) в (3.2) , получаем основное уравнение нашей упрощенной лазерной модели :
(3.8)
где постоянная k дает выражение :
k1 = aG
k = 2c - GN0 >< 0 (3.9)
Если число возбужденных атомов N0 (создаваемых накачкой) невелико , то k положительно , в то время как при достаточно больших N0 k - может стать отрицательным . Изменение знака происходит когда
GN0 = 2c (3.10)
Это условие есть условие порога лазерной генерации .
Из теории бифуркации следует , что при k > 0 лазерной генерации нет , в то время как при k < 0 лазер испускает фотоны.
Ниже или выше порога лазер работает в совершено разных режимах .
Решим уравнение (3.8) и проанализируем его аналитически :
- это уравнение одномодового лазера .
Запишем уравнение (3.8) в следующем виде :
Разделим исходное уравнение на n2 .
и введем новую функцию Z :
1/n = n-1 = Z Þ Z1 = - n-2 следовательно уравнение примет вид :
перепишем его в следующем виде :
разделим обе части данного уравнения на -1 , получим
(3.11)
Уравнение (3.11) - это уравнение Бернулли , поэтому сделаем следующую замену Z = U×V , где U и V неизвестные пока функции n , тогда Z1 = U1 V + U V1 .
Уравнение (3.11) , после замены переменных , принимает вид
U1 V + UV1 - k UV = k1
преобразуем , получим
U1 V + U(V1 - k V) = k1 (3.12)
Решим уравнение (3.12)
V1 - k V = 0 ® dV/dt = k V
сделаем разделение переменных dV/V =k dt ® ln V = k t
результат V = ekt (3.13)
Отсюда мы можем уравнение (3.12) переписать в виде :
U1 ekt = k1
- это то же самое , что dU/dt = k1e-kt , dU = k1e -kt dt выразим отсюда U , получим
(3.14)
По уравнению Бернулли мы делали замену Z = U V подставляя уравнения (3.13) и (3.14) в эту замену , получим
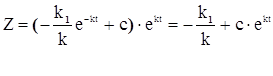
Ранее вводили функцию Z = n-1 , следовательно
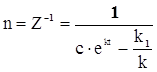(3.15)
Начальное условие n0=1/(c-k1/k) , из этого условия мы можем определить константу с следующим образом
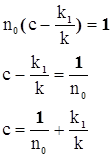
Подставляя , найденную нами константу в уравнение (3.15) , получим
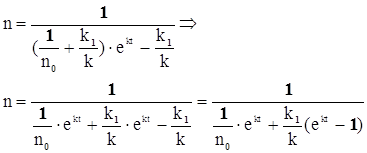(3.16)
Исследуем функцию (3.16) при k = 0 , k < 0 , k > 0 .
При k®0 ; ekt ® 0 ; (ekt - 1)®0 , то есть (ekt - 1)×k1/k®0×¥ (неопределенность) , раскроем эту неопределенность по правилу Лопиталя . Эту неопределенность вида 0×¥ следует привести к виду 
. При этом , как и всегда при применении правила Лопиталя , по ходу вычислений рекомендуется упрощать получившиеся выражения , следующим образом :
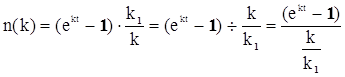
n(k)при k®0 ® 0 , следовательно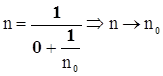 
Перепишем (3.16) в следующем виде
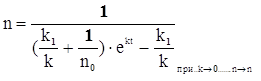
Линеаризуем нелинейное уравнение , получим
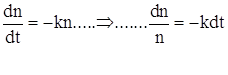
ln n = - kt + c Þ 
Построим график для этих условий
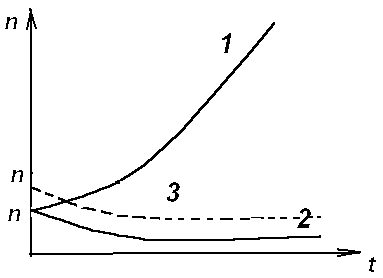
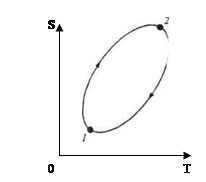
Рис. 3.3 К самоорганизации в одномодовом лазере :
кривая 1 : k < 0 , режим лазерной генерации
кривая 2 : k = 0 , точка бифуркации , порог
кривая 3 : k > 0 , режим лампы.
При k = 0 уравнение (3.8) примет вид
решая его , получим
(3.8)
При условии 
; n(t) = const , функция (3.8) приближается к стационарному состоянию , не зависимо от начального значения n0 , но в зависимости от знаков k и k1 (смотри рисунок 3.3).
Таким образом , функция (3.8) принимает стационарное решение
Похожие работы
... и химическим процессам, происходящим в веществе, в различных системах. Важным достижением на пути этого процесса интеграции знаний было открытие фундаментального закона природы - закона сохранения и превращения энергии. Основатель термодинамики С. Карно в своем труде "Размышления о движущей силе огня и о машинах, способах развивать эту силу" пишет: "Тепло - это не что иное, как движущая сила, ...
... , или термодинамическое равновесие, при котором движение частиц хаотично. Максимальная энтропия означает полное термодинамическое равновесие, что эквивалентно хаосу. Часто второе начало термодинамики преподносится как объединенный принцип существования и возрастания энтропии. Принцип существования энтропии формулируется как математическое выражение энтропии термодинамических систем в условиях ...
... , не вызывая при этом никаких других изменений состояния системы. (Такую воображаемую машину принято называть вечным двигателем второго рода) 6. Обратимые и необратимые процессы По второму началу термодинамики в природе возможны процессы, при которых превращение теплоты в работу связано с компенсацией, и невозможны процессы, при которых такое превращение не сопровождается компенсацией. Это ...
... эффекта термодинамического процесса (2.5). Запишем: . (2.16) Выражение (2.16) и подобные ему, некоторые авторы называют обобщенной формулировкой I и II начала термодинамики. Преобразуем дифференциал , и подставим его в (2.5): . Из последнего равенства следует: , , . (2.17) Учитывая, что ...
0 комментариев