Навигация
2.3.2. ХИМИЧЕСКИЕ СИСТЕМЫ .
В этой области синергетика сосредотачивает свое внимание на тех явлениях , которые сопровождаются образованием макроскопических структур . Обычно если дать реагентам про взаимодействовать, интенсивно перемешивая реакционную смесь, то конечный продукт получается однородный . Но в некоторых реакциях могут возникать временные, пространственные или смешанные ( пространственные - временные) структуры . Наиболее известным примером может служить реакция Белоусова - Жаботинского .
2.3.2а. РЕАКЦИЯ БЕЛАУСОВА - ЖАБОТИНСКОГО.
Рассмотрим реакцию Белоусова -Жаботинского . В колбу сливают в определенных пропорциях Ce2(SO4) , KBrO3 , CH2(COOH)2, H2SO4 , добавляют несколько капель индикатора окисления - восстановления - ферроина и перемешивают . Более конкретно - исследуются окислительно - восстановительные реакции
Ce 3+_ _ _ Ce 4+ ; Ce 4+_ _ _ Ce 3+
в растворе сульфата церия , бромида калия , малоковой кислоты и серной кислоты . Добавление феррогена позволяет следить за ходом реакции по изменению цвета ( по спектральному поглащению ) . При высокой концентрации реагирующих веществ , превышающих критическое значение сродства , наблюдаются необычные явления .
При составе
сульфат церия - 0,12 ммоль/л
бромида калия - 0,60 ммоль/л
малоковой кислоты - 48 ммоль/л
3-нормальная серная кислота ,
немного ферроина
При 60 С изменение концентрации ионов церия приобретает характер релаксационных колебании - цвет раствора со временем периодически изменяется от красного (при избытке Се3+ ) до синего ( при избытке Се 4+) , рисунок 2.10а .
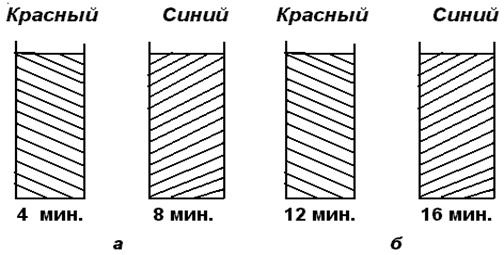
Рис. 2.10. Временные (а) и пространственные (б)
периодические структуры в реакции
Белоусова - Жаботинского.
...Такая система и эффект получили название химические часы . Если на реакцию Белоусова - Жаботинского накладывать возмущение - концентрационный или температурный импульс , то есть вводя несколько миллимолей бромата калия или прикасаясь к колбе в течении нескольких секунд , то после некоторого переходного режима будут снова совершаться колебания с такой же амплитудой и периодом , что и до возмущения . Диссипативная
Белоусова - Жаботинского , таким образом , является ассимптотически устойчивой . Рождение и существование незатухающих колебаний в такой системе свидетельствует о том , что отдельные части системы действуют согласованно с поддержанием определенных соотношений между фазами . При составе
сульфата церия - 4,0 ммоль/л,
бромида калия - 0,35 ммоль/л,
малоковой кислоты - 1,20 моль/л,
серной кислоты - 1,50 моль/л,
немного ферроина
при 20 С в системе происходят периодические изменения цвета с периодом около 4 минут . После нескольких таких колебаний спонтанно возникают неоднородности концентрации и образуются на некоторое время ( 30 минут ) , если не подводить новые вещества , устойчивые пространственные структуры , рисунок 2.10б . Если непрерывно подводить реагенты и отводить конечные продукты , то структура сохраняется неограниченно долго .
2.3.3. БИОЛОГИЧЕСКИЕ СИСТЕМЫ .
Животный мир демонстрирует множество высокоупорядоченных структур и великолепно функционирующих . Организм как целое непрерывно получает потоки энергии ( солнечная энергия , например , у растений ) и веществ ( питательных ) и выделяет в окружающую среду отходы жизнедеятельности . Живой организм - это система открытая . Живые системы при этом функционируют определенно в дали от равновесия . В биологических системах , процессы самоорганизации позволяют биологическим системам ²трансформировать² энергию с молекулярного уровня на макроскопический . Такие процессы , например , проявляются в мышечном сокращении , приводящим к всевозможным движениям , в образовании заряда у электрических рыб , в распознавании образов , речи и в других процессах в живых системах. Сложнейшие биологические системы являются одним из главных объектов исследования в синергетике . Возможность полного объяснения особенностей биологических систем , например , их эволюции с помощью понятий открытых термодинамических систем и синергетики в настоящее время окончательно неясна . Однако можно указать несколько примеров явной связи между понятийным и математическим аппаратом открытых систем и биологической упорядоченностью.
Более конкретно биологические системы мы рассмотрим в 3 главе , посмотрим динамику популяций одного вида и систему ²жертва - хищник² .
2.3.4. СОЦИАЛЬНЫЕ СИСТЕМЫ .
Социальная система представляет собой определенное целостное образование , где основными элементами являются люди , их нормы и связи . Как целое система образует новое качество , которое не сводится к сумме качеств ее элементов . В этом наблюдается некоторая аналогия с изменением свойств при переходе от малого к очень большому числу частиц в статической физике - переход от динамических к статическим закономерностям . При этом весьма очевидно , что всякие аналогии с физико - химическими и биологическими системами весьма условны , поэтому проводить аналогию между человеком и молекулой или даже нечто подобное было бы не допустимым заблуждением . Однако , понятийный и математический аппарат нелинейной неравновесной термодинамики и синергетики оказываются полезными в описании и анализе элементов самоорганизации в человеческом обществе.
Социальная самоорганизация - одно из проявлений спонтанных или вынужденных процессов в обществе , направленная на упорядочение жизни социальной системы , на большее саморегулирование. Социальная система является системой открытой способная , даже вынужденная обмениватся с внешним миром информацией , веществом , энергией. Социальная самоорганизация возникает как результат целеноправленных индивидуальных действий ее составляющих.
Рассмотрим самоорганизацию в социальной системы напримере урбанизации зоны . Проводя анализ урбанизации географических зон можно предположить , что рост локальной заселенности данной территории будет обусловлен наличием в этой зоне рабочих мест . Однако , здесь существует некоторая зависимость : состояние рынка , определяющего потребность в товарах и услугах и занятости . Отсюда возникает механизм нелинейной обратной связи в процессе роста плотности населения. Такая задача решается на основе логистического уравнения , где зона характеризуется ростом ее производительности N , новых экономических функций S - функция в локальной области i города. Логистическое уравнение описывает эволюцию численности населения и может быть тогда представлена в виде
dni
¾ = Кni(N + å Rk Sik - ni) - dni ( 2.13 )
dt k
где Rk вес данной к - ой функции , ее значимость . Экономическая функция изменяется с ростом численности : определяется спросом на к - й продукт в i - й области в зависимости от увеличения численности населения и конкуренции предприятий в других зонах города . Появление новой экономической функции играет роль социально экономической флуктуации и нарушает равномерное распределение плотности населения. Такие численные расчеты по логистическим уравнениям могут быть полезны прогнозировании многих проблем.
ПОСТАНОВКА ЗАДАЧИ.
В рассмотренных примерах в литературе имеются лишь общие выводы и заключения , не приведены конкретные аналитические расчеты или численные .
Целью настоящей дипломной работы является аналитические и численные исследования самоорганизации различных систем .
ГЛАВА 3
АНАЛИТИЧЕСКИЕ И ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ
САМООРГАНИЗАЦИИ РАЗЛИЧНЫХ СИСТЕМ.
Похожие работы
... и химическим процессам, происходящим в веществе, в различных системах. Важным достижением на пути этого процесса интеграции знаний было открытие фундаментального закона природы - закона сохранения и превращения энергии. Основатель термодинамики С. Карно в своем труде "Размышления о движущей силе огня и о машинах, способах развивать эту силу" пишет: "Тепло - это не что иное, как движущая сила, ...
... , или термодинамическое равновесие, при котором движение частиц хаотично. Максимальная энтропия означает полное термодинамическое равновесие, что эквивалентно хаосу. Часто второе начало термодинамики преподносится как объединенный принцип существования и возрастания энтропии. Принцип существования энтропии формулируется как математическое выражение энтропии термодинамических систем в условиях ...
... , не вызывая при этом никаких других изменений состояния системы. (Такую воображаемую машину принято называть вечным двигателем второго рода) 6. Обратимые и необратимые процессы По второму началу термодинамики в природе возможны процессы, при которых превращение теплоты в работу связано с компенсацией, и невозможны процессы, при которых такое превращение не сопровождается компенсацией. Это ...
... эффекта термодинамического процесса (2.5). Запишем: . (2.16) Выражение (2.16) и подобные ему, некоторые авторы называют обобщенной формулировкой I и II начала термодинамики. Преобразуем дифференциал , и подставим его в (2.5): . Из последнего равенства следует: , , . (2.17) Учитывая, что ...
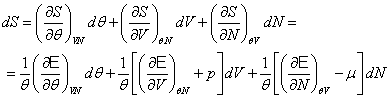
0 комментариев