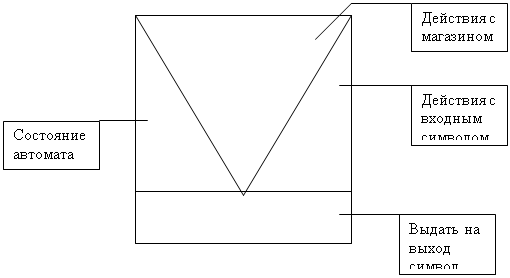
Навигация
В строке ...SiSj... символы Si и Sj входят в одну и ту
2. В строке ...SiSj... символы Si и Sj входят в одну и ту
└────┘
же свертываемую часть строки.Этот факт запишем в виде Si = Sj и
будем говорить, что Si и Sj входят в одно и то же свертывание.
3. В строке ...SiSj... свертываемая часть строки кончается
└──┘
символом Si, то есть Si - самый правый символ свертываемой части
строки. Это условие запишем в виде Si > Sj и будем говорить, что
Sj следует за Si.
Отношения <, =, > назовем отношениями предшествования. Отно-
шения предшествования обычно записываются в виде матрицы, стол-
бцы и строки которой соответствуют символам словаря V. На пересе-
чении i-ой строки и j-го столбца записывается отношение предшес-
твования между символами Si и Sj. Элементами матрицы являются
знаки <, =, > или пусто. Последний случай означает, что символы
Si и Sj ни в одной строке языка не могут стоять рядом.
В дальнейшем будет введено формальное определение отношений
предшествования и дан алгоритм их определения.
Сейчас же мы рассмотрим алгоритм анализа программы, разрабо-
танный Виртом и Вебером.
Достоинство этого алгоритма заключается в том, что он сни-
мает дополнительное ограничение на грамматику языка, и допускает,
чтобы в правилах грамматики два нетерминальных символа стояли ря-
дом. Но и в этом алгоритме требуется, чтобы между каждой парой
символов языка существовало не более одного отношения предшество-
вания и в множестве синтаксических правил не было двух одинако-
вых правых частей, т.е. правил, у которых правые части одинаковы,
а левые - разные.
Алгоритм основан на каноническом свертывании, т.е. на выде-
лении самой левой свертываемой части строки. Блок-схема алгорит-
ма показана на рис. 1 (@ - символ начального (конечного) ограни-
чителя входного анализируемого текста; не входит в алфавит языка).
┌────────────────────────────────┐
│ ^
┌─────┴───┬─┐ │
┌───────┬─┐ │ i:=i+1 │2│ │
│ i:=1 │1│ │ └─┤ │
│ └─┤ │ j:=i │ │
│ k:=2 │ │ │ │
│ │ │ R :=L │ │
│ R :=@ │ │ i k │ │
│ i │ │ │ │
└────┬────┘ │ k:=k+1 │ │
│ └────┬──────┘ │
│ │ │
│ ___│___ │
│ / │3\ ┌─────────┬──┐ │
│ / └──\ Да │ Конец │10│ │
│ / R равно @ \─────>┤ работы └──┤ │
│ \ i / │ алгорита │ │
│ \ / └────────────┘ │
│ \_______/ │
│ │ │
│ │ │
└───────────────────>─┤ │
┌───────────────────>─┤ Нет │
│ ___│____ │
│ / │4\ │
│ / └──\ Нет │
│ / R > L \__________________________│
│ \ i k /
│ \ ? /
│ \________/
│ Да│
│ ├<────────────────────┐
│ ____│______ │
│ / │5\ │
│ / └──\ ┌─────┴───┬─┐
│ / R = R \______│ │6│
│ \ j-1 j / Да │ j:=j-1 └─┤
│ \ / │ │
│ \___________/ └───────────┘
│ │Нет
│ ┌────────┴─────┬─┐
│ │ │7│
│ │ U < R ... R└─┤
│ │ j i │
│ └────────┬───────┘
│ │
│ │
│ ┌───────┴─────┬─┐
│ │ │8│
│ │ Переход на └─┤
│ │ семантические │
│ │ подпрограммы │
│ │ │
│ └───────┬───────┘
│ │
│ ┌───────┴────┬─┐
│ │ i:=j │9│
└───────────────┤ R :=u └─┤
│ i │
└──────────────┘
Рис. 1. Блок-схема алгоритма свертывания
В начале анализа строки в верхнюю ячейку магазина записы-
вается первый символ программы, т.е. символ "@" (блок 1).
Затем находится самый правый символ самой левой свертывае-
мой части строки (блок 4). Для этого по матрице предшествования,
которая составляется заранее, проверяют отношения предшествова-
ния между символом, находящимся в верхней ячейке магазина Ri, и
очередным входным символом строки Lk. Если условие Ri > Lk не вы-
полняется, то очередной входной символ записывается в верхушку
магазина (блок 2) и процесс продолжается до тех пор, пока не бу-
дет выполнено условие Ri > Lk, т. е. не будет найден самый пра-
вый символ самой левой свертываемой части строки.
Затем находится самый левый символ этой свертываемой части
строки. Для этого проверяется отношение предшествования между
каждой парой символов Rj-1 = Rj, записанных в магазине (блоки 5 и
6). Нарушение условия Ri = Rj означает, что свертываемая часть
строки кончилась и последовательность символов Rj...Ri есть са-
мая левая свертываемая часть строки.
У каждого нетерминального символа может быть несколько са-
мых левых и самых правых символов.
По таблице, имеющейся в трансляторе, в которой записаны
правила свертывания, производится свертывание (блок 7) и управ-
ление передается на соответствующую семантическую подпрограмму.
Семантическая подпрограмма генерирует программу на выходном язы-
ке, соответствующую данному синтаксическому правилу (блок 8).
После того, как генерирование соответствующего куска выход-
ной программы закончено, символы Rj...Ri "выталкиваются" из мага-
зина и в его верхнюю ячейку записывается символ u (блок 9).
Процесс продолжается до тех пор, пока в верхней ячейке мага-
зина не будет обнаружен символ "@" (блок 3), определяющий конец
программы.
Для анализа ошибок в алгоритм включены следующие блоки:
Блок 11 проверяет, могут ли символы Rj и Lk стоять в строке
рядом. Если в матрице предшествования (i,j)-ый элемент пуст (знак
_), то символы Si и Sj стоять рядом не могут и осуществляется пе-
реход к блоку 15. Иначе управление передается в блок 4.
Блок 12 проверяет значение величины j: если j=1, то должно
производиться сравнение с символом "@", что по алгоритму анализа
вообще быть не может. В этом случае переход к блоку 15. Если j не
равно 1, то переход к блоку 5.
Блок 13 проверяет, есть ли правило с правой частью Rj...Ri в
грамматике языка. Если да,переход к блоку 7, иначе - к блоку 15.
Блок 14 проверяет, есть ли правило Rj...Ri. Если да, то ал-
горитм анализа и свертывания входного текста закончен (переход к
блоку 10); иначе в тексте есть ошибка, из-за которой он не может
быть свернут (переход к блоку 15).
Блок 15 выводит сообщение об ошибке и переходит к анализу
следующего оператора.
Таким образом, сложный анализ входного текста, написанного
на входном языке, реализуется простым алгоритмом.
Требование единственности отношений предшествования вызы-
вает необходимость перестройки грамматики языка. Устранение этой
неоднозначности иногда становится достаточно трудоемкой задачей.
Мак-Киман разработал алгоритм анализа входного текста, который не
предъявляет к грамматике языка требования однозначности отноше-
ний предшествования.
Для определения границ сворачиваемой строки он использует не
одну, а две матрицы: первую - для нахождения самого правого сим-
вола строки - назовем М1, и вторую - для нахождения самого лево-
го символа строки - М2. В М1 заносятся следующие отношения пред-
шествования: <= (< или =), > и >=< (последнее означает > и либо
=, либо <). B M2 заносятся отношения предшествования => (> или =),
< и <=> (последнее означает < и либо =, либо >).
При поиске самого правого символа безразлино, какое от ноше-
ние предшествование <, = или <= находиться между двумя анализи-
руемыми символами. Аналогично при поиске самого левого символа
безразлично, какое отношение предшествование >, = или => находит-
ся между двумя анализируемыми символами. Поэтому эти отношения в
соответствующих матрицах не различаются. В тех случаях, когда
между парой символов существуеют отношения >=<, при поиске гра-
ниц сворачиваемой строки необходима дополнительная информация.
Эта информация задается в виде логических функций трех аргументов.
При поиске самого правого символа сворачиваемой строки с
помощью матрицы М1 используется функция
| истина, если Si > Lk;
Р1(Si-1, Si, Lk) = <
| ложь в противном случае.
Функция Р1 истинна, если в контексте Si-1SiLk символ Si яв-
ляется самым правым символом сворачиваемой строки ...Si-1Si.
Здесь Si - символ, хранящийся в верхней ячейке стека, Si-1 -сим-
вол, хранящийся в следующейся ячейке стека и Lk - очередной сим-
вол анализируемого текста.
Таким образом, каждой паре символов, у которых в М1 записа-
но отношение >=<, ставится в соответствие несколько функций Р1,
позволяющих анализировать уже не пару, а тройку символов для оп-
ределение правил границы сворачиваемой строки. Но эта тройка уже
должна быть определена так, чтобы ответ был однозначный.
Аналогично при поиске самого левого символа сворачиваемой
строки с помощью матрицы М2 используется функция
| истина, если Sj-1 < Sj;
Р2(Sj-1, Sj, Sj+1) = <
| ложь в противном случае.
B контексте Sj-1SiSj+1 символ Sj является самым левым симво-
лом сворачиваемой строки SjSj+1... . Здесь Sj-1, Sj, Sj+1 - сим-
волы, хранящийся в j-1, j и j+1 ячейках стека.
Каждой паре символов, у которых в М2 записано отношение <=>,
ставится в соответствие несколько функций Р2, позволяющих, как и
функции Р1, анализировать не пару, а тройку символов. Но эта
тройка уже должна быть определена так, чтобы ответ был однознач-
ный.
Блок-схема алгоритма анализа входного текста с помощью мат-
риц предшествования и функций Р1 и Р2 приведена на рис. 2. Буквы
i и j обозначают номера ячеек магазина, k - номер очередного сим-
вола входного текта, Ri и Rj- символы, находящиеся в i-х и j-х
ячейках магазина, Lk - k-й символ входного текста. В начале ана-
лиза строки в верхнюю ячейку магазина записывается первый символ
программы, т.е. символ "@" (блок 1). Затем производится проверка
на конец программы (блок 3). Если Lk = @, то выполнение програм-
мы окончено и осуществляется переход к блоку 14. Если Lk не сов-
падает @, осуществляется переход к блоку 4.
Производится поиск самого правого символа самой левой свер-
тываемой строки. Для этого по М1 проверяется отношение предшес-
твования между символами Lk и Ri (блок 4). Если это отношение
равно <=, т.е. Ri не является самым правым символом сворачивае-
мой строки, то производится запись очередного символа в магазин
(блок 2).
Если между символами Ri и Lk существует отношение <=>, то
блоком 5 проверяется функция Р1 для двух верхних символов магази-
на и очередного символа входного текста. При значении функции Р1
- ложь (на рис. 2), это значение обозначено Л, т.е. если Ri не
является самым правым символом, осуществляется переход к блоку 2.
Если значение Р1 - истина (И), т.е. Ri - самый правый символ
строки, то осуществляется переход к блоку 6.
Блоком 6 начинается поиск самого левого символа свертывае-
мой строки; j присваивается значение i. По М2 определяется отно-
шение между символами Rj-1 и Rj (блок 7). Если отношение есть =>,
т.е. Rj не является самым левым символом свертываемой строки, то
j := j-1 (блок 8) и определяется отношение между следующей парой
символов. Если отношение есть <, т.е. Rj-1 является самым левым
символом, осуществляется переход к блоку 10. Блок 10 введен для
того, чтобы в блоке 11 свертывание всегда происходило от j-го до
i-го элемента.
Если между символами Rj-1 и Rj отношение >=<, то проверяет-
ся функция Р2 для трех символов, находящихся в j-1, j и j+1-й
ячейках магазина. Если значение Р2 - Л (Rj не является самым ле-
вым символом), осуществляется переход к блоку 8; если значение Р2
- И (Rj является самым левым символом), то осуществляется пере-
ход к блоку 11.
Блоки 11,12 и 13 производят свертывание, переход на генери-
рующую подпрограмму и запись вновь полученного нетерминального
символа U в верхнюю ячейку магазина. Они в точности соответ-
ствуют блокам 7, 8, 9 на рис. 1. На рис. 1. не показаны блоки
анализа синтаксических ошибок. Они аналогичны соответствующим
блокам на рис. 2.
Метод Мак-Кимана освобождает от ограничения однозначности
отношений предшествования, накладываемого методом Вирта, но он
требует, естественно, больших объeмов памяти для записи матриц и
функции. В трансляторе с одной из версий языка PL/1 для машин се-
рии IBM-360 М1 составила 90x45 элементов, М2-90x90. Каждый эле-
мент занимает 2 бита. Число функций Р1 и Р2 приближалось к 450.
ЛЕКЦИЯ 4
ПОСТРОЕНИЕ МАТРИЦ ПРЕДШЕСТВОВАНИЯ
И ПРЕОБРАЗОВАНИЕ ГРАММАТИК
Рассмотрим алгоритм составления матрицы предшествования. Для
этого дадим формальные определения отношений предшествования и
множество самых левых и самых правых символов.
1. Для любой упорядоченной пары символов (Si, Sj) Si = Sj
тогда и только тогда, когда существует синтаксическое правило ти-
па U::=xSiSjy для некоторого символа U и некоторых строк x и y.
2. Для любой упорядоченной пары символов (Si,Sj) Si < Sj
тогда и только тогда, когда существует синтаксическое правило ти-
па U::= xSiUly для некоторых U, Ul, x, y и порождение Ul -> Sjz
для некоторой строки z.
3. Для любой упорядоченной пары символов (Si, Sj) Si > Sj
тогда и только тогда, когда:
a) существует синтаксическое правило типа U ::= xUkSjy для
некоторых U, Uk, x, y и порождение Uk -> zSi для некоторой стро-
ки z или
б) существует синтаксическое правило типа U ::= xUkUly для
некоторых U, Uk, Ul, x, y и порождения Uk -> zSi, Ul -> Sjw для
некоторых строк z и w.
Строки x,y,z,w могут быть пустыми.
Похожие работы
... работы. В ходе работы над дипломным проектом разработан транслятор. Проблема создания такого транслятора является очень актуальной, т.к. многим пользователям САПР необходимо доступ к технической документацию, которую удобнее хранить на удаленных серверах в формате HTML. Поэтому степень положительного эффекта от выполнения дипломного проекта научно-исследовательского характера 1=6.5. В ...
... направления, активно развиваемого сейчас в разных коллективах и странах. Отталкиваясь от трансформационной модели смешанных вычислений и от своих работ в области трансляции и оптимизации программ, Ершов определяет концепцию трансформационной машины. Трансформационная машина есть абстрактное вычислительное устройство, выполняющее программы в некотором "сверхязыке", действиями которого являются ...
... 166, 16 Mb RAM, Windows 95 Вывод В ходе разработки курсового проекта я ближе ознакомился с теорией МП- трансляторов, научился писать программы - конструкторы для построения МП – транслятора по его параметрам с последующей проверкой задаваемых цепочек, закрепил знания по системному программированию. Разрабатывая программу, я научился применять знания дискретной математике, что облегчает ...
... позволяет связывать твёрдотельные модели, сборки или чертежи, созданные с помощью SolidWorks 97, с файлами других приложений, что значительно расширяет возможности автоматизации процесса проектирования. С помощью технологии OLE можно использовать информацию, полученную в других приложениях Windows, для управления моделями и чертежами SolidWorks. Например, размеры модели могут быть рассчитаны в ...


0 комментариев