Навигация
Оператор сдвига. Спектр оператора сдвига
6. Оператор сдвига. Спектр оператора сдвига
Определение 7. Ограниченный линейный оператор U в пространстве Н называется изометрическим, если он не изменяет величины скалярного произведения: ![]() для любых
для любых ![]() .
.
В этом случае, если х=у, то ![]() , или
, или ![]() . Значит, изометрический оператор сохраняет норму элемента, а норма самого такого оператора, как следует из определения нормы, равна 1 (
. Значит, изометрический оператор сохраняет норму элемента, а норма самого такого оператора, как следует из определения нормы, равна 1 (![]() ).
).
Понятие изометрического оператора можно ввести также для операторов, действующих в нормированном пространстве.
Определение 8. Ограниченный линейный оператор U в нормированном пространстве Е называется изометрическим, если он не изменяет величины нормы: ![]() для любых
для любых ![]() .
.
Лемма 1. Для того, чтобы линейный оператор U в пространстве Н был изометрическим, необходимо и достаточно, чтобы выполнялось условие: ![]() для любых
для любых ![]() .
.
Доказательство. Нужно доказать только достаточность. Для этого используем тождество ![]()
![]()
![]()
![]()
![]() . Его легко проверить, если представить левую часть в виде скалярных произведений:
. Его легко проверить, если представить левую часть в виде скалярных произведений: ![]()
![]()
![]()
![]()
![]() . Так как левая часть не изменится при замене векторов
. Так как левая часть не изменится при замене векторов ![]() на векторы
на векторы ![]() , то правая тоже не изменится, т. е.
, то правая тоже не изменится, т. е. ![]() .
.
Определение 9. Оператор U называется унитарным, если он изометрический и имеет обратный оператор, определенный на всем пространстве Н.
Теорема 7. Спектр унитарного оператора – это множество, лежащее на единичной окружности.
Доказательство. Доказательство проведем в два этапа:
Докажем, что спектр унитарного оператора U содержится в единичном круге.
Рассмотрим обратный оператор и покажем, что он тоже унитарный. Докажем, что, если ![]() принадлежит спектру оператора U, то
принадлежит спектру оператора U, то ![]() принадлежит спектру обратного оператора и наоборот.
принадлежит спектру обратного оператора и наоборот.
Для доказательства I этапа применим теорему 4: если А – ограниченный линейный оператор в нормированном пространстве и ![]() , то
, то ![]() – регулярная точка. Иначе говоря, спектр оператора А содержится в круге радиуса
– регулярная точка. Иначе говоря, спектр оператора А содержится в круге радиуса ![]() с центром в нуле. А норма унитарного оператора U, как было показано, равна 1 (
с центром в нуле. А норма унитарного оператора U, как было показано, равна 1 (![]() ). Следовательно, спектр унитарного оператора содержится в единичном круге.
). Следовательно, спектр унитарного оператора содержится в единичном круге.
Перейдем ко II этапу. Докажем, что оператор, обратный к унитарному оператору, также унитарный оператор. Покажем, что он удовлетворяет условию изометрии: ![]() для всех
для всех ![]() . Положим Ux=y, тогда
. Положим Ux=y, тогда ![]() , и
, и ![]() , т. е.
, т. е. ![]() для всех
для всех ![]() .
.
Докажем, что, если точка ![]() является регулярной для оператора U, то точка
является регулярной для оператора U, то точка ![]() является регулярной для обратного оператора U-1. Точка
является регулярной для обратного оператора U-1. Точка ![]() , является регулярной для оператора U, если выполняется условие:
, является регулярной для оператора U, если выполняется условие:
![]() (*).
(*).
Оператор U-1 является обратным для оператора U, значит, для них верно U-1U=I=UU-1 . Используя это, равенство (*) можно переписать:
![]() , или
, или
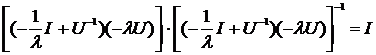 .
.
Используем свойство обратных операторов: оператор, обратный произведению операторов, равен произведению обратных операторов к данным, взятых в противоположном порядке, т.е. для двух операторов А и В имеем ![]() . Тогда равенство можно переписать в виде:
. Тогда равенство можно переписать в виде:
![]() .
.
Вычислим отдельно произведение:
![]() .
.
В итоге ![]() , т.е.
, т.е. ![]() является регулярной для обратного оператора U-1.
является регулярной для обратного оператора U-1.
Возьмем множество точек ![]() . Тогда точки вида
. Тогда точки вида ![]() лежат вне единичного круга и все являются для оператора
лежат вне единичного круга и все являются для оператора ![]() регулярными, так как он унитарный и его норма равна 1. Но поскольку оператор
регулярными, так как он унитарный и его норма равна 1. Но поскольку оператор ![]() - обратный к оператору
- обратный к оператору ![]() , то точки, входящие в
, то точки, входящие в ![]() , по предыдущему рассуждению являются для него регулярными. Следовательно, спектр оператора U – это множество, лежащее на единичной окружности.
, по предыдущему рассуждению являются для него регулярными. Следовательно, спектр оператора U – это множество, лежащее на единичной окружности.
Важным примером изометрического оператора является оператор сдвига.
Определение 10. Оператор ![]() , заданный в пространстве последовательностей, называется оператором сдвига, если он каждую последовательность вида (х1,х2,…, хn…) переводит в последовательность вида (0, х1, х2, …, хn…), т.е. выполняется равенство:
, заданный в пространстве последовательностей, называется оператором сдвига, если он каждую последовательность вида (х1,х2,…, хn…) переводит в последовательность вида (0, х1, х2, …, хn…), т.е. выполняется равенство: ![]() (х1,х2,…, хn…)=(0, х1, х2, …, хn…).
(х1,х2,…, хn…)=(0, х1, х2, …, хn…).
Можно также рассматривать оператор сдвига, который действует в пространстве последовательностей, бесконечных в обе стороны. Элемент этого пространства можно представить в таком виде: (…х-2, х-1, х0, х1, х2, …).
Определение 11. Оператор ![]() называется оператором двухстороннего сдвига, если он каждую последовательность, бесконечную в обе стороны, сдвигает вправо, т.е. выполняется равенство:
называется оператором двухстороннего сдвига, если он каждую последовательность, бесконечную в обе стороны, сдвигает вправо, т.е. выполняется равенство: ![]() .
.
Уточним, о каких пространствах последовательностей будет идти речь:
1) l2 – пространство односторонних последовательностей комплексных чисел с натуральной нумерацией, для которых ряд ![]() - сходящийся. Скалярное произведение в этом пространстве определяется формулой
- сходящийся. Скалярное произведение в этом пространстве определяется формулой ![]() .
.
2) l2(-∞;∞) – пространство двусторонних последовательностей комплексных чисел с нумерацией целыми числами, для которых соответственно ряд ![]() – сходящийся. Скалярное произведение в этом пространстве определяется формулой
– сходящийся. Скалярное произведение в этом пространстве определяется формулой ![]() .
.
Рассмотрим оператор одностороннего сдвига U(x1, x2, …, xn, …)=(0, x1, x2, …). Покажем, что этот оператор является изометрическим. Действительно, для любых ![]()
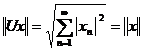 . А, значит, этот оператор по лемме 1 является изометрическим. Указанный оператор U не является унитарным, так как его образ – это не все пространство l2; векторы, имеющие ненулевую первую координату (например векторы вида (1, х1, х2, …)) не имеют прообраза. Значит, обратного оператора он не имеет.
. А, значит, этот оператор по лемме 1 является изометрическим. Указанный оператор U не является унитарным, так как его образ – это не все пространство l2; векторы, имеющие ненулевую первую координату (например векторы вида (1, х1, х2, …)) не имеют прообраза. Значит, обратного оператора он не имеет.
Теорема 8. Оператор двухстороннего сдвига является унитарным оператором
Доказательство. Рассмотрим оператор двустороннего сдвига
U(…, x-1, x00, x1, …)=(…, x-2, x-10, x0, x1, …).
Очевидно, что этот оператор сохраняет норму, т.е. является изометрическим: ![]() . Покажем, что он имеет обратный оператор – это оператор, который любую последовательность сдвигает влево.
. Покажем, что он имеет обратный оператор – это оператор, который любую последовательность сдвигает влево.
В пространстве последовательностей, как и в любом метрическом пространстве, любой вектор представляется как линейная комбинация элементов базиса. В этом пространстве имеется канонический базис – это последовательности вида
………………………
l-1=(.., 0, 1-1, 0, …)
l0=(…, 0, 10, 0, …)
l1=(…, 0, 11, 0, …)
………………………
Подействуем оператором U на произвольный элемент базиса:
Ulk=U(…, 0, 1k, 0,…)=(…, 0, 1k+1, 0)=lk+1.
Т.е. каждый элемент базиса оператор U переводит в последующий элемент. Чтобы осуществлялось обратное действие, мы должны каждый элемент базиса перевести в предыдущий элемент, т.е. U-1lk=lk-1.
Каждый вектор пространства l2 х=(…, х-1, х0, х1, …) может быть представлен в виде: ![]() . А так как оператор U-1 элементы базиса переводит в предыдущие, то, действуя на последовательность
. А так как оператор U-1 элементы базиса переводит в предыдущие, то, действуя на последовательность ![]() , сдвинет ее влево.
, сдвинет ее влево.
Итак, мы получили, что оператор двухстороннего сдвига U имеет обратный оператор и является изометрическим, следовательно, он является унитарным. Спектр этого оператора лежит на единичной окружности.
7.Взвешенные сдвиги
Определение 12. Оператором взвешенного сдвига называется произведение оператора сдвига (одностороннего или двустороннего) на диагональный (в этом же базисе) оператор.
Более подробно: пусть ![]() – ортонормированный базис (n = 0, 1, 2, … или n = 0,
– ортонормированный базис (n = 0, 1, 2, … или n = 0, ![]() 1,
1, ![]() 2, …) и пусть
2, …) и пусть ![]() – ограниченная последовательность комплексных чисел (n пробегает те же значения, что и выше). Оператором взвешенного сдвига называется оператор вида SP, где S– оператор сдвига (Sln= ln+1) ,а Р – диагональный оператор с диагональю
– ограниченная последовательность комплексных чисел (n пробегает те же значения, что и выше). Оператором взвешенного сдвига называется оператор вида SP, где S– оператор сдвига (Sln= ln+1) ,а Р – диагональный оператор с диагональю ![]() (Pln =
(Pln = ![]() ln ).
ln ).
Найдем выражение для нормы и спектрального радиуса оператора взвешенного сдвига через его веса.
Вспомним, что сдвиг S1 – изометрический оператор, значит, не изменяет нормы элемента: ![]() для любого
для любого ![]() .Поэтому норма оператора А равна норме соответствующего диагонального оператора: для любого
.Поэтому норма оператора А равна норме соответствующего диагонального оператора: для любого ![]()
![]() и
и ![]() . Найдем норму диагонального оператора Pln =
. Найдем норму диагонального оператора Pln = ![]()
![]() , где
, где ![]() – некоторая ограниченная последовательность комплексных чисел. Рассмотрим произвольную последовательность
– некоторая ограниченная последовательность комплексных чисел. Рассмотрим произвольную последовательность ![]() с единичной нормой:
с единичной нормой: 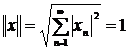 . При этом в базисе
. При этом в базисе ![]() элемент
элемент ![]() имеет разложение
имеет разложение 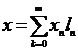 . Подействуем на элемент х оператором Р:
. Подействуем на элемент х оператором Р: 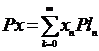
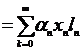 . При этом
. При этом 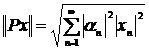
![]()
![]()
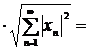
![]() . Отсюда следует, что
. Отсюда следует, что ![]()
![]() . Покажем, что выполняется также и обратное неравенство. Если для последовательности
. Покажем, что выполняется также и обратное неравенство. Если для последовательности ![]()
![]() достигается, т.е.
достигается, т.е. ![]() при некотором
при некотором ![]() , то возьмем элемент
, то возьмем элемент ![]() :
: ![]()
![]() ,
, ![]()
![]() . Если же
. Если же ![]() не достигается, то можно взять подпоследовательность
не достигается, то можно взять подпоследовательность ![]()
![]() , тогда
, тогда ![]()
![]() . Это говорит о том, что не может быть
. Это говорит о том, что не может быть ![]()
![]() . Итак,
. Итак, ![]()
![]() и
и ![]()
![]() . Мы получили, что норма оператора взвешенного сдвига равна точной верхней грани модулей его весов.
. Мы получили, что норма оператора взвешенного сдвига равна точной верхней грани модулей его весов.
Чтобы найти спектральный радиус оператора взвешенного сдвига, найдем нормы его степеней. Вычислим степени оператора А: Aln = ![]() , A2ln =
, A2ln = ![]() ,A3ln =
,A3ln = ![]() , и так далее. Следовательно, Ак можно представить в виде произведения изометрии (к-й степени оператора сдвига) и диагонального оператора, у которого n-й диагональный член равен произведению к последовательных чисел
, и так далее. Следовательно, Ак можно представить в виде произведения изометрии (к-й степени оператора сдвига) и диагонального оператора, у которого n-й диагональный член равен произведению к последовательных чисел ![]() , начиная с
, начиная с ![]() . Значит,
. Значит, 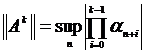 , отсюда,
, отсюда, 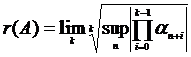 .
.
Похожие работы
... непрерывных и ограниченных функций – C[], заданный следующим образом: Af(x) = f(x+a). Функции f(x), f(x+a) C[], a R, f(x+a) – непрерывная и ограниченная функция. Покажем линейность оператора А, по определению 1 должны выполняться следующие аксиомы : 1) Аксиома аддитивности: А(f+g) = А(f) + А(g). А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g). По определению суммы функции, аксиома ...
... В этих формулах привлекательно то, что результат произведения двух операторов сдвигов выражается через операторы с действительными собственными значениями, как это следует из сопоставления правых частей уравнений (4.92) – (4.94), с одной стороны, и уравнений (4.90) и (4.91) – с другой. 4.3.5.13. Все коммутационные соотношения операторов момента импульса и его проекций, найденные в этом разделе,
... проектора Q пространства L на H, что tQ = Qt для любого вещественного s. (4). Найдем вид проектора. Положим e(x)=e . Тогда te=ee, а так как оператор Q линеен, то Qte = eQe. (5). Из (4) и (5) следует, что (Qe)(x-s) = e (Qe)(x). (6). Пусть С = (Qe)(0). При Q = 0 соотношение (6) имеет вид Qe = Ce. ...
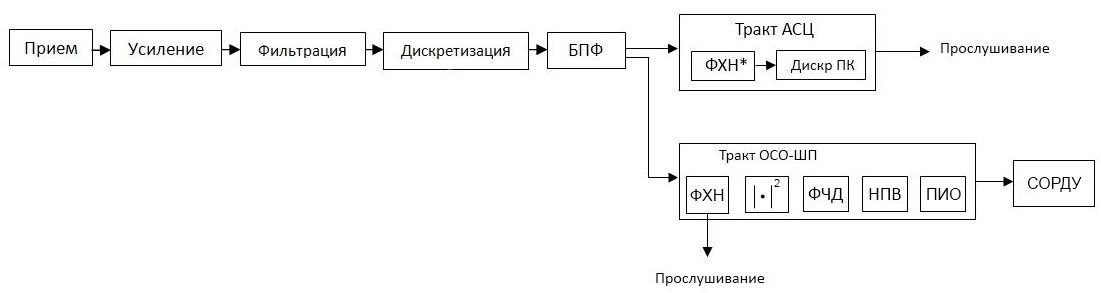
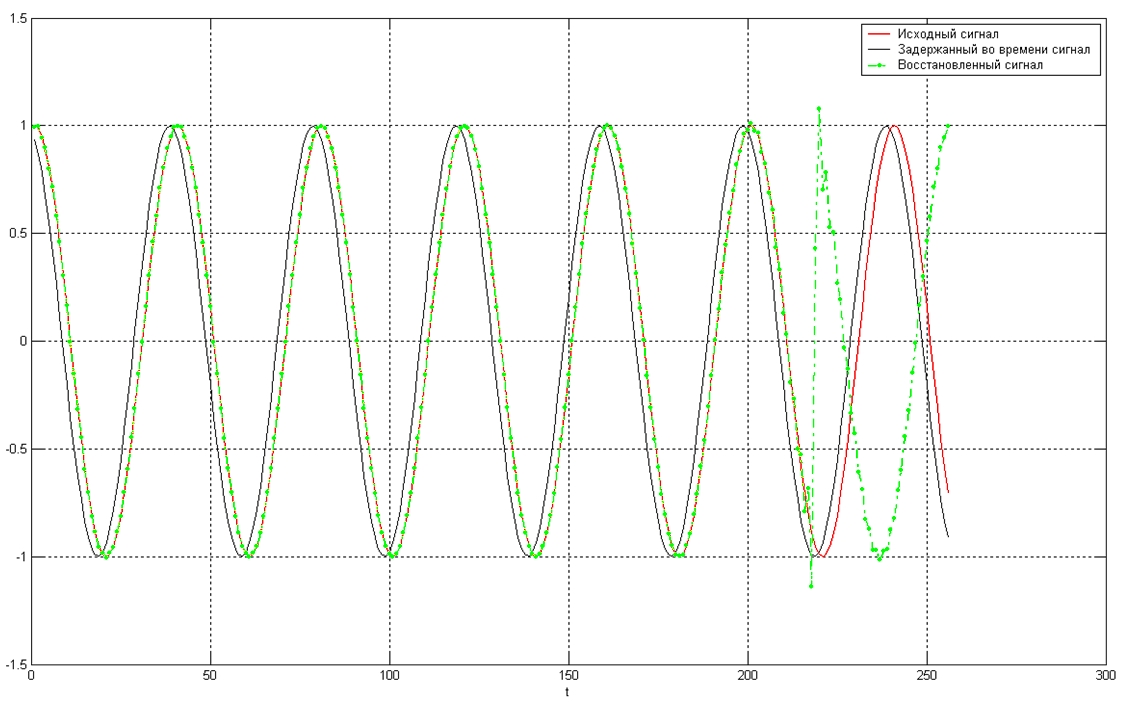
... частотного диапазона и внешний вид фильтра. То же самое мы видим и для других Частотных диапазонов на плакатах 2 и 3 . Доклад окончен Тема: Модель тракта прослушивания гидроакустических сигналов ОглавлениеВведение Место тракта прослушивания в структуре режима ШП типовой ГАС Формирование канала наблюдения в частотной области 3 Факторы, влияющие на восстановление сигнала 3.1 Перекрытие входных ...
0 комментариев