Навигация
4. Обратный оператор
Пусть А – линейный оператор, действующий из Е в Е1 , и DA область определения, а RA – область значений этого оператора.
Определение 6. Оператор А называется обратимым, если для любого у![]() RA уравнение Ах=у имеет единственное решение.
RA уравнение Ах=у имеет единственное решение.
Если А обратим, то любому элементу у![]() RA можно поставить в соответствие единственный элемент х
RA можно поставить в соответствие единственный элемент х![]() DA , являющийся решением уравнения Ах=у. Оператор, осуществляющий это соответствие, называется обратным к А и обозначается А-1.
DA , являющийся решением уравнения Ах=у. Оператор, осуществляющий это соответствие, называется обратным к А и обозначается А-1.
Теорема 3 [1]. Оператор А-1, обратный линейному оператору А, также линеен.
Доказательство.
Достаточно проверить выполнение равенства
![]() .
.
Положим Ах1=у1 и Ах2=у2, в силу линейности А имеем
![]() (*)
(*)
По определению обратного оператора А-1у1=х1 и А-1у2=х2, умножим оба равенства соответственно на ![]() и
и ![]() :
:
![]() .
.
С другой стороны из равенства (*) следует ![]() , следовательно,
, следовательно, ![]() .
.
Теорема доказана.
Теорема 4 [3]. (Теорема Банаха об обратном операторе)
Пусть А – линейный ограниченный оператор, взаимно однозначно отображающий банахово пространство Е на банахово пространство Е1. Тогда обратный оператор А-1 ограничен.
Теорема 5 [3]. Пусть Е – банахово пространство, I – тождественный оператор в Е, а А – такой ограниченный линейный оператор, отображающий Е в себя, что ![]() . Тогда оператор (I-A)-1 существует, ограничен и представляется в виде
. Тогда оператор (I-A)-1 существует, ограничен и представляется в виде 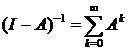 .
.
Доказательство.
Так как ![]() , то ряд
, то ряд 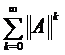 сходится. А так как
сходится. А так как ![]() для всех
для всех ![]() , то ряд
, то ряд 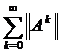 также сходится. Пространство Е полно, значит, из сходимости ряда
также сходится. Пространство Е полно, значит, из сходимости ряда 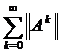 вытекает, что сумма ряда
вытекает, что сумма ряда 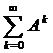 представляет собой ограниченный линейный оператор. Для любого n имеем:
представляет собой ограниченный линейный оператор. Для любого n имеем: 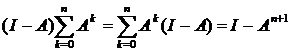 , переходя к пределу и учитывая, что
, переходя к пределу и учитывая, что ![]() , получаем
, получаем 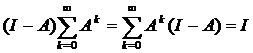 , следовательно
, следовательно 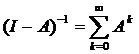 .
.
Теорема доказана.
5. Спектр оператора. Резольвента.
Всюду, где речь идет о спектре оператора, считаем, что оператор действует в комплексном пространстве.
В теории операторов и ее применениях первостепенную роль играет понятие спектра оператора. Рассмотрим это понятие сначала применительно к операторам в конечномерном пространстве.
Пусть А – линейный оператор в n-мерном пространстве Еn . Число ![]() называется собственным значением оператора А , если уравнение
называется собственным значением оператора А , если уравнение![]() имеет ненулевые решения. Совокупность всех собственных значений называется спектром оператора А, а все остальные значения
имеет ненулевые решения. Совокупность всех собственных значений называется спектром оператора А, а все остальные значения ![]() – регулярными.
– регулярными.
Иначе говоря, ![]() есть регулярная точка, если оператор
есть регулярная точка, если оператор ![]() обратим. При этом оператор
обратим. При этом оператор ![]() -1 , как и любой оператор в конечномерном пространстве, ограничен, поэтому в конечномерном пространстве существует две возможности:
-1 , как и любой оператор в конечномерном пространстве, ограничен, поэтому в конечномерном пространстве существует две возможности:
уравнение ![]() имеет ненулевое решение, т. е.
имеет ненулевое решение, т. е. ![]() есть собственное значение для А , оператор
есть собственное значение для А , оператор ![]() -1 при этом не существует;
-1 при этом не существует;
существует ограниченный оператор ![]() -1, т.е.
-1, т.е. ![]() есть регулярная точка.
есть регулярная точка.
В бесконечномерном пространстве существует третья возможность:
оператор ![]() -1 существует, т.е. уравнение
-1 существует, т.е. уравнение ![]() имеет лишь нулевое решение, но этот оператор не ограничен.
имеет лишь нулевое решение, но этот оператор не ограничен.
Введем следующую терминологию. Число ![]() мы назовем регулярным для оператора А, действующего в (комплексном) линейном нормированном пространстве Е, если оператор
мы назовем регулярным для оператора А, действующего в (комплексном) линейном нормированном пространстве Е, если оператор ![]() -1 , называемый резольвентой оператора А , определен на всем Е и непрерывен. Совокупность всех остальных значений
-1 , называемый резольвентой оператора А , определен на всем Е и непрерывен. Совокупность всех остальных значений ![]() называется спектром оператора А . Спектру принадлежат все собственные значения оператора А, так как если
называется спектром оператора А . Спектру принадлежат все собственные значения оператора А, так как если ![]() х=0 при некотором
х=0 при некотором ![]() , то
, то ![]() -1 не существует. Их совокупность называется точечным спектром. Остальная часть спектра, т.е. совокупность тех
-1 не существует. Их совокупность называется точечным спектром. Остальная часть спектра, т.е. совокупность тех ![]() , для которых
, для которых ![]() -1 существует, но не непрерывен, называется непрерывным спектром. Итак, любое значение
-1 существует, но не непрерывен, называется непрерывным спектром. Итак, любое значение ![]() является для оператора А или регулярным, или собственным значением, или точкой непрерывного спектра. Возможность наличия у оператора непрерывного спектра – существенное отличие теории операторов в бесконечномерном пространстве от конечномерного случая.
является для оператора А или регулярным, или собственным значением, или точкой непрерывного спектра. Возможность наличия у оператора непрерывного спектра – существенное отличие теории операторов в бесконечномерном пространстве от конечномерного случая.
Теорема 6 [3]. Если А –ограниченный линейный оператор в банаховом пространстве и ![]() , то
, то ![]() – регулярная точка.
– регулярная точка.
Доказательство.
Так как, очевидно ![]() , то
, то 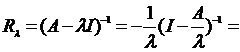
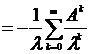 . При
. При ![]() этот ряд сходится (теорема 4), т.е. оператор
этот ряд сходится (теорема 4), т.е. оператор ![]() имеет ограниченный обратный. Иначе говоря, спектр оператора А содержится в круге радиуса
имеет ограниченный обратный. Иначе говоря, спектр оператора А содержится в круге радиуса ![]() с центром в нуле.
с центром в нуле.
Теорема доказана.
Пример. В пространстве ![]() функций, непрерывных на отрезке
функций, непрерывных на отрезке ![]() , рассмотрим оператор А, определяемый формулой Аx(t)=M(t)x(t) , где M(t)– фиксированная непрерывная функция. Возьмем произвольное число
, рассмотрим оператор А, определяемый формулой Аx(t)=M(t)x(t) , где M(t)– фиксированная непрерывная функция. Возьмем произвольное число ![]() , тогда
, тогда ![]() , а
, а ![]() .
.
Спектр рассматриваемого оператора состоит из всех ![]() , для которых Если функция M(t)-
, для которых Если функция M(t)- ![]() обращается в нуль при некотором t, заключенном между 0 и 1, то оператор
обращается в нуль при некотором t, заключенном между 0 и 1, то оператор ![]() не определен на всем пространстве
не определен на всем пространстве ![]() , так как функция
, так как функция 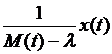 уже не обязана быть непрерывной. Если же функция M(t)-
уже не обязана быть непрерывной. Если же функция M(t)- ![]() не обращается в нуль на отрезке
не обращается в нуль на отрезке ![]() , то функция
, то функция 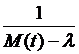 непрерывна на этом отрезке, а, следовательно, ограничена: для некоторого
непрерывна на этом отрезке, а, следовательно, ограничена: для некоторого ![]()
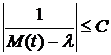 при всех
при всех ![]() . Следовательно, оператор
. Следовательно, оператор ![]() ограничен, а число
ограничен, а число ![]() – регулярное для оператора А. Таким образом, спектр оператора А есть совокупность всех значений функции M(t) на отрезке [0;1], причем собственные значения отсутствуют, т.е. оператор умножения на t представляет собой пример оператора с чисто непрерывным спектром.
– регулярное для оператора А. Таким образом, спектр оператора А есть совокупность всех значений функции M(t) на отрезке [0;1], причем собственные значения отсутствуют, т.е. оператор умножения на t представляет собой пример оператора с чисто непрерывным спектром.
Замечания
Любой ограниченный линейный оператор, определенный в комплексном банаховом пространстве, имеющем хоты бы один отличный от нуля элемент, имеет непустой спектр. Существуют операторы, у которых спектр состоит из единственной точки (оператор умножения на число).
Теорема 5 может быть уточнена следующим образом. Пусть ![]() (можно доказать, что этот предел существует для любого ограниченного оператора А), тогда спектр оператора А целиком лежит внутри круга радиуса r с центром в нуле. Величина r называется спектральным радиусом оператора А.
(можно доказать, что этот предел существует для любого ограниченного оператора А), тогда спектр оператора А целиком лежит внутри круга радиуса r с центром в нуле. Величина r называется спектральным радиусом оператора А.
Резольвентные операторы ![]() и
и ![]() , отвечающие точкам
, отвечающие точкам ![]() и
и ![]() , перестановочны между собой и удовлетворяют соотношению
, перестановочны между собой и удовлетворяют соотношению ![]() , которое легко проверить, умножив обе части этого равенства на
, которое легко проверить, умножив обе части этого равенства на ![]() . Отсюда вытекает, что если
. Отсюда вытекает, что если ![]() – регулярная точка для А, то производная от
– регулярная точка для А, то производная от ![]() по
по ![]() при
при ![]() =
=![]() , т.е.
, т.е. 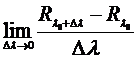 , существует (в смысле сходимости по операторной норме) и равна
, существует (в смысле сходимости по операторной норме) и равна ![]() .
.
§2. Унитарные операторы. Оператор сдвига
В этом разделе будем рассматривать пространство Н со скалярным произведением, которое является частным случаем нормированного пространства.
Похожие работы
... непрерывных и ограниченных функций – C[], заданный следующим образом: Af(x) = f(x+a). Функции f(x), f(x+a) C[], a R, f(x+a) – непрерывная и ограниченная функция. Покажем линейность оператора А, по определению 1 должны выполняться следующие аксиомы : 1) Аксиома аддитивности: А(f+g) = А(f) + А(g). А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g). По определению суммы функции, аксиома ...
... В этих формулах привлекательно то, что результат произведения двух операторов сдвигов выражается через операторы с действительными собственными значениями, как это следует из сопоставления правых частей уравнений (4.92) – (4.94), с одной стороны, и уравнений (4.90) и (4.91) – с другой. 4.3.5.13. Все коммутационные соотношения операторов момента импульса и его проекций, найденные в этом разделе,
... проектора Q пространства L на H, что tQ = Qt для любого вещественного s. (4). Найдем вид проектора. Положим e(x)=e . Тогда te=ee, а так как оператор Q линеен, то Qte = eQe. (5). Из (4) и (5) следует, что (Qe)(x-s) = e (Qe)(x). (6). Пусть С = (Qe)(0). При Q = 0 соотношение (6) имеет вид Qe = Ce. ...
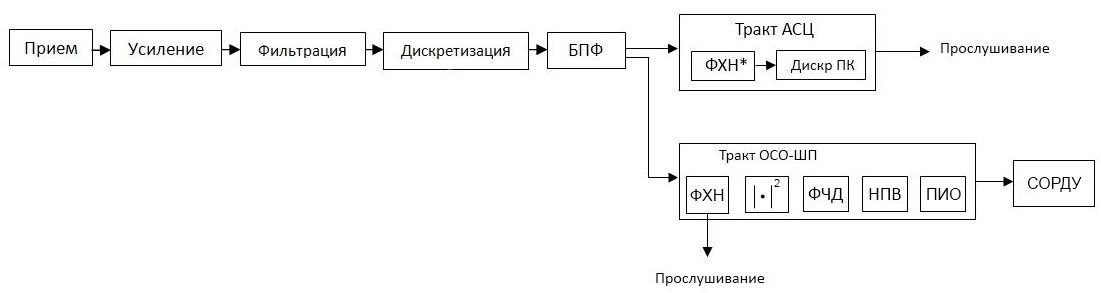
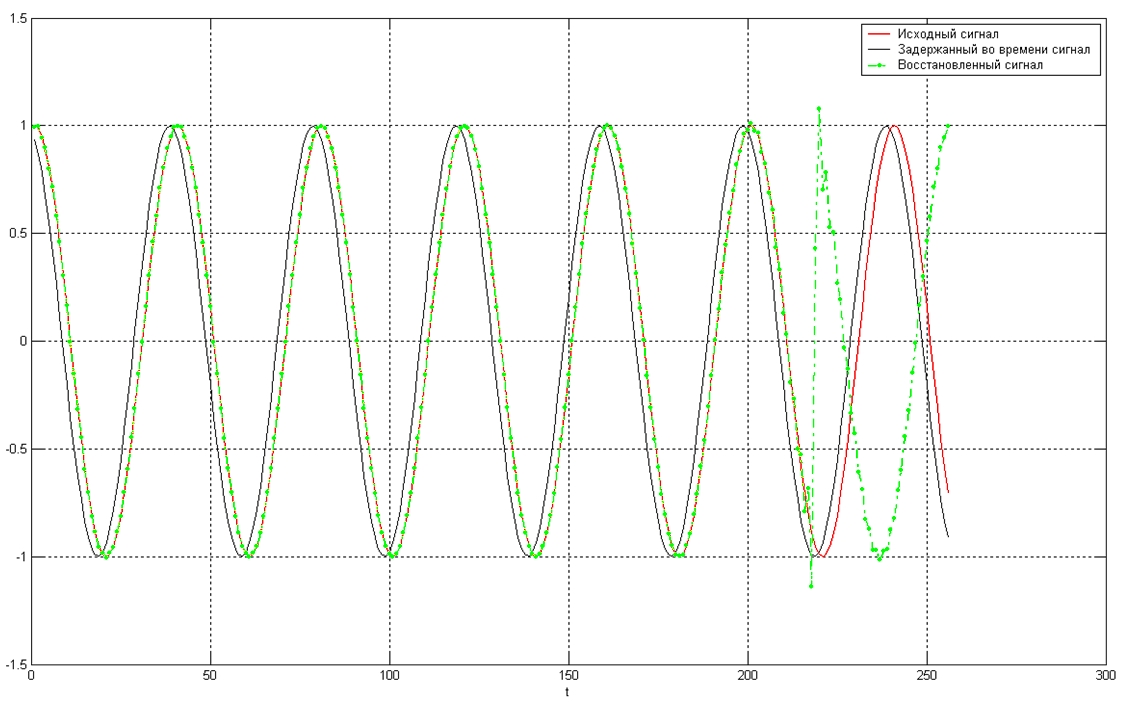
... частотного диапазона и внешний вид фильтра. То же самое мы видим и для других Частотных диапазонов на плакатах 2 и 3 . Доклад окончен Тема: Модель тракта прослушивания гидроакустических сигналов ОглавлениеВведение Место тракта прослушивания в структуре режима ШП типовой ГАС Формирование канала наблюдения в частотной области 3 Факторы, влияющие на восстановление сигнала 3.1 Перекрытие входных ...
0 комментариев