Навигация
Операторы сдвига в пространстве функции на единичной окружности
33462
знака
0
таблиц
0
изображений
8. Операторы сдвига в пространстве функции на единичной окружности
Рассмотрим единичную окружность на комплексной плоскости, т. е. всевозможные комплексные числа 
, по модулю равные 1. Рассмотрим комплексную последовательность 
и составим ряд 
. Если он сходится для всех , таких, что 
, то 
– функция от переменной 
, определенная на единичной окружности. Заметим, что для последовательностей из пространства 
, таких, что ряд 
сходящийся, ряд сходится для всех , таких, что . Итак, существует взаимно однозначное соответствие 
между пространством и множеством A функций на единичной окружности, представимых в виде суммы обобщенного степенного ряда с абсолютно сходящимся рядом коэффициентов. Рассмотрим, в какой оператор переходит при этом оператор сдвига U. Обозначим этот оператор 
. Пусть 
и 
– соответствующая функция. Тогда 
. Итак, в пространстве А оператору сдвига соответствует оператор умножения на функцию 
.
Рассмотрим теперь оператор 
взвешенного сдвига с весами 
. Его область определения – не все пространство , а только те последовательности 
, для которых сходится ряд 
. При этом
. Таким образом, в пространстве А оператору сдвига соответствует оператор дифференцирования.
Часть 2. Нестандартное расширение оператора сдвига
1. Нестандартное расширение поля действительных чисел
Поле R действительных чисел является расширением поля рациональных чисел с помощью определенной конструкции. Например, можно рассматривать действительные числа как классы фундаментальных последовательностей рациональных чисел.
Существует некоторая конструкция и для расширения поля R. При этом получается новое поле с линейным порядком, но без выполнения аксиомы Архимеда: 
. В новом поле существуют положительные элементы, меньшие любой дроби 
, где 
. Такие элементы называются бесконечно малыми. Также существуют положительные элементы, большие любого , они называются бесконечно большими. Это поле называется нестандартным расширением поля действительных чисел и обозначается *R.
Та же конструкция (которую мы не будем здесь описывать), дает расширение любого множества, построенного на основании поля действительных чисел, например, булеана 
, или прямого произведения 
. Поскольку отображение 
можно рассматривать как подмножество , то получаем также расширения всех числовых отображений. Всю полученную совокупность множеств называют нестандартным универсумом. На основании нестандартного универсума можно построить теорию, аналогичную математическому анализу, или нестандартный математический анализ.
Мы перечислим без доказательства некоторые необходимые в дальнейшем утверждения нестандартного анализа.
Принцип переноса
Если в стандартной теории верно некоторое утверждение, записанное логической формулой с конечным числом логических символов, то аналогичное утверждение верно и в нестандартном универсуме и наоборот.
Пусть дано бинарное отношение 
. Отношение называется направленным, если для любого конечного набора элементов 
существует элемент 
, который находится в отношении 
со всеми элементами данного набора.
Принцип направленности. Пусть дано направленное отношение . Тогда во множестве *В существует элемент 
, находящийся в отношении 
со всеми элементами множества А: 
Пример. Выведем из принципа направленности существование бесконечно большого числа в *R. Возьмем прямое произведение 
и на нем обычное отношение порядка: элементы x и y находятся в отношении , если 
. По принципу направленности: 
, что и означает, что в расширении 
существует элемент, который больше любого стандартного действительного числа, т. е. бесконечно большое число.
Теорема 10 [2]. Пусть 
- стандартная последовательность. Тогда . То есть число является пределом стандартной последовательности тогда и только тогда, когда для расширенной последовательности все члены с гипернатуральными номерами бесконечно близки к b.
(Соотношение , , означает, что – бесконечно малое число).
Доказательство.
1) Пусть , тогда по определению предела стандартной последовательности выполняется условие . Применим принцип переноса: . Но все бесконечно большие номера будут больше n0 , поэтому при любом стандартном положительном для любого бесконечного номера выполняется неравенство , что и означает .
Пусть . Возьмем стандартное ε>0 , тогда верно утверждение: . По принципу переноса такое же утверждение верно и в стандартном универсуме, следовательно, , что и требовалось доказать.
Множества, входящие в нестандартный универсум, называются внутренними. Это множества, которые являются элементами расширения булеана какого-то стандартного множества. Рассмотрим множества, являющиеся элементами , где – булеан . Для всех множеств из выполняется утверждение: если множество ограничено сверху, то оно имеет точную верхнюю грань (аксиома непрерывности). И определение ограниченности сверху, и определение точной нижней грани можно записать формулой с конечным числом символов, поэтому к данному утверждению применим принцип переноса. Значит, если множество ограничено сверху некоторым гипердействительным числом, то оно имеет точную верхнюю грань в , которую также будем обозначать .
Теорема 11. Пусть имеется внутреннее множество А
*R, причем . Тогда .
Доказательство. Очевидно, данное множество ограничено сверху, например, числом . Пусть М=sup А. Предположим от противного: пусть условие не выполняется, значит, положительное число не бесконечно малое. Значит, существует такое стандартное положительное число , что . Отсюда следует, что . А так как для любого число бесконечно малое, то , следовательно, М не является точной верхней гранью множества А, и предположение не верно.
2. Расширение пространств и
Рассмотрим следующие пространства:
1) l2 – пространство односторонних последовательностей комплексных чисел с натуральной нумерацией, для которых ряд 
- сходящийся.
2) l2(-∞;∞) – пространство двусторонних последовательностей комплексных чисел с нумерацией целыми числами, для которых соответственно ряд 
- сходящийся.
Соответственно, обозначим через *l2 нестандартное расширение пространства l2, которое также является линейным пространством над полем , наделенным скалярным произведением.
Определим, какие последовательности гиперкомплексных чисел будет содержать пространство *l2.
Так как по определению l2 ={{xi}/ C
R, nN: ≤ C}, то по принципу переноса
*l2={{xi}i*N / С*R, ν*N: ≤С} (*)
Т.е. в l2 входят гиперкомплексные последовательности с гипернатуральной нумерацией, удовлетворяющие условию (*). Аналогично, в *l2(-,) будут последовательности с гиперцелой нумерацией, члены которых также *С, удовлетворяющие аналогичному (*) условию
*-,)={{xi }/ С*R, ν: ≤С}.
Естественным образом в *l2 можно ввести норму: , но в отличие от нормы в l2, в *l2 норма может принимать также и бесконечные значения.
Докажем, что для расширений стандартных последовательностей .
Возьмем стандартную последовательность {xi}=x в пространстве l2 с нормой и любое стандартное . Воспользуемся теоремой 1: . Из этого утверждения следует, что верно следующее утверждение: , т.е. для любого стандартного число является верхней границей для множества всех сумм вида (1).
Обозначим М= (2)
Из предыдущего следует, что . С другой стороны, так как М , то ]. Но , значит, для любого стандартного , следовательно, М , или , что и требовалось доказать.
Похожие работы
... непрерывных и ограниченных функций – C[], заданный следующим образом: Af(x) = f(x+a). Функции f(x), f(x+a) C[], a R, f(x+a) – непрерывная и ограниченная функция. Покажем линейность оператора А, по определению 1 должны выполняться следующие аксиомы : 1) Аксиома аддитивности: А(f+g) = А(f) + А(g). А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g). По определению суммы функции, аксиома ...
... В этих формулах привлекательно то, что результат произведения двух операторов сдвигов выражается через операторы с действительными собственными значениями, как это следует из сопоставления правых частей уравнений (4.92) – (4.94), с одной стороны, и уравнений (4.90) и (4.91) – с другой. 4.3.5.13. Все коммутационные соотношения операторов момента импульса и его проекций, найденные в этом разделе,
... проектора Q пространства L на H, что tQ = Qt для любого вещественного s. (4). Найдем вид проектора. Положим e(x)=e . Тогда te=ee, а так как оператор Q линеен, то Qte = eQe. (5). Из (4) и (5) следует, что (Qe)(x-s) = e (Qe)(x). (6). Пусть С = (Qe)(0). При Q = 0 соотношение (6) имеет вид Qe = Ce. ...
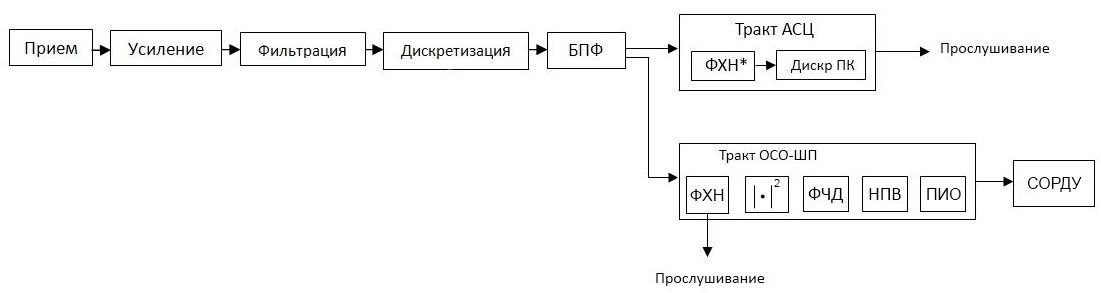
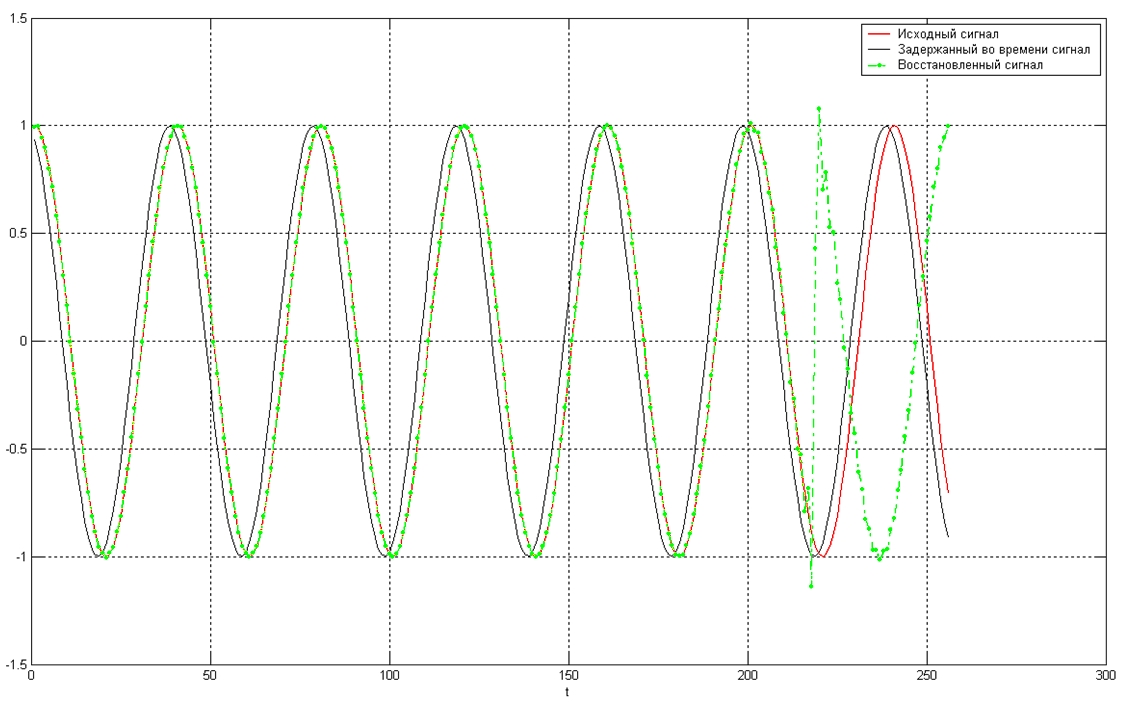
... частотного диапазона и внешний вид фильтра. То же самое мы видим и для других Частотных диапазонов на плакатах 2 и 3 . Доклад окончен Тема: Модель тракта прослушивания гидроакустических сигналов ОглавлениеВведение Место тракта прослушивания в структуре режима ШП типовой ГАС Формирование канала наблюдения в частотной области 3 Факторы, влияющие на восстановление сигнала 3.1 Перекрытие входных ...
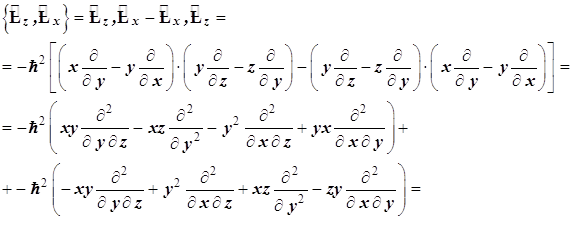
0 комментариев