Навигация
Операторы сдвига в нестандартном расширении пространства последовательностей
33462
знака
0
таблиц
0
изображений
3. Операторы сдвига в нестандартном расширении пространства последовательностей
В дальнейшем Н – гильбертово пространство, 
– пространство всех линейных ограниченных операторов в Н.
Для линейных операторов в нестандартных пространствах можно ввести аналоги основных понятий теории операторов: ограниченности, нормы, спектра. При этом можно рассматривать различные пространства операторов: например, – множество всех расширений операторов из пространства ; – множество всех линейных операторов , имеющих конечную норму, т. е. удовлетворяющих условию ; *(L(H)) – расширение пространства всех линейных ограниченных операторов в Н.
Мы будем рассматривать операторы из пространства *(L(H)). Для операторов из этого пространства можно ввести норму как расширение нормы на пространстве *(L(H)). Но в отличие от стандартной нормы она может быть также и бесконечна. Назовем оператор из *(L(H)) ограниченным, если его норма конечна
Определение 13. Спектром оператора А*(L(H)) называется множество точек λ, для которых оператор А– λI не имеет ограниченного обратного в *(L(H)).
Теорема 12. Если существует элемент с не бесконечно малой нормой, такой, что для некоторого λ, то число 
принадлежит спектру оператора А.
Доказательство. Предположим, что обратный оператор существует. Обозначим . Тогда , а . Норма элемента равна 1, а норма элемента бесконечно большая. Отсюда следует, что оператор не ограничен.
Определение 14. Элемент с не бесконечно малой нормой, такой, что для некоторого λ, называется почти собственным вектором оператора А, а число – точкой почти собственного спектра оператора А.
Рассмотрим оператор сдвига U в пространстве , т. е. оператор, каждую последовательность вида переводящий в последовательность вида
Также будем рассматривать оператор двустороннего сдвига , он каждую последовательность вида сдвигает вправо, т.е. переводит в последовательность .
Рассмотрим следующую задачу. В пространстве * возьмем следующую последовательность: , где – бесконечно большой номер. Найдем норму этого элемента: . Если же качестве возьмем , то получим . Покажем, что данный элемент является почти собственным вектором оператора сдвига с почти собственным числом , т. е. . Действительно, =, следовательно, .
Можно доказать также более общий факт.
Теорема 13. Любая точка единичной окружности является почти собственным числом оператора двухстороннего сдвига, соответствующим некоторому почти собственному вектору.
Доказательство. В пространстве *l2(-,) рассмотрим следующую последовательность: 
=, где = и – некоторый бесконечно большой номер. Найдем норму этого элемента: . Возьмем и рассмотрим разность . Так как
Ux=, ,
то . Найдем норму этой разности: , т. е. .
Заключение
В работе показано, что нестандартное расширение оператора сдвига сохраняет многие свойства стандартного сдвига, в частности, свойство ограниченности и норму. Но также имеются и отличия, например, существование у нестандартного оператора сдвига почти собственных векторов.
Список литературыГельфанд И.М. Лекции по линейной алгебре.–М.: Мир, 1964.
Девис Д. Прикладной нестандартный анализ.
Колмогоров А.Н. Элементы теории функций и функционального анализа [Текст]./ А.Н. Колмогоров, С.В. Фомин. – М.: Просвещение, 1968.
Халмош П. Гильбертово пространство в задачах [Текст]. – М.: Просвещение, 19
Похожие работы
... непрерывных и ограниченных функций – C[], заданный следующим образом: Af(x) = f(x+a). Функции f(x), f(x+a) C[], a R, f(x+a) – непрерывная и ограниченная функция. Покажем линейность оператора А, по определению 1 должны выполняться следующие аксиомы : 1) Аксиома аддитивности: А(f+g) = А(f) + А(g). А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g). По определению суммы функции, аксиома ...
... В этих формулах привлекательно то, что результат произведения двух операторов сдвигов выражается через операторы с действительными собственными значениями, как это следует из сопоставления правых частей уравнений (4.92) – (4.94), с одной стороны, и уравнений (4.90) и (4.91) – с другой. 4.3.5.13. Все коммутационные соотношения операторов момента импульса и его проекций, найденные в этом разделе,
... проектора Q пространства L на H, что tQ = Qt для любого вещественного s. (4). Найдем вид проектора. Положим e(x)=e . Тогда te=ee, а так как оператор Q линеен, то Qte = eQe. (5). Из (4) и (5) следует, что (Qe)(x-s) = e (Qe)(x). (6). Пусть С = (Qe)(0). При Q = 0 соотношение (6) имеет вид Qe = Ce. ...
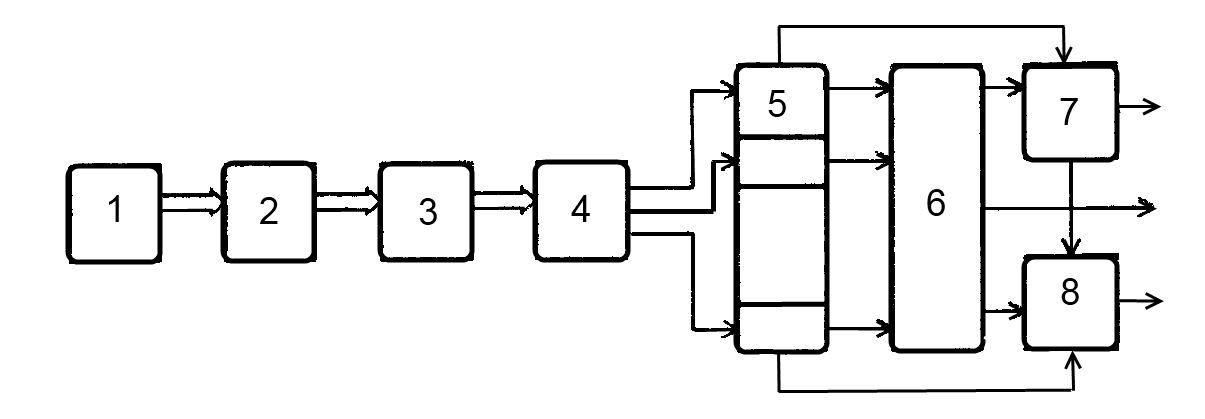
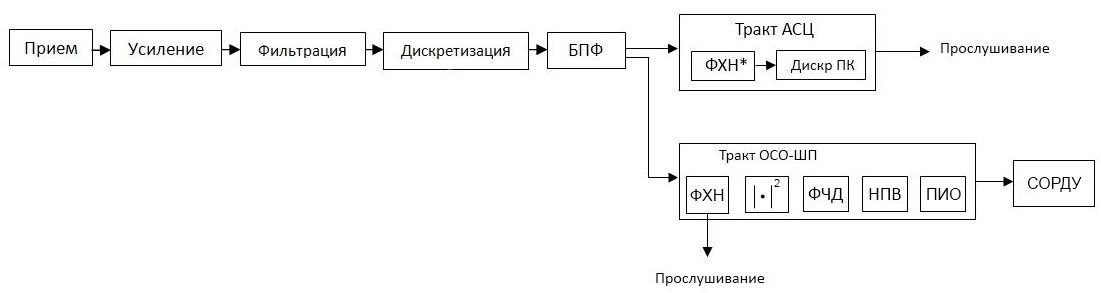
... частотного диапазона и внешний вид фильтра. То же самое мы видим и для других Частотных диапазонов на плакатах 2 и 3 . Доклад окончен Тема: Модель тракта прослушивания гидроакустических сигналов ОглавлениеВведение Место тракта прослушивания в структуре режима ШП типовой ГАС Формирование канала наблюдения в частотной области 3 Факторы, влияющие на восстановление сигнала 3.1 Перекрытие входных ...
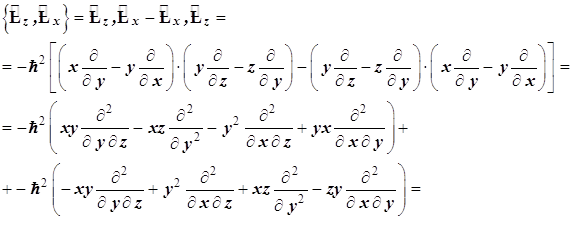
0 комментариев