Навигация
Ограниченность и норма линейного оператора
33462
знака
0
таблиц
0
изображений
2. Ограниченность и норма линейного оператора
Определение 2. Линейный оператор, действующий из Е в Е1, называется ограниченным, если он определен на всем Е и каждое ограниченное множество переводит снова в ограниченное. Между непрерывностью и ограниченностью линейного оператора существует тесная связь, т.е. справедливы следующие утверждения:
Теорема 1. Для того, чтобы линейный оператор 
был непрерывным, необходимо и достаточно, чтобы он был ограничен.
1. Пусть оператор А неограничен. Тогда существует М
Е – ограниченное множество, такое, что множество АМЕ1 не ограничено. Следовательно, в Е1 найдется такая окрестность нуля V, что ни одно из множеств 
АМ не содержится в V. Но тогда существует такая последовательность хn
M , что ни один из элементов Ахn не принадлежит V и получаем, что 
в Е, но 
не сходится к 0 в Е; это противоречит непрерывности оператора А.
2. Если оператор А не непрерывен в точке 0, то в Е1 существует такая последовательность 
, что Ахn не стремится к 0. При этом последовательность 
ограничена, а последовательность 
не ограничена. Итак, если оператор А не непрерывен, то А и не ограничен. Утверждение доказано.
Если Е и Е1 – нормированные пространства, то условие ограниченности оператора А, действующего из Е в Е1, можно сформулировать так: оператор А называется ограниченным, если он переводит любой шар в ограниченное множество.
В силу линейности оператора А это условие можно сформулировать так: оператор А ограничен, если существует С=const , что для любого 
Е : 
.
Определение 3. Наименьшее из чисел С, удовлетворяющих этому неравенству, называется нормой оператора А и обозначается 
.
Теорема 2 [1]. Для любого ограниченного оператора А , действующего из нормированного пространства в нормированное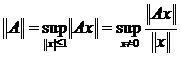 
.
3. Сумма и произведение линейных операторов. Пространство линейных непрерывных операторов
Определение 4. Пусть А и В – два линейных оператора, действующих из линейного топологического пространства Е в пространство Е1. Назовем их суммой А+В оператор С, ставящий в соответствие элементу 
элемент у=Ах+Вх, 
.
Можно проверить, что С=А+В – линейный оператор, непрерывный, если А и В непрерывны. Область определения DC оператора С есть пересечение 
областей определения операторов А и В.
Если Е и Е1 – нормированные пространства, а операторы А и В ограничены, то С тоже ограничен, причем
(2)
Действительно, для любых х 
, следовательно, выполняется неравенство (2).
Определение 5. Пусть А и В – линейные операторы, причем А действует из Е в Е1, а В действует из Е1 в Е2 . Произведением ВА операторов А и В называется оператор С, ставящий в соответствие элементу 
элемент 
из Е2.
Область определения DC оператора С=ВА состоит из тех хDA , для которых АхDB. Ясно , что оператор С линеен. Он непрерывен, если А и В непрерывны.
Если А и В – ограниченные операторы, действующие в нормированных пространствах, то и оператор С=ВА – ограничен, причем
(3)
Действительно, 
, следовательно, выполняется (3).
Сумма и произведение трех и более операторов определяются последовательно. Обе эти операции ассоциативны.
Произведение оператора А на число к (обозначается кА) определяется как оператор, который элементу х ставит в соответствие элемент кАх.
Совокупность Z(E,E1) всех непрерывных линейных операторов, определенных на всем Е и отображающих Е в Е1 ( где Е и Е1
– фиксированные линейные нормированные пространства), образует, по отношению к введенным операциям сложения и умножения на число, линейное пространство. При этом Z(E, E1) – нормированное пространстово (с тем определением нормы оператора, которое было дано выше).
Похожие работы
... непрерывных и ограниченных функций – C[], заданный следующим образом: Af(x) = f(x+a). Функции f(x), f(x+a) C[], a R, f(x+a) – непрерывная и ограниченная функция. Покажем линейность оператора А, по определению 1 должны выполняться следующие аксиомы : 1) Аксиома аддитивности: А(f+g) = А(f) + А(g). А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g). По определению суммы функции, аксиома ...
... В этих формулах привлекательно то, что результат произведения двух операторов сдвигов выражается через операторы с действительными собственными значениями, как это следует из сопоставления правых частей уравнений (4.92) – (4.94), с одной стороны, и уравнений (4.90) и (4.91) – с другой. 4.3.5.13. Все коммутационные соотношения операторов момента импульса и его проекций, найденные в этом разделе,
... проектора Q пространства L на H, что tQ = Qt для любого вещественного s. (4). Найдем вид проектора. Положим e(x)=e . Тогда te=ee, а так как оператор Q линеен, то Qte = eQe. (5). Из (4) и (5) следует, что (Qe)(x-s) = e (Qe)(x). (6). Пусть С = (Qe)(0). При Q = 0 соотношение (6) имеет вид Qe = Ce. ...
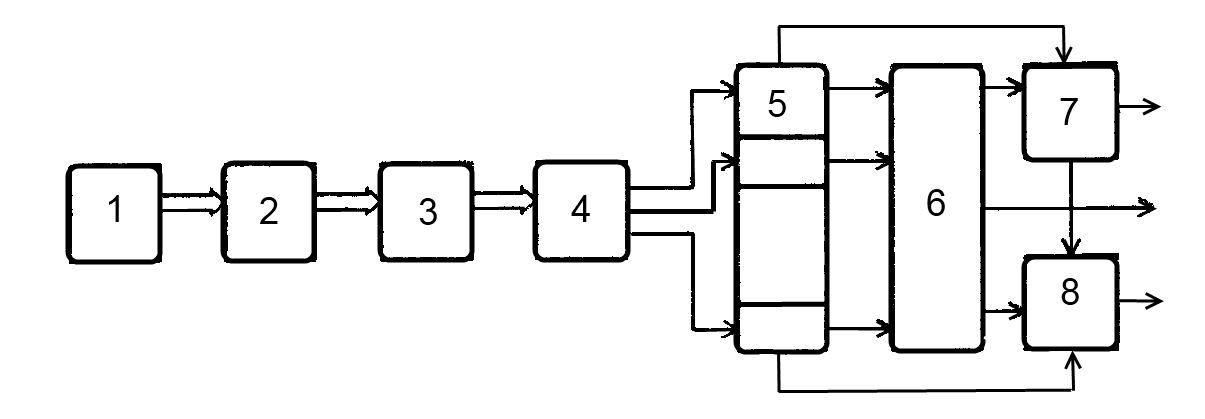
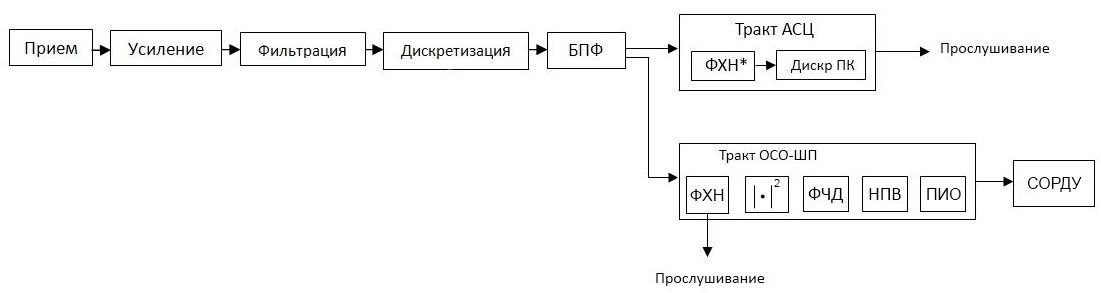
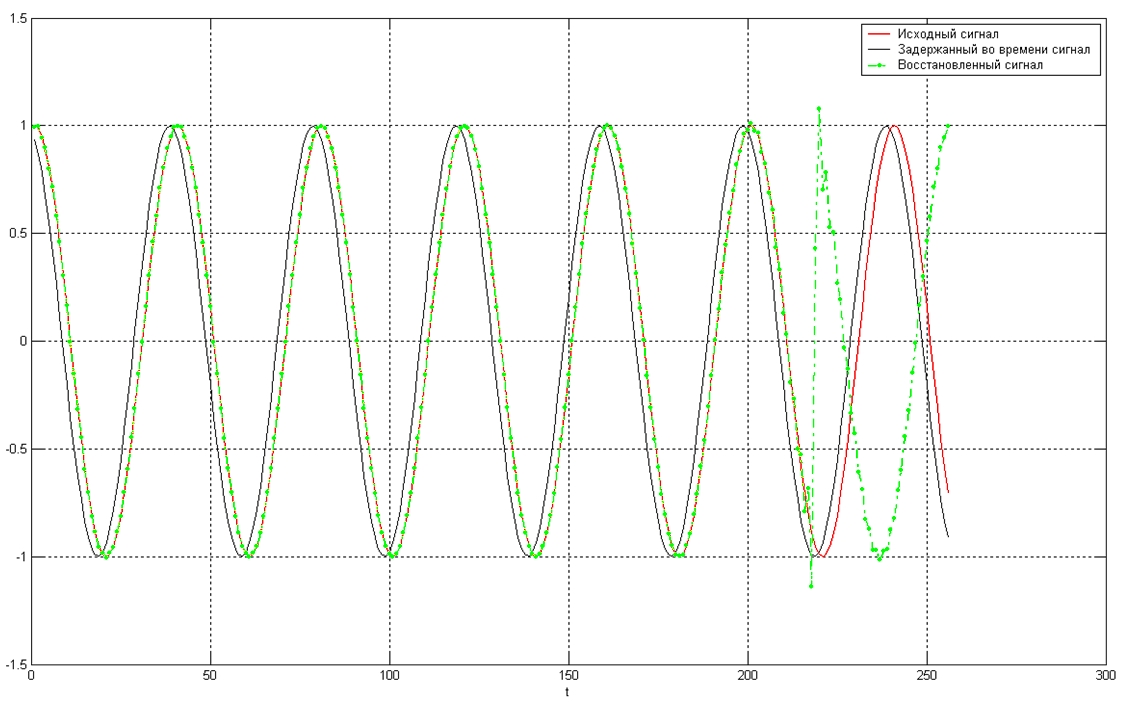
... частотного диапазона и внешний вид фильтра. То же самое мы видим и для других Частотных диапазонов на плакатах 2 и 3 . Доклад окончен Тема: Модель тракта прослушивания гидроакустических сигналов ОглавлениеВведение Место тракта прослушивания в структуре режима ШП типовой ГАС Формирование канала наблюдения в частотной области 3 Факторы, влияющие на восстановление сигнала 3.1 Перекрытие входных ...
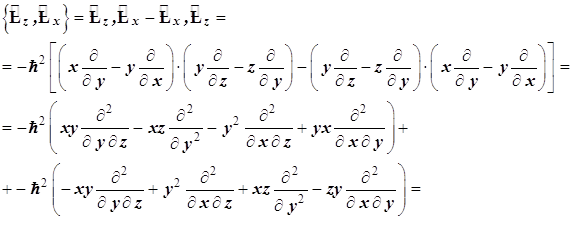
0 комментариев