Навигация
20 а ~в Þ аM в, вM аÞ в ~а.
30 а ~в, в~с Þ аM в, вM с Þ аM с Þ c~a Þ a ~c
вM a, сM в Þ сM в ,в M а Þ сM а
Вопрос 7 Гомоморфизм колец
В вопросе ставиться проблема взаимосвязи алгебр на примере колец, которые описываются гомоморфизмом. Предлогаеться решить проблему взаимосвязи кольца, фактор-кольца с другим кольцом, которая задаётся теоремой об эпиморфизме колец. Предварительно введём ряд понятий. Прежде всего, сформулируем определение алгебры и гомоморфизма алгебры.
| Опр.1 | Алгеброй называется упорядоченное множество двух множеств <A,U>, где А |
множество элементов любой природы, а U-множество операций.
Для введения определения кольца необходимо рассмотреть непустое множество и задание операций.
| Опр.2 | Гомоморфизмом алгебр называется отображение одной из них в другое, сохра - |
няющее операции, т.е. если А , В – алгебры , с U, W – множествами опреаций, f – гомоморфизм А в В , то ![]() ▲
▲![]() U, существует ■
U, существует ■ ![]() W.
W.
Гомоморфизм алгебр допускает классификацию:
| Свойства f | Гомоморфизм | Мономорфизм | Эпиморфизм | Изоморфизм |
| 1.Сохранение операций | ||||
| 2.x1 | ||||
| | ||||
| Все св-ва 1 - 3 |
Сформулировать определения мономорфизма, эпиморфизма, изоморфизма предоставляется читателю.
Рассмотрим гомоморфизм колец.
| Опр.3 | Гомоморфизмом кольца <K, +, |
Сохраняющее операции, т.е. f(а+в)=f(а)Å f(в) ; f(ав)=f(а)Ä f(в).
| Опр.4 | Ядром гомоморфизма f: |
которых равны нулю кольца К, т.е. Ker f =![]()
| Теорема 5 | Ker f кольца К в |
f(a-в)=f(а+(-в))=f(а)+f(-в)=f(а)-f(в)=0¢ - 0¢ =0¢ Î K Þ а-в Î Ker f
f(ак)=f(а) f(к)=0¢ f(к)=0¢ Πʢ Þ àêÎ Ker f
f(ка)=f(к) f(а)= f(к) 0¢ =0¢ Πʢ Þ êàÎ Ker f ,что и доказывает, что Ker f кольцо К в К ¢ является идеалом К
Имея К и идеал его I , можно задать отношение сравнения по идеалу. Известно, что это отношение является эквивалентностью поэтому задано разбиение, а следовательно, фоктор - кольца. Рассмотрим отображение Е : К® К /I, где Е(x)=Kx
Покажем что Е – гомоморфизм ( эпиморфизм ).
E(x+y)=Kx+y=Kx+Ky=E(x)+E(y); E(xy)=Kxy=KxKy=E(x)E(y).
" Kx Î K / I ;$ xÎ K, E(x)=Kx . Это позволяет утверждать что Е - эпиморфизм .
| Теорема 6 | Если f: K® K¢ эпиморфизм, то существует изоморфизм K / Ker f на K¢ такой, |
что эпиморфизм f равен композиции Е и изоморфизма.
Для доказательства теоремы предварительно рассмотрим и зафиксируем условие теоремы.К, К¢ - кольца , f: K® K¢ , f(x)=x¢ -эпиморфизм, тогда f обладает ядром Kerf, которое является идеалом K. Становиться возможным К фиксировать по Ker f = I, получаем фактор –кольцо К / Ker f. Рассмотрим Е: К® Ker f, где E(x)=Kx –эпиморфизм. Теперь можно приступать к доказательству теоремы, которое предполагает выполнение процедур по плану:
покажем что для x,yÎ Kx , f(x)=f(y), зададим отображение Y : K/Ker f ® K¢ так :Y (Kx)=f(x), проверим, что Y - гомоморфизм,Y - эпиморфизм,
Y - мономорфизм.
f = Y ° E.Итак, покажем, что для x,yÎ Kx, f(x)=f(y). Пусть f(x)¹ f(y) Þ f(x)-f(y)¹ 0¢ Þ f(x-y)¹ 0¢ ® x-y Ï Ker f Þ x ![]() y(mod Ker f)
y(mod Ker f)![]() Þ xÏ Kx Ú yÏ Ky ,что противоречит
Þ xÏ Kx Ú yÏ Ky ,что противоречит
условию. Поэтому утверждение верно. Изобразим условие теоремы и результат доказанного схемой
K
· x f f(x) K¢
· y
Y
Ker f 0¢
E Kx
0¢ ¢ K¤ Ker f
![]()
Зададим отображение Y : К/ker f® K’ , Y (Kx)=f(x).
Y (Kx+Ky)=Y (Kx+y)=f(x+y)=f(x)+f(y)=Y (Kx)+Y (Ky);
Y (KxKy)=Y (Kxy)=f(xy)=f(x)f(y)=Y (Kx)Y (Ky), т. е. Y -гомоморфизм.
Кх¹ КуÞ Y (Кх)¹ Y (Ку).Пусть это не так, пусть Y (Кх)=Y (Ку)Þ f(х)=f(у)Þ х и у из одного класса,что противоречит условию; т.е.Y - мономорфизм. х¢ Î К¢ ; т.к. f- эпиморфизм, то$ хÎ К, f(х)=х¢ , тогда $ Кх Î К(ker f : E(х)=Кх, а Y (Кх)=х¢ , что позволяет утвердждать: Y - эпиморфизм
Итак , Y -изоморфизм К/ker f и К¢ .
Пусть Y оЕ(х) ;Y оЕ(х)=Y (Е(х))=Y (Кх)=f(х)Þ Y оЕ=f
Вопрос 8 . Делимость в кольце целых чисел (Z )
В вопросе ставится проблема отношения делимости в кольце целых чисел и возможное его приложение для нахождения НОД и НОК целых чисел.
Опр.1.
Число а Î Z называется делящимся на число в¹ оÎ Z , если существует такое число с, что а=вс,
а называют в этом случае делимым, в – делителем, с – частным. Обозначают отношение ² ![]() ”.
”.
Отношение делимости на Z обладает рядом свойств:
1° " а¹ 0, аM а, | Доказательство:
2° " а¹ 0, в¹ 0, а:M в, вM аÞ а=в, | а¹ 0 Þ а=а× 1Þ аM а;
3° " а,в,с, а:в и вM сÞ аM с | аM вÞ а=вс
Истинность названных трех | вM аÞ в=аd } Þ а=а(dс)Þ а× 1=а(dс)Þ
Свойств позволяют утверждать, | а(1-dс)=0Þ 1-dс=0Þ dс=1 (нет делителей редко)Þ
Что отношение делимости |d и с делением 1, т.е.равны 1 или (-1)
является нестрогим частичным | аM вÞ а=вк } Þ а=с(mк)Þ аM с
порядком. | вM сÞ в=сm}
4° а:в ,сM вÞ а+вM с, авM с
5° асM вс, с¹ 0Þ аM в и ряд других
Убедимся в том, что отношение делимости не обладает свойством связности , т.е. является частичным. Это легко проверить примером: 4: /5. Потому естественным образом возникает проблема деления целого числа на другое не равное нулю. Такая ситуация описывается теоремой о делении с остатком.
Т 2.
" а,в¹ 0, Z (!)gч такие, что а=вg+ч, где 0£ ч< в
Теорема содержит в себе две: о существовании и о единств.
Рассмотрим ихдоказательства.
Случай 1. а³ 0.Проведем доказательство методом матиндукции.
а=0 Þ 0=в0+0, где видно , что g=0, r=0Î Z
а=п Þ и пусть теорема для п верна, т.е.
(1) п=вg+r, 0£ r , 0< в
а=п+1Þ прибавим к обеим частям равенства (1) по 1, получим:
п+1=вg+(r+1). Исследуем (r+1).Если r+1< в, то теорема верна для п+1, если r+1=в,то
п+1=в(g+1)+0 и теорема вновь верна. На основании принципа матиндукции можно утверждать,что теорема верна для любого целого числа а³ 0.
Случай 2. а< 0, тогда -а> 0 и теорема для этого числа верна, т.е.-а=вg+r 0Þ r< в.
Поступим так:
А=в(-g)+(-r), прибавим к левой части и вычтем в, получим а=в(-g)-в+в+(-r)Þ a=b(-1-g)+
(b-r), где –1-gÎ Z , в-r < в, при r> 0, т.е. теорема верна.
(!) Пусть для а,в> 0Î Z существует два варианта:
а=вg1+r1, а=вg2+r2, где 0£ r1,r2< в.
Заметим, что g1=g2Û r1=r2.
Действительно, если r1=r2Þ r1-r2=в(g2-g1)=0, в¹ 0Þ g2-g1=0Þ
G1=g2, g1=g2Þ g2-g1=0Þ r1-r2=0Þ r1=r2.
Поэтому рассмотрим случай, когда r1¹ r2, тогда вg1+r1=вg2+r2Þ r1-r2=в(g2-g1).
Так как 0 £ r£ b, 0£ r2< b, то r1-r2< b. С другой стороны ê b(g2-g1)ê = ê bê ê g2-g1ê > g1¹ g2> b,
Т.е. R1-r2> b, что привело к противоречнию. Теорема доказана.
Рассмотрим возможное применение отношения делимости и отношения с остатком для введения
и способа вычисления НОД и НОК двух целых (натуральных) чисел. Введем определение
НОД и НОК.
Опр.3 Наибольшим общим делителем двух целых чисел а и в называется такой
Их общий делитель, который делится на всякий другой их общий делитель.
Опр.4. Наименьшим общим кратным двух целых чисел называется такое их
общее кратное , на которое делится всякое другое их общее кратное.
НОД и НОК двух чисел и большего числа можно находить способом разложения на
простые множители. Здесь рассмотрим другие способы в частности, алгоритм
Евклида.
Алгоритм Евклида представляет собой конечный процесс деления одного числа
на другое, затем второго числа на первый остаток, затем первый остаток
деления на второй и так до тех пор, пока деление завершится без остатков.
Это считается возможным, потому что остатки будут неотрицательным числом,
убывают, что бесконечным быть не может.
Оформим этот процесс математически:
а= bg1+r1, 0< r1< b,
b=r1g2+r2, 0 < r2< r1,
…………..
rk-2=rk-1gk+rk, 0< rk< rk-1
rk-1=rkgk+1 rk+1=0
и докажем теорему о нахождении НОД чисел. Заметим, что НОД чисел обозначаем так:
НОД (а;в), или просто (а,в)
Теорема 5
Последний, отличный от нуля, остаток в алгебре Евклида является НОД (а;в).
Для доказательства требуется предварительно рассмотреть две леммы:
Лемма 1: а=вg+r, то (а,в)=(в,r)
(a,b)=d® aM d1bM dÞ a-bgM dÞ rM dÞ d – общий делитель в и r,
т.е., если (в,r)=d1,то d1M d (1)
(в,r)=d1® bM d1, rM d1Þ aM d1Þ d1общий делитель a и b,Þ dM d1 (2)
Из (1) и (2) следует, что d=d1
Лемма 2: аM вÞ (а,в)=в
Теперь допишем теорему. Из последнего равенства в алгоритме Евклида следует, что
(rk-1,rk)=rk. А из предпоследнего, по лемме, следует, что (rk-2,rk-1)=(rk-1,rk)=rk
Поднимаясь от равенства к равенству в алгоритме Евклида получим (а,в)=,rk
Что и требовалось доказать.
Решим вопрос о нахождении НОК (а,в).Обозначим НОК (а,в)=m
И докажем теорему
Теорема 6 m=ab/(a,d). Для доказетельства воспользуемся определением НОК.
Напишем, что ав/(а,в) делится на а и на в.
(а,в)=Þ a=a1d, тогда ab/(ab)=a1db1d/d(a1b1)=ab1=a1b, что и доказывает утверждение.
………..b=b1d
………..(a1,b1)=1
Покажем, что любое кратное чисел а и в делится на m.Пусть М общее кратное а и вÞ
М=ак, М=вmÞ M=abs=absd/d=ab/(a,b)sdÞ
M:ab/(a,b), что и требовалось доказать. Используя определение НОК (а,в) можно
Сделать вывод, что m=ab/(a1b)
Вопрос 9 Элементы теории сравнения с кольце Z
В вопросе решается проблемы возможности задания бинарного отношения
”cравнение по модулю m” в кольце целых чисел, его свойств, среди которых построение
новых алгебр из Z .
Пусть Z -кольцо целых чисел, m Î Z , m > 1
Опр.1 Числа а и в называются сравнимыми по модулю m, если а-в:m.
Записывается: а=в(modm).
Легко показать, что введенное бинарное отношение на Z является отношением эквивалентности, т.е.
обладает свойствами рефлексивности ,симметричности ,транзитивности.
Действительно:
1° a-a=0Î Z , 0:mÞ aº a (modm);
2° aº b (modm)Þ a-b:mÞ b-a:mÞ bº a (modm);
3° aº b (modm), bº c (modm)Þ a-b:m,Þ (a-b)+(b-c):mÞ a-c:mÞ
…………………………………aº c (modm)
Это очень важное свойство отношения сравнения,т.к. в таком случае оно задает разбиение
На Z , что рождает фактор – множество К/m=Z m, как множество классов эквивалентности.
Общая теория колец рассматривает эту ситуацию и утверждает, что<Z m,+,x> - кольцо.
Здесь же мы рассмотрим порождение другой алгебры – мультипликативной группы.
Для этого введем понятие взаимной простоты класса и модулем m.
Класс Ка=а называется взаимнопростым с m, если (а,m)=1, где а –образующей класса Ка
Однако в теории классов известно, что таким обьразующим может быть любой элемент из этого
класса).
Рассмотрим множество классов вычетов, каждый из которых взаимно прост с m.
Известно, что количество чисел, взаимно простых с модулем определяет функцию
Эйлера g(m) ,и что остатком от деления целых чисел на m составляют полную систему вычетов
Взаимно простые с m следует искать среди классов Ко,К1,К2,…,Кm-1. Пусть такими
классами будут í r1,r2,…rg(m) ý . Такую систему классов называют приведенной
Системой классов вычетов и их представителем приведенной системы вычестов
í r1,r2,…rg(m)ý .
В этой системе ровно g(m) элементов, ( ri,m)=1, (ri,m)=1
Теперь докажем теорему о приведенной системе классов вычетов.
Теорема 2. Приведенная система классов вычетов по модулю не образует
мультипликативную группу.
Для доказательства теоремы необходимо проверить существенные признаки мультипликативной группы,
т.е. проверить:
замкнутость относительного умножения, ассоциативность умножения, существование единичного элемента, существование для каждого элемента обратного.Рассмотрим { r1,ri,…rg(m)} ,где (ri,m)=1, напомним ,что ri× rj=ri× rj.
(rim)=1Þ
(rj,m)=1
(ri,m)=1……(rj,m)=1 Если предположить, что (ri× rj,m)¹ 1, то это будет означать, что
най р-простое число такое, что ri× rj:p1Þ m:p
Если ri или rj делятся на р, то нарушаем условие (1).Если ri p, то по известному утверждению,
² a× b:p,(a,p)=1Þ b:p² , следует, ri:p, что также приводит к противоречию (1). И так,
(ri:rj,p)=1Þ
(ri× rj,p)=1, т.е.rirgÎ { r1,r2,…rj(m)} , что утверждает с необходимостью замкнутость
очередного умножения. Так как классы вычетов riÎ Z m, то умножение
Так как (1,m)=1, то ri=1, т.е. единый класс в рассматриваемом множестве есть.
Пусть аÎ Z , (а,m)=1, рассмотрим{ ar1,ar2,…arg(m)} .Легко показать, что
Это тоже приведенная система вычетов.Тогда ari=1Þ a× ri=1, т.е. для ri
Существует класс ему обратный: а=ri-1. Можно существование обратного класса доказать и таким
Способом: a,r2…rg(m)=rj, сократим на ri, получим r1,r2…rj-1,rj+1 rg(m)=1, тогда
(r2…rg(m)=(r1)-1,(r1r3…rg(m)=(r2)-2 и т.д., что подвтерждает факт существования для
каждого класса ri ему обращенного ri-1. Теорема доказана.
Теория сравнения имеет всевозможное применение. В частности, теория сравнения
Используется при выводе признаков делимости. Сформулируем общий признак
Делимости на mÎ Z , m> 1, который назван признаком Паскаля. В основе этого признака лежит систематическая запись натурального числа в системе с основанием g, т.е.
(anan-1…a1a0)g=an× gn+an-1gn-1+…a1g1+a0g° .
Теорема 3.(Паскаля) Число а=(аn,an-1…a1,a0)g делится на mÎ Z ,m> 1 тогда и только
Тогда, когда на m деления в число: anrm+an-1rn-1+…a1r1+a0r0, где ri остаток
От деления gi на m.
g° =mg0+r0, g1=mg2+r1,…gn=mgn=rnÞ
g0º r0(m0dm),g1º r1(m0d0),…,gnº rn(m0d0). Используя свойства сравнения легко получаем,
что angn+…+a0g0º anrn+…+a0r0 (m0d0). Воспользуемся определение сравнения, мы получаем истинность теоремы.
Общий признак позволяет вывести частный признак.
Выведем признак делимости на 3 и на 5, если число записано в десятичной
Системе исчисления.
m=3, g=10,тогда 10° =1º 1(mod3),10º 1 (mod3), используем лемму, можно утверждать, что остатки ri =1, по
по признаку Паскаля
(anan-1…a0)10º an+…a0(mod3), откуда можно сфоормулировать признак
делимости на 3:
“Число делится на 3 тогда и только тогда, когла сумма его цифр в
десятичной делится на 3”.
Пусть b Î Р(a ), т.к. Р(a ) = Р[ a ] , то b = аSa s +···+a1a + a0, где f(х) = аSхs +···+a1х + a0Î Р[ х] , f(a ) = b . Пусть g(х) – линейный элемент для a , т.е. g(х) = bnхn + ···+ b1х + b0. Разделим f(х) на g(х) :
f(х) = g(х) g1(х) + r(х), 0£ deg r(х) < n, т.е. r(х) = с0 + с1х +···+ сn-1хn-1. (сiÎ р).положим х = a в (1), получим f(a ) = g(a ) g1(a ) + r(a ), т.к. g(a ) = 0, то f(a ) = r(a ), т.е. b = с0 + с1a +···+ сn-1a n-1. Получили, что такое представление однозначное.
Пусть b = с0 + с1a +···+ сn-1a n-1 и b = d0 + d1a +···+ dn-1a n-1.
Рассмотрим многочлен φ(х) = (с0 - d0) + (с1 - d1)х + ∙∙∙ + (сn-1 - dn-1)х n-1, причем φ(a ) = 0, т.е. получился многочлен, степени меньше чем n, для которого a является корнем, что противеречит линейности многочлена для a . Если φ(х) существует, то он нулевой, поэтому сi = di, что и доказывает теорему.
Посмотрим как возможно изменить эту теорему для освобождения от алгебраической иррациональности в знаменатели дроби.
Пусть a – алгебраический элемент степени n > 1 не из Р
Пусть f(х), h(х) два многочлена из Р[ х] , h(a ) ¹ 0. Тогда в р(a ) может быть дробь ![]() . Возникает проблема представить дробь в виде линейной комбинации
. Возникает проблема представить дробь в виде линейной комбинации
степеней a . Это возможно, так как любой элемент из р(a ) есть линейная комбинация 1, a ,…,a n-1 Задача состоит в нахождении алгоритма преобразования.
Пусть g(х) – минимальный многочлен для a степени n. Т.к. h(a ) ¹ 0, то h(х)![]() g(х) ® (h(х), g(х)) = 1 = > uh + vg = 1. Т.к. g(a ) = 0, u (a ) h (a ) = 1 u(a ) =
g(х) ® (h(х), g(х)) = 1 = > uh + vg = 1. Т.к. g(a ) = 0, u (a ) h (a ) = 1 u(a ) = ![]() . Следовательно,
. Следовательно, ![]() = f (a )u(a ) , где f(х), u(х) Î Р[ х] , а f (a ), u(a )Î Р[ a ] . Таким образом удалось освободиться от иррациональности в знаменателе дроби, а сделать это можно так:
= f (a )u(a ) , где f(х), u(х) Î Р[ х] , а f (a ), u(a )Î Р[ a ] . Таким образом удалось освободиться от иррациональности в знаменателе дроби, а сделать это можно так:
![]() = f (a )u(a )
= f (a )u(a )
Вопрос 10. Кольцо многочленов от одной переменной.
Вопрос предполагает решение проблемы построения кольца многочленов как алгебры и решение проблемы о корнях многочлена.
Для построения кольца многочленов как алгебры напомним определение алгебры.
Определение 1. Алгеброй называется упорядоченное множество двух множеств ![]() , где
, где ![]() множество элементов любой природы, а V – множество операций.
множество элементов любой природы, а V – множество операций.
Одной из алгебр является кольцо.
Определение 2. Кольцом называется алгебра с двумя бинарными операциями – сложение и умножение -, удовлетворяющих следующим свойствам:
< K, +> - аддитивная абелева группа; “ ´ ”- ассоциативная операция; Сложение и умножение связаны дистрибутивным законом.Для построения кольца многочленов зададим кольцо К и введем понятие многочлена.
Определение 3. Многочленом f(x) называется сумма anxn+an-1xn-1+...+a1x+a0, где aiÎ K, x – неизвестное, xÏ K, x0=1, 1·x= x. ai называют коэффициентами многочлена, an- старшим, a0 – свободным членом.
Определение 4. Суммой двух многочленов ![]() и
и ![]() называется многочлен h(x)=f(x)+g(x), h(x)=ckxk+...+c0, где ci=ai+bi. Определение 5. Произведением двух многочленов
называется многочлен h(x)=f(x)+g(x), h(x)=ckxk+...+c0, где ci=ai+bi. Определение 5. Произведением двух многочленов ![]() и
и ![]() называется многочлен
называется многочлен ![]() , где
, где ![]() .
.
Обозначим множество всех многочленов с коэффициентами из кольца K через K[x] и рассмотрим алгебру <K[x], +, ´ >. Докажем теорему о том, что эта алгебра является кольцом.
Теорема 6. Алгебра многочленов <K[x], +, ´ >, с коэффициентами из кольца K образует кольцо.
g 1. f(x)+(g(x)+h(x))=(f(x)+g(x))+h(x)
f(x)+g(x)=g(x)+f(x)
f(x)(g(x)h(x))=(f(x)g(x))h(x)
f(x)(g(x)+h(x))=f(x)g(x)+f(x)h(x)
Ассоциативность сложения и умножения, коммутативность сложения и дистрибутивные законы непосредственно вытекают из введенных нами операций над многочленами.
2. ![]() - называют нулевым многочленом, легко проверить, что
- называют нулевым многочленом, легко проверить, что ![]() , т.е.
, т.е. ![]() - выполняет роль нулевого элемента в алгебре K[x].
- выполняет роль нулевого элемента в алгебре K[x].
f(x)=(-an)xn+...+(-a1)x+(-a0)=-f(x) – называют противоположным многочленом для многочлена f(x), он выполняет роль противоположного элемента в алгебре. Так как все аксиомы кольца выполняются, то <K[x],+,´ > - кольцо, которое обозначают K[x] и называют кольцом многочленов над кольцом K.
Теорема 7. Если K область целостности, то K[x] тоже область целостности.
Для доказательства этой теоремы введем понятие степени многочлена.
Степенью многочлена f(x) называется максимальный показатель степени x с коэффициентом отличным от нуля. Обозначение: deg f(x)=n, где an¹ 0.
Степень многочлена обладает свойствами:
deg (f + g) £ max (deg f, deg g); deg (fg) = deg f + deg g, если K – область целостности. Доказательство свойств степени многочлена осуществляется на основе двух аргументов: во-первых, на основании выполнения операций; во-вторых, на основании целостности K.
Приступим к доказательству теоремы. Требуется проверить выполнимость: (1) коммутативности умножения и (2) отсутствие делителей нуля.
коммутативность умножения следует из определения умножения многочленов над областью целостности, где умножение элементов коммутативно.
f(x)¹ ![]() , deg f(x)=n³ 0, g(x)¹
, deg f(x)=n³ 0, g(x)¹ ![]() , deg g(x)=m³ 0,
, deg g(x)=m³ 0,
deg (f(x)g(x))=deg f(x)+deg g(x)= n+m ³ 0 Þ deg (fg) = n+m ³ 0 Þ $ cn+m ¹ 0 Þ (fg)¹ ![]() , это и доказывает отсутствие делителей нуля в K[x], где K – область целостности.
, это и доказывает отсутствие делителей нуля в K[x], где K – область целостности.
Пусть возникла ситуация, где требуется многочлен f(x) = anxn+...+a1x+a0 разделить на двучлен (x-a). Это можно сделать с помощью алгоритма, который принято в математике называть схемой Горнера. Построим этот алгоритм.
f(x) = (x-a)g(x)+r(x), где f(x) = anxn+...+a1x+a0, g(x)= bnxn+...+b1x+b0 .
Воспользуемся свойством степени, получим:
deg f(x) £ deg [(x-a)g(x)+r(x)]£ max[deg (x-a)g(x), deg r(x)]
deg (x-a)g(x)=deg (x-a)+deg g(x). Из этих равенств можно сделать вывод, что m=n-1, deg r(x)=0, т.е. r(x) – число, т.е. anxn+an-1xn-1+...+a1x+a0=(x- -a)bnxn+...+b1x+b0+r. Раскроем скобки справа и приравняем коэффициенты многочленов. Для удобства одновременно воспользуемся схемой.
| an | an-1 | ... | A2 | a1 | a0 | |
| a | bn-1 | bn-2=abn-1+an-1 | ... | b0=ab1+a1 | b0=ab1+a1 | r=ab0+a0 |
anxn=bn-1xn Þ bn-1=an
an-1xn-1=bn-1xn(-a)+bn-2xn-1 Þ an-1=bn-1(-a)+bn-2 Þ bn-2=an-1+abn-1
b1=ab2+a2, b0=ab1+a, r=ab0+a0.
Введем понятие корня многочлена.
Определение 8. Число x=a называется корнем многочлена f(x), если значение многочлена f(a) равно нулю.
Рассмотрим теорему Безу о делении многочлена на двучлен (x-a).
Теорема 9. (Безу) Остаток от деления многочлена f(x) на двучлен (x-a) равен f(a).
g f(x), (x-a). Поделим, f(x)=(x-a)g(x)+r, мы установили, что r – число. Подставим x=a в равенство, получим f(a)=0g(a)+r, откуда вытекает утверждение теоремы f(a) = r.
Из теоремы вытекает следствие: f(x)M (x-a) Û x=a корень уравнения.
Þ f(x) M (x-a) Þ f(x)=(x-a)g(x)+f(a) (по теореме Безу), f(a)=0 Þ x=a корень f(x)
Ü Пусть x=a корень многочлена, т.е. f(a)=0 Þ f(x)=(x-a)g(x) (по теореме Безу), т.е. f(x) M (x-a).
Вопрос 11. Кольцо многочленов над полем комплексных чисел.
В алгебре многочленов имеют место две взаимно пересекающиеся, взаимно дополняющие линии. Это вопросы существования и количества корней многочлена и разложение многочлена на неприводимые множители.
В вопросе представлено решение этих аспектов для кольца многочленов над полем комплексных чисел, т.е. для кольца C[x], где C – поле комплексных чисел.
Итак, пусть P – поле.
Определение 1. Поле P называется алгебраически замкнутым, если любой многочлен положительной степени имеет в этом поле корень. Алгебраической замкнутостью обладает поле C, это решается основной теоремой алгебры.
Теорема 2. Любой многочлен положительной степени из кольца C[x] обладает по крайней мере одним корнем. Примем эту теорему без доказательства в силу того, что она требует предварительного доказательства ряда теорем из математического анализа.
Из основной теоремы алгебры вытекает ряд следствий, их и рассмотрим.
Следствие 3. Неприводимым над полем C многочленом является многочлен только первой степени.
Для доказательства этого утверждения введем определения приводимого и неприводимого многочлена. Многочлен f(x)Î P[x] называется приводимым, если его можно представить в виде произведения двух многочленов меньшей положительной степени. В противном случае многочлен называется неприводимым.
Приступим к доказательству следствия 3.
Пусть дан f(x)Î C[x]. Пусть он приводим. Покажем, что
рассмотрим f(x)=a1x+a0, degf(x)=1. Предположим, что f(x) – приводим. Тогда по определению приводимого многочлена f(x)=f1(x)f2(x), где degf1(x)>0, degf2(x)>0. Однако по условию degf(x)=1=1+0=0+1, то есть degf1(x)=0È degf2(x)=0, что противоречит свойству степеней. Полученное противоречие и доказывает неприводимость многочлена (а1х+а0).Пусть deg f(x)>1, тогда по основной теореме алгебры он обладает корнем. Пусть таким корнем будет х=а. По следствию из теоремы Безу: f(x)=(x-a)f1(x). Так как deg(x-a)=1, degf(x)>1, deg(x-a)f1(x)=deg(x-a)+degf1(x), то degf(x)>0; то есть f(x) – приводим, что противоречит условию. Таким образом, неприводимым над полем С является только многочлен первой степени.
Следствие 4. Если f(x)Î C[x], degf(x)=n³ 1, то его можно представить в виде:
с(x-a1)(x-a2)...(x-an), (*)
где ai – корни его, а сÎ С.
g Пусть f(x)=c1x+c0=c1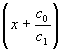 =c1(x-a1), где
=c1(x-a1), где ![]() ,то есть для многочлена f(x) утверждение верно: он представляется в виде (*) и а1– корень его, а с1– старший коэффициент.
,то есть для многочлена f(x) утверждение верно: он представляется в виде (*) и а1– корень его, а с1– старший коэффициент.
Далее, проведем доказательство методом математической индукции. Пусть теорема верна для многочлена степени меньшей или равной (n-1), то есть
f(x)=c(x-a1)...(x-an-1), где a1, a2, ..., an-1– его корни, а с – старший коэффициент.
Пусть f(x) – неприводим, а это возможно только для n=1, для этого случая теорема верна. Либо f(x) – приводим, тогда f(x)=g(x)h(x), где степени g(x) и h(x) меньше n, для них теорема верна. В силу свойства степени f(x)=c(x-a1)...(x-an), то есть множителей будет ровно n. По следствию из теоремы Безу аi – корни f(x), если расткрыть скобки в правой части и воспользоваться равенством многочленов, то с – старший коэффициент f(x). Теорема доказана.
Из этого в следствии с необходимостью вытекает еще два.
Следствие 5. Количество комплексных коней многочлена f(x)Î C[x] совпадает с его степенью.
Следствие 6. Любой многочлен f(x)Î C[x] положительной степени n можно представить в виде:
f(x)=c(x-a1)a 1(x-a2)a 2...(x-ak)a k, где a 1+...+a k=n, ai – его корни. Такое представление носит название канонического. Возможность такого представления вытекает из следствия (4) и допустимости повторяющихся корней, то есть кратных корней многочлена.
В теории многочленов над С имеет место теорема, устанавливающая связь между корнями многочлена и его коэффициентами.
Теорема 7. Пусть f(x)Î C[x], degf(x)=n, an=1 (то есть f(x) – нормирован), тогда как известно, f(x)=(x-a1)(x-a2)...(x-an), где имеет место соотношение:
а0 = (-1)n a1 a2 ... an;
a1= (-1)n-1 (a1a2 ... an-1+ ... + a2a3 ... an);
. . . . . . . . .
an-2= a1a2+ a1a3+ ... + an-1an ;
an-1= -(a1+ a2+ ... +an);
эти соотношения называются формулами Виета. Однако, справедливости ради, надо отметить, что Виет нашел эту зависимость только для случая положительных корней, в общем виде эта теорема установлена А. Жирарое.
Вопрос 12 Кольцо многочленов над полем действительных чисел (R).
В алгебре имеет место теория многочленов. Многочлен введен по определению как выражение f(x)=anxn+an-1xn-1+...+a1x+a0, где aiÎ K – кольцо, x0=1, 1·x= x. Введение операций “+” и “´ ” многочленов позволило построить алгебру многочленов, которой является кольцо многочленов над кольцом К и обозначается К[x]. Особый интерес представляет теория многочленов, когда вместо кольца К взято поле. Такими числовыми полями являются C, R, Q.
В силу существования операции деления в поле, стало возможным рассматривать два взаимосвязанных вопроса в теории многочленов: корни многочлена и разложение многочлена на неприводимые многочлены.
Рассмотрим решение этой проблемы для кольца многочленов над R.
Теорема 1. Комплексные корни f(x)Î К[x], то есть с действительными коэффициентами попарно сопряженными.
n Пусть f(x)Î К[x], и пусть z=a+bi; a,bÎ R комплексное число, являющееся корнем f(x), причем degf(x)³ 2 в противном случае f(x) комплексных корней иметь не может. Покажем, что ![]() =a–bi, b¹ 0 тоже является корнем f(x).
=a–bi, b¹ 0 тоже является корнем f(x).
f(![]() )=an
)=an![]() n+an-1
n+an-1![]() n-1+...+a1
n-1+...+a1![]() +a0= (воспользуемся свойством сопряжения) = =
+a0= (воспользуемся свойством сопряжения) = =![]() , то есть
, то есть ![]() является корнем f(x), что и требовалось доказать.
является корнем f(x), что и требовалось доказать.
Рассмотренная выше теорема позволяет доказать теорему о неприводимом многочлене из R[x]. Напомним определение приводимого и неприводимого многочленов.
f(x) называется неприводимым, если его можно представить в виде произведения двух многочленов меньшей положительной степени и неприводимым, если этого сделать нельзя.
Рассмотрим f(x)= a1x+a0, aiÎ R. его нельзя представить в виде произведения двух многочленов меньшей положительной степени в силу того, что 1=1+0=0+1.
Решать будем вопрос о приводимости и неприводимости многочлена f(x)Î R[x] степени большей или равной 2.
Теорема 2. Неприводимый многочлен f(x)Î R[x], degf(x)=n³ 2 ассоциирован с многочленами (x-a)2+b2,где x=a+bi комплексный его корень.
n Пусть f(x)Î R[x], degf(x)=n³ 2, пусть x=a+bi, b¹ 0 – корень f(x), он неприводим.
Прежде всего отметим, что у такого многочлена нет действительных корней, иначе бы f(x)=(x-a) f1(x) (следствие из теоремы Безу), что противоречило бы его неприводимости.
По теореме о сопряженности мнимых корней многочлена с действительными коэффициентами f(x) обладает еще одним корнем x2=a–bi, где x2=![]() .
.
Рассмотрим (x-x1)(x-x2)=(x-a)2+b2. (*)
Разделим f(x) на многочлен (*), получим:
f(x)=[(x-a)2+b2]g(x)+r(x).
Так как степень делителя равна 2, то degr(x)<2, то есть r(x)=cx+d. Подставим в (1) x1=a=bi и x2=a-bi, мы получим: ![]()
Так как b¹ 0 , то c=0, тогда d=0, то есть r(x)=![]() .
.
Это означает, что f(x)M (*). Но f(x) – неприводим, потом deg g(x)=0, то есть g(x)Î R. Что и подтверждает ассоциированность f(x) и (*).
Теорема 3. Рассмотренная выше теорема позволит сделать ряд выводов:
Неприводимыми многочленами над R могут быть многочлены не выше второй степени. Многочлен f(x)Î R[x], degf(x)³ 1 может быть представлен в виде:![]() , где
, где ![]() если среди корней есть кратные, то можно представить и в виде (*):
если среди корней есть кратные, то можно представить и в виде (*):
![]() , где Si – кратности корней, а tj – кратности сопряженных мнимых его корней. Представление (*) называется каноническим представлением f(x).
, где Si – кратности корней, а tj – кратности сопряженных мнимых его корней. Представление (*) называется каноническим представлением f(x).
Теорема 4. Теоремы (1), (3) позволяют сделать с очевидностью вывод о том, что четность действительных корней совпадает с четностью его степени.
Вопрос 13. Кольцо многочленов над полем рациональных чисел (Q).
Теория многочленов утверждает, что множество многочленов f(x) = an xn + …+ a1 x + a0,
где ai ∈K – кольцо, x0=1, x∈K, 1∙x=x с операциями сложения и умножения образуют кольцо многочленов над кольцом K и обозначают K[x].
Особый интерес представляет теория многочленов, когда вместо кольца K рассматривается поле P. В силу того, что в поле P есть операция деления, становится возможным построить теорию корня многочленов и теорию приводимых и неприводимых многочленов. Рассмотрим, как решается эта проблема в Q[x].
Напомним, что корнем f(x) называется такое число x=a, что f(a)=0.
f(x) называется неприводимым, если его нельзя представить в виде двух многочленов меньшей положительной степени, в противном случае его называют приводимым.
Итак, пусть Q[x], f(x)∈ Q[x], где f(x) = an xn + …+ a1 x + a0 …(1), сформулируем и докажем теорему о рациональных корнях многочлена с целыми коэффициентами. Если многочлен имеет рациональные коэффициенты, то он легко преобразуется к ему ассоциированному с целыми коэффициентами. Поэтому теорию существования и нахождения корней f(x)∈ Q[x] рассматривают именно для такого варианта, т.е. f(x)∈ Q[x], а ai ∈Z.
Теорема 1: Если ![]() ∈Q, где (p,q)=1, является корнем многочлена (1)… f(x) = an xn + …+ + a1 x + a0, ai ∈Z, то p является делителем свободного члена, а q-делителем старшего коэффициента an.
∈Q, где (p,q)=1, является корнем многочлена (1)… f(x) = an xn + …+ + a1 x + a0, ai ∈Z, то p является делителем свободного члена, а q-делителем старшего коэффициента an.
■ Если ![]() ∈Q корень f(x), то f
∈Q корень f(x), то f ![]() =0. Подставим в (1)
=0. Подставим в (1) ![]() вместо x, получим
вместо x, получим
0= an ![]() + …+ a1
+ …+ a1 ![]() + a0, приведём к общему знаменателю, получим
+ a0, приведём к общему знаменателю, получим
0= an pn + an-1 pn-1 q+…+ a1 p qn-1 + a0 qn …(2).
Преобразуем (2):
2.1: 0 = an pn + q(an-1 pn-1 +…+ a1 p qn-2 + a0 qn-1) ⇒ an pn + q Q∶q, qQ∶q
⇒ an pn ∶q, (p,q)′→ an∶q, т.е. q-делитель старшего коэффициента;
2.2: 0 = p(an pn-1 +…+ a1 qn-1 ) + a0 qn) ⇒ pQ + a0 qn∶ p, pQ∶ p, ⇒ a0 qn∶ p, (q,p)=1 ⇒ a0 ∶ p, т.е. p-делитель свободного члена, что и доказывает теорему.
Следствие 2: Если f(x)∈ Q[x], а ai ∈Z, an=1, то он обладает только целыми корнями, которые находятся среди делителей свободного члена.
Истинность этого утверждения очевидна в силу того, что an=1, а делители 1 являются только ±1, следовательно, q=±1 и ![]() ∈Z. Т.к.
∈Z. Т.к. ![]() = ± p∈Z находятся среди делителей, то утверждение верно.
= ± p∈Z находятся среди делителей, то утверждение верно.
Решим проблему неприводимости многочлена из Q[x], вернее о степени такого многочлена.
Решение этой проблемы предложено Эйзенштейном и носит название критерий Эйзенштейна о неприводимости многочлена в Q[x]. Заметим, что решение этой проблемы тоже есть смысл рассматривать для f(x)∈ Z[x], поскольку Q является полем частных области целостности Z.
Теорема 3: Пусть f(x)= cn xn + …+ c1 x + c0, ci ∈Z. Пусть все коэффициенты f(x), кроме старшего, делятся на p2. Тогда f(x) неприводим в Z[x].
■ Доказательство проведём методом от противного.
Пусть f(x)∈ Q[x] или f(x)∈ Z[x] приводим, т.е. существуют такие g(x), h(x)∈ Z[x], что
f(x) = (a0 +…+ak xk )(b0 +…+ bm xm) = g(x)·h(x), (ak ≠ 0, bm ≠ 0, k + m = n, причем 1≤ k, m<n).
Тогда c0 = a0·b0, cn = ak·bm. Так как c0∶p, c0 не∶p2, c0 = a0·b0 ⇒ a0 не∶p Λ b0 не∶p; пусть a0∶p,
b0 не∶p. Так как cn не∶p, то ak не∶p, bm не∶p, тогда у g(x) есть коэффициент делящийся на p и неделящийся на p. Пусть as коэффициент g(x) с наименьшим s таким, что as не∶p, т.е. a0, a1, …, as-1∶p, а as не∶p.
Найдем cs = as bs + (as-1 b1 + a0 bs) (s<n), т.к. as не∶p, b0 не∶p, то as b0 не∶p, число (as-1 b1 + a0bs) ∶p, по свойству делимости в кольце Z, cs не∶p, s<n, а это противоречит условию. Получено противоречие в силу предположения, что f(x) - приводим. Что и доказывает теорему о неприводимости f(x).
Следствие 4: Если p – простое число и n – любое целое положительное число, то многочлен xn-p неприводим в Q[x].
Теорема 3 и следствие 4 позволяют сделать вывод о том, что в Q[x] существуют неприводимые многочлены любой степени. Поэтому решение проблемы нахождения корней f(x) и разложения его на неприводимые многочлены затрудненно и требует в каждом конкретном случае особого подхода.
Вопрос 14. Простое алгебраическое расширение поля.
Пусть дано поле P. P[x]- кольцо многочленов от одной переменной над полем P. Обратимся к понятию алгебраической замкнутости поля P. Напомним, что поле Р называется алгебраически замкнутым, если любой многочлен f(x)Î P[x] обладает хлтя бы одним корнем. Введем такое понятие: элемент a Î Р называется алгебраическим над полем Р, если существует f(x)Î P[x], для которого a является корнем.
Пусть дано поле Р и a Ï Р, a Î F – поле.
Определение 1. Простым расширением поля Р с помощью элемента a называется наименьшее подмножество поля F, содержащее Р и a . Простое расширение поля Р с помощью a Î F обозначается Р(a ).
В вопросе решается проблема о строении Р(a ) и возможности применения этой теории для освобождения знаменателя дроби от алгебраической иррациональности. Для решения обозначенной проблемы рассмотрим Р[a ]={f(a )/f(x)Î P[x]}, где Р[a ]={a0+a1a +...+ana n/aiÎ P, nÎ N}.
Легко проверить, что Р[a ] подкольцо поля Р(a ).
Теорема 2. Пусть Р[x] – кольцо над Р, Р(a ) – простое расширение Р с помощью элемента a . Пусть y : Р[х] на Р[a ] – отображение такое, что y (f(x))=f(a ). Тогда:
10. " aÎ P, y (a)=a ;
20. y (x)=a ;
30. y – гомоморфизм и эпиморфизм;
40. Ker y ={f(x)Î Р[x]/ f(a )=0Î Р[a ]};
50. Фактор-кольцо Р[х]/Ker y изоморфно кольцу Р[a ].
n 10 и 20 следуют из определения y .
30: y (f(x)+g(x))= f(a )+g(a ), y (fg)=f(a )g(a ), y (1)=1, это проверяется непосредственно, поэтому y – гомоморфизм; " f(a )Î Р[a ], $ f(x)Î Р[x], y (f(x))=f(a ) Þ y – эпиморфизм.
40: следует из существования Ker f для гомоморфизма и из определения y .
Рассмотрим 50. Так как Ker y – идеал Р[х], то становится возможным Р[х] факторизовать, получить Р[х]/Ker y , тогда по основной теореме об эпиморфизме колец Р[х]/Ker y º Р[a ].
e : Р[x]® Р[x]/Kery , e (f(x))=Kf(x).
j : Р[x]/Kery ® Р[a ], где
j (Kf(x))=f(a )Þ j – изоморфизм.
Следствие 3. Если a - трансцендентный элемент над полем Р, то Р[х]@ Р[a ].
n В силу трансцендентности a над Р, Kery ={0} и Р[x]/{0}@ Р[a ], кроме того e – изоморфизм, то есть Р[x]/{0}@ Р[x] следовательно, Р[x]@ Р[a ].
Определение 4. Пусть Р[х] – кольцо многочленов над полем Р. Пусть a – алгебраический элемент над полем Р. Минимальным многочленом * a над Р называется нормированный многочлен наименьшей степени, для которого a является корнем.
Обозначим минимальный многочлен для a над Р через g(x), deg g(x)=n называют степенью алгебраического элемента a над Р.
Легко показать:
g(x) существует для каждого алгебраического элемента; g(х) – неприводимый многочлен в Р[х] над Р; g(x) для a определяется однозначно. – вытекает из определения алгебраического элемента. – из определения минимальности g(x). – из предположения, что существует два многочлена * g и h и их неприводимости, они ассоциированы, а так как они неприводимы, то g(x)=h(x).Теорема 5. Пусть a алгебраический элемент степени n над Р (a Ï Р) и g(x) – его минимальный многочлен степени n, тогда имеют место:
10. Если f(a )=0, где f(x)Î Р[х], то f(x)M g(x);
20. Р[х]/(g(f))@ Р[х];
30. Р[х]/(g(f)) – поле;
40. Р[a ]=Р(a ).
n Пусть a корень f(x), то есть f(a )=0, известно, что g(a )=0, тогда (f,g) либо 1, либо нет. Первое невозможно, так как по известной теореме f(x)M (x-a ) и
g(x)M (x-a ). Следовательно, (f,g)¹ 1, то есть они не являются взаимно простыми, поэтому f(x) делится на g(x).
Зададим гомоморфизм y : Р[х]® Р[a ], y (f(x))=f(a )Þ Ker y ={f(x),f(a )=0} состоит из многочленов, делящихся на g(x), поэтому Ker y =J=(g(x)) – идеал Р[х]Þ Р[х]/(g(x)) @ Р[a ] (*), так как Р[a ]Ì Р(a ), то Р[a ] – область целостностиÞ Р[х]/(g(x)) в силу (*) тоже область целостности. Покажем, что любой элемент из Р[х]/(g(x)) ненулевой обратимый.
Пусть ![]() смежный класс,
смежный класс, ![]() , то f(a )=0, тогда f(x) не делится на g(x)Þ (f(x),g(x))=1Þ
, то f(a )=0, тогда f(x) не делится на g(x)Þ (f(x),g(x))=1Þ ![]() , но
, но ![]() Þ
Þ ![]() Þ
Þ ![]() , что и требовалось доказать, то есть Р[х]/(g(x)) – поле, а так как эта алгебра изоморфна Р[a ], то Р[a ] тоже поле являющееся подполем поля Р(a ). Но Р(a ) минимальное подполе поля F, следовательно, Р(a ) Ì Р[a ], откуда получаем, что Р[a ]=Р(a ).
, что и требовалось доказать, то есть Р[х]/(g(x)) – поле, а так как эта алгебра изоморфна Р[a ], то Р[a ] тоже поле являющееся подполем поля Р(a ). Но Р(a ) минимальное подполе поля F, следовательно, Р(a ) Ì Р[a ], откуда получаем, что Р[a ]=Р(a ).
Эта теорема позволяет установить строение простого алгебраического расширения Р(a ).
Пусть a - алгебраический элемент над P, а Р(a ) – простое алгебраическое расширение P, пусть степень a равна n>0. Тогда
Теорема 6. Любой элемент поля Р(a ) однозначно представим в виде линейной комбинации n элементов 1,a ,...,a n-1 с коэффициентами из P.
Вопрос 15. Простые и составные числа.
Рассмотрим N – натуральные числа. Введем понятие простого и составного числа.
Опр.1 N ' а называется делящимся на число вÎ N , в > 0, если существует такое число с, что а = вс, при этом а – делимое, в – делитель, с – частное.
Все натуральные числа, в связи с отношениеми делимости на , разбиваются на группы: { 0} , { 1} , { р1, р2,…,…} , { а1, а2,…} , где 1 обладает только один делитель, рi – двумя, а для аi существует более двух.
Опр.2 Натуральное число р называется простым, если оно имеет ровно два различных делителей. (1 и само число р), составным, если имеет более двух делителей.
Введенное определение позволит выражать числа натуральные через простые. Это описывается теоремой, которую называют основной теоремой арифметики.
Теорема. 3 Любое n Î N , n > 1 можно единственным образом представить в виде произведения простых чисел с точностью до перестановки сомножителя.
В теореме содержится две теоремы: о существовании разложения и его единственности.
(7) Пусть n Î N , n > 1. Для доказательства исследуем метод математической индукции.
n = 2, 2 – простое число, следовательно n = 2 и есть его разложение.
Предположим, что для любого натурального числа, меньшего n, теорема верна и докажем для n.
Пусть дано натурально n, если оно простое, то это и есть его разложение. Если n составное, тогда n = вс, где в,с Î N и меньше n. По предположению индукции разложение их на простые множители существует, поэтому оно существует и для n. На основании принципа математической индукции, можно утверждать истенность теоремы для любого n Î N , n > 1.
(!) Докажем единственность разложения на простые множетели методом математической индукции.
n = 2, 2 = 2. Разложение единственное.
Допустим, что для любого числа натурального, меньшего n утверждение справедливо и докажем для n. Если n простое число, то это и есть его разложение и оно единственно. Если n составное, то оно допустит разложение на простые числа. Предположим, что таких разложений оказалось два: n = p1p2 ¼ pк = q1q2 … qs (1). Из равенства (1) видно, что “правая часть” делится на p1. А т.к. в “правой части числа простые”, то
существует число qi, которое делится на p1; (p1, qi) = 1. Следовательно, p1 = qi. Пусть qi = q1, разделим обе части равенства (1) на p1, получим, что и “левая часть” и “правая часть” числа натуральные, меньше n, а для них разложение единственное с точночтью до перестановки сомножителя. Поэтому при соответственно мы получаем, что n = p1p2 ¼ pк – разложение n и это разбиение единственное. Что и требовалось доказать.Если среди простых множителей окажутся равные, то их объединяют в степень и получают представление n Î N в виде: ![]() , которое называют каноническим разложением натурального числа.
, которое называют каноническим разложением натурального числа.
В теории натуральных чисел имеет место теорема, решающая вопрос о количестве простых чисел во множестве N .
Теорема 4. (Евклида) Множество простых чисел в N бесконечно.
Проведем доказательство методо от противного.
Пусть простых чисел конечное число: p1p2 ¼ pк. Рассмотрим N = p1p2 ¼ pк+1. Исследуем полученное число:
1) N > 1 = > оно простое или составное; N ¹ pi, i = 1, к ;
2) N ![]() pi, , i = 1, к = > , т.к. при делении на pi получен остаток 1;
pi, , i = 1, к = > , т.к. при делении на pi получен остаток 1;
N – составное. Если N составное, то ему надлежит делиться на 1, N и еще на какое-нибуть простое число (см. ниже), но это не так, поэтому N не является составным. Полученное противоречие и доказывает теорему.
Теорема 5. Наименьший, отличный от 1 делитель составного числа, является простым числом.
Пусть n Î N имеет делители, отличные от 1. Обозначим тот делитель, который будет наименьшим среди всех делителей. Пусть это натуральное число к, т.е. n = к . m; к, m Î N , к > 1. Исследуем к.
Если к = p – простое число, то теорема верна.
Если к – составное число, то к = к1 m1, тогда n = к1 (m1 m), n ![]() к1, к1 < к, что противоречит выбранному наименьшему значению. Это и доказывает теорему.
к1, к1 < к, что противоречит выбранному наименьшему значению. Это и доказывает теорему.
Достаточно часто в математике приходитс для числа а Î N выяснять, является оно простым или составным. Для решения подобных задач предложен способ, носящий название “решето Эратосфена…” или способа отсеивания чисел кратных 2,3,…,p,… .
Опишем этот способ.
Если даны числа натурального ряда: 1,2,3,4,5,…,n, то для установления какими они являются: простыми или составными, поступают так: вычеркивают 1,2 и каждое второе, ибо каждое второе начинается от 3, делится на 2, поэтому является составным. Затем повторяем эту процедуру для 3. 3 вычеркивается и каждое третье, ибо 6 – третье по счету за 3, делится на 3. названную процедуру повторяют до простого числа с не превосходящего ![]() . Оставшиеся числа являются простыми.
. Оставшиеся числа являются простыми.
Такой алгоритм можно использовать и для установления чисел в промежутке от n1 до n2.
Опишем его спецификацию . Если надо установить какие числа в промежутке от n1 до n2 являются простыми, то поступим так:
выясним простое или составное является число n1:
Проверим его делимость на 2,3,5,…p ≤ ![]() . Если оно не делится на эти простые числа, то оно простое;
. Если оно не делится на эти простые числа, то оно простое;
Если оно делится хотя бы на одно из этих чисел, то оно составное.
при выяснении простого числа n, одновременно поступаем так:
2.1 если n1![]() 2, то вычеркивают его и каждый второй (как в первом случае); и переходим к (n1 + 1);
2, то вычеркивают его и каждый второй (как в первом случае); и переходим к (n1 + 1);
2.2 если n1 ![]() 2, то к числу добавляем 1 и вычеркиваем n1 + 1 и любое второе за ним;
2, то к числу добавляем 1 и вычеркиваем n1 + 1 и любое второе за ним;
2.3 если было 2.1, то переходим к (n1 + 1) и проверяется делим его на 3, повторяем процедуру решета Эратосфена переходит к (n1 + 2);
2.4 Если было 2.2, то проверяют делимость на 3;
2.4.1. если n1![]() 3, то проверяю решето Эратосфена и переходят следующему.
3, то проверяю решето Эратосфена и переходят следующему.
не вычеркнутому числу и исследуют его делимое на 5;
2.4.2. если n1 = 3q + r, то в зависимости от r = 1 или r = 2, добавляем 1 или 2 и
n1 + 1, n1 + 2.
И любое третье по счету и т.д.
2.5 Если n1 оказалось простым, то все не вычеркнутые числа тоже простые. Если n1 оказалось составным, а ni – простое, то все стоящие за ni числа остальные простые.
Похожие работы
... кадров профессионалов. Существует мнение, что профессиональный уровень управленческого персонала обеспечивается знанием производства и опытом управленческой работы, по необходимости дополненными краткосрочными курсами повышения квалификации или переподготовки. Это ошибочное мнение. Профессиональное мышление формируется на ранних стадиях получения высшего образования и профессиональной ...
... и это также под контролем, так как внеклассные интересы якобы отвлекали детей от занятий, и учащихся окружали всевозможные запреты. Таким образом, культурно-бытовой облик учащихся начальной и средней школы в XIX – начале XX века отличали две его специфические черты: возраст учащихся (они постоянно находились в стадии развития) и попытки непрерывного контроля над этим развитием самого учебного ...
... -педагогическая или научно-техническая проблема, являющаяся новым научным вкладом в теорию определенной области знаний (педагогику, технику и другие). 4. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ВЫПОЛНЕНИЯ ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЫ БАКАЛАВРА ФИЗИКО-МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ ПРОФИЛЬ ИНФОРМАТИКА 4.1. Положение о выпускной квалификационной работе бакалавра физико-математического образования: ...
... ; технологическая функция имеет подфункции экономии учебного времени и учебного материала, устранения его дублирования и т.д. ГЛАВА 4. СОДЕРЖАНИЕ ИСНТРУМЕНТАЛЬНО-МЕТОДОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ ПЕДАГОГИЧЕСКОЙ ИНТЕГРАЦИИ 4.1. Типология интегративно-педагогического исследования В связи с поднимаемой в данном параграфе проблемой большой интерес вызывает монография В.М.Полонского "Оценки ...
0 комментариев