Навигация
3.1.1.2. Примеры.
1) Дана некоторая диаграмма касательных усилий (на пальце кривошипа) для некоторой паровой машины. В связи с вопросом о крутильных колебаниях вала представляет интерес выделить гармонические составляющие касательного усилия Т как функции от угла 
поворота кривошипа. Сняв с графика двенадцать равноотстоящих ординат, произведем гармонический анализ по указанной схеме:
| T | -7200 | -300 | 7000 | 4300 | 0 | -5200 | -7400 |
| 250 | 4500 | 7600 | 3850 | -2250 | |||
| U | -7200 | -50 | 11500 | 11900 | 3850 | -7450 | -7400 |
| V | -550 | 2500 | -3300 | -3850 | -2950 |
| u | -7200 | -50 | 11500 | 11900 |
| -7400 | -7450 | 3850 | ||
| s | -14600 | -7500 | 15350 | 11900 |
| d | 200 | 7400 | 7650 |
| V | -550 | 2500 | -3300 |
| -2950 | -3850 | ||
|
| -3500 | -1350 | -3300 |
|
| 2400 | 6350 |
Теперь по формулам (12):
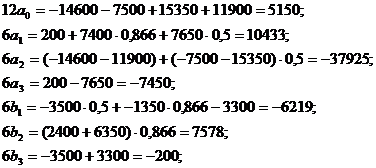
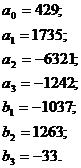
Таким образом,
Объединим члены, содержащие косинус и синус одного и того же угла:
Мы видим, что наиболее сильное влияние здесь оказывает вторая гармоника.
2) Для того чтобы дать себе отчет в том, с какой примерно точностью получаются коэффициенты Фурье функции по двенадцати ординатам ее графика, мы приложим изложенный метод к некоторым аналитически заданным функциям и сравним приближенные результаты с точными.
Сначала рассмотрим функцию 
, которую в промежутке 
задается формулой
,
А для остальных значений x определяется по закону периодичности
.
Вычислим табличку:
| x | 0 |
|
|
|
|
|
|
|
|
|
|
| 2 |
| y | 0 | 0.400 | 0.582 | 0.589 | 0.465 | 0.255 | 0 | -0.255 | -0.465 | -0.589 | -0.582 | -0.400 | 0 |
При этом можно использовать легко проверяемое тождество:
По схеме Рунге по этим значениям yнайдем:
b1=0.608; b2=0.076; b3=0.022;
все числа 
, а с ними и все коэффициенты 
оказываются нулями.
В то же время формулы (10) непосредственно дают (с помощью трехкратного интегрирования по частям):
,
Так что
; 
; 
.
Совпадение превосходное!
3) Однако далеко не всегда получается столь точный результат. В виде второго примера мы возьмем функцию с периодом 
, которая в промежутке определяется так:
.
Пользуясь тождеством:
,
составим таблицу:
| x | 0 |
|
|
|
|
|
|
|
|
|
|
| 2 |
| y | 1 | 0,694 | 0,444 | 0,250 | 0,111 | 0,028 | 0 | 0,028 | 0,111 | 0,250 | 0,444 | 0,694 | 1 |
Тогда по схеме Рунге
числа же 
и коэффициенты 
- на этот раз нули. Точные значения коэффициентов будут:
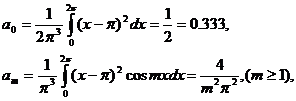
в частности,
; 
; 
.
Таким образом, если для первых двух коэффициентов относительная погрешность не превосходит 1,5-2 %, то для последующих она достигнет10% и даже 20%! Ясно, что для повышения этой точности нужно брать больше ординат.
Похожие работы
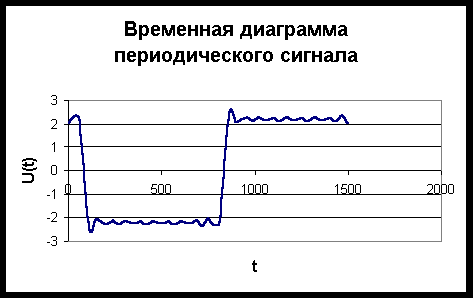
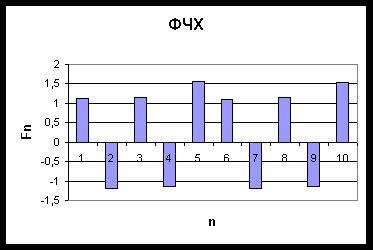
... . Сигнал задан в виде функции времени U(t) , повторяющийся с периодом Т. Требуется выполнить спектральный анализ сигнала и построить графики амплитудного и фазового спектров сигнала. 2.Численные методы расчетов спектральных и временных характеристик периодических сигналов Для расчета спектральных и временных характеристик периодического сигнала используем численные методы, чтобы упростить ...
... , либо функция задана таблично , нахождение интеграла по формуле Ньютона-Лейбница невозможно. Используют приближенные формулы, которые называют квадратурными, либо формулами численного интегрирования. 1) Формулы прямоугольника Пусть y=f(x) непрерывна на [a,b]. Требуется вычислить . Разобьем отрезок интегрирования на n равных частей, точками xi, i=0,n xi=a-i*h шаг ...
... для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5 Ответ: B= Решить задачу 5, используя соотношения (8) и (9). Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел. Переменный ток долгое время не находил практического ...
... системам линейных алгебраических уравнений с более чем одной неизвестной; MATLAB решает такие уравнения без вычисле-ния обратной матрицы. Хотя это и не является стандартным математическим обозначением, система MATLAB использует терминологию, связанную с обычным делением в одномерном случае, для описания общего случая решения совместной системы нескольких линейных уравнений. Два символа деления / ...
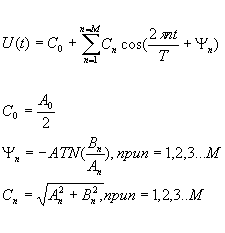
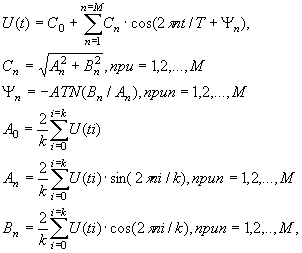
0 комментариев