Навигация
Быстрое преобразование Фурье
22876
знаков
13
таблиц
6
изображений
3.1.2.3. Быстрое преобразование Фурье.
Осуществление прямого и обратного дискретных преобразований Фурье
Является составной частью решения многих задач решения многих задач. Непосредственное осуществление этих преобразований по формулам (4), (7) требует 
арифметических операций. Рассмотрим вопрос о возможности сокращение этого числа. Для определенности речь пойдет о вычислении коэффициентов 
по заданным значениям функции. Идея построения алгоритмов быстрого преобразования Фурье опирается то, что при составном N в слагаемых правой части (7) можно выделить группы, которые входят в выражения различных коэффициентов . Вычисляя каждую группу только один раз, можно значительно сократить число операций.
Рассмотрим сначала случай 
. Представим q, j, лежащие в пределах 
, в виде 
, где 
. Имеем цепочку соотношений
.
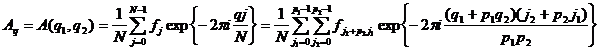Из равенства
и предыдущего соотношения получим
,
где
.
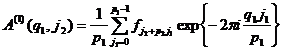Непосредственное вычисление всех 
требует 
арифметических операций, а последующее вычисление 
- еще операций. Поэтому при 
общее число операций составит 
. Точно так же при 
строится алгоритм вычисления совокупности значений , для которого общее число операций не превосходит 
, здесь С – постоянная, не зависящая от N. Выпишем соответствующие расчетные формулы для наиболее употребительного случая 
. Представим числа q, l в виде
,
где 
. Величину 
представим в виде
,
где s - целое, равное сумме всех слагаемых вида 
, которых 
. Очевидно, что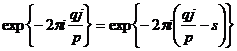 
, поэтому
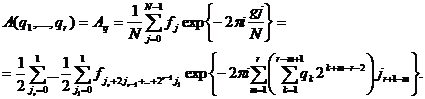
После перегруппировки слагаемых имеем
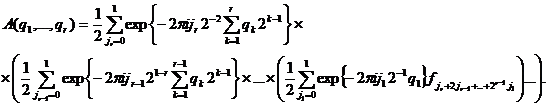
Это соотношение можно записать в виде последовательности рекуррентных соотношений
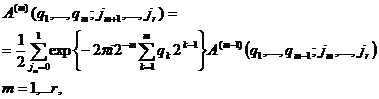
где
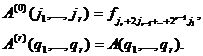
Переход от каждой совокупности 
к совокупности 
требует O(N) арифметических и логических операций; всего таких шагов r, поэтому общее число операций имеет порядок 
.
Вычисление при помощи совокупностей дает меньшее накопление вычислительной погрешности по сравнению с формулами (3.7). Определенные удобства имеются также при вычислении экспонент, входящих в расчетные формулы. При вычислении величин используются значения 
, 
. В частности, при m=1 величина 
принимает значения +1 или -1. Для вычисления значений 
потребуются еще значения 
при нечетных j, удовлетворяющих неравенству 
. Их можно вычислить через уже вычисленные до этого величины, в частности, при помощи соотношений 
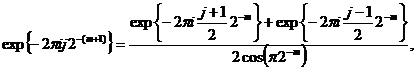
где, в свою очередь,
при 
.
В ряде случаев удается еще уменьшить число операций. Один из таких случаев упоминался выше: дана вещественная функция 
, известная в точках 
; требуется найти коэффициенты интерполяционного многочлена
.
Другой случай: при четном N заданы значения функции
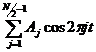
в точках 
; нужно определить коэффициенты 
.
3.1.3. Расчет коэффициентов на ЭВМ.
Было запрограммировано два метода расчета коэффициентов на языке Паскаль:
по схеме Рунге;
метод трапеций.
3.1.3.1. Схема Рунге.
Расчет ведется для двенадцати орт. Для большего количества ординат алгоритм остается аналогичным с небольшими корректировками в основной части программы (необходимо заменить вычислительные формулы для коэффициентов). См. приложение 1.
Похожие работы
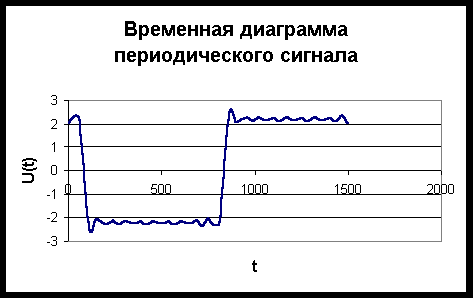
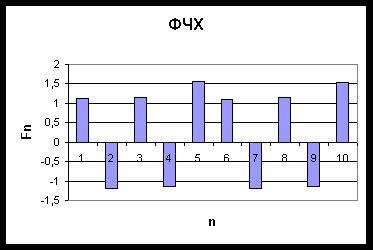
... . Сигнал задан в виде функции времени U(t) , повторяющийся с периодом Т. Требуется выполнить спектральный анализ сигнала и построить графики амплитудного и фазового спектров сигнала. 2.Численные методы расчетов спектральных и временных характеристик периодических сигналов Для расчета спектральных и временных характеристик периодического сигнала используем численные методы, чтобы упростить ...
... , либо функция задана таблично , нахождение интеграла по формуле Ньютона-Лейбница невозможно. Используют приближенные формулы, которые называют квадратурными, либо формулами численного интегрирования. 1) Формулы прямоугольника Пусть y=f(x) непрерывна на [a,b]. Требуется вычислить . Разобьем отрезок интегрирования на n равных частей, точками xi, i=0,n xi=a-i*h шаг ...
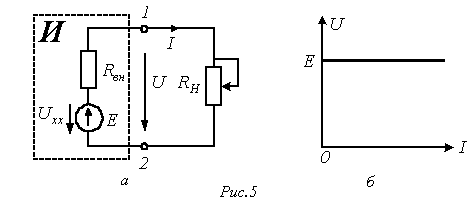
... для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5 Ответ: B= Решить задачу 5, используя соотношения (8) и (9). Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел. Переменный ток долгое время не находил практического ...
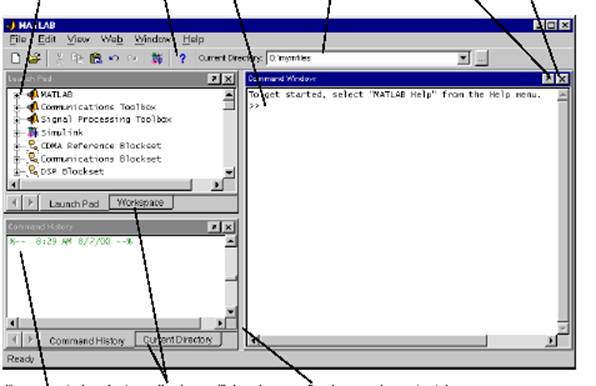
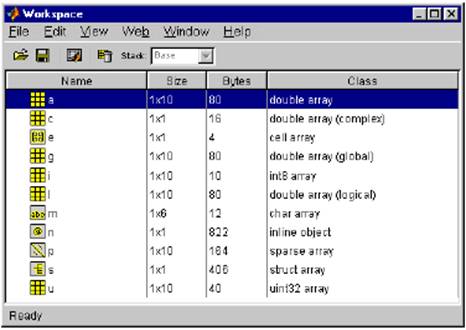
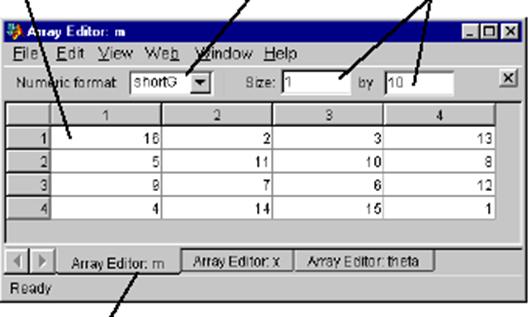
... системам линейных алгебраических уравнений с более чем одной неизвестной; MATLAB решает такие уравнения без вычисле-ния обратной матрицы. Хотя это и не является стандартным математическим обозначением, система MATLAB использует терминологию, связанную с обычным делением в одномерном случае, для описания общего случая решения совместной системы нескольких линейных уравнений. Два символа деления / ...
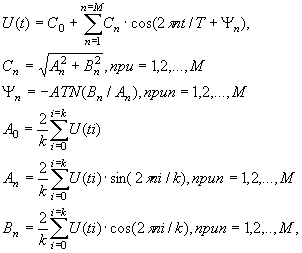
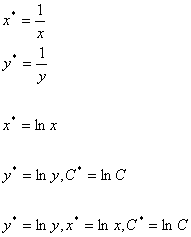
0 комментариев