Навигация
Быстрое преобразование Фурье
22876
знаков
13
таблиц
6
изображений
3.1.2. Быстрое преобразование Фурье.
Тригонометрическая интерполяция. Дискретное преобразование.
Дискретное преобразование Фурье применяется при решении многих прикладных задач. К ним относится тригонометрическая интерполяция, вычисление сверстки функций, распознавание образов и многие другие. Дискретное преобразование Фурье стало особенно эффективным методом решения прикладных задач после создания быстрого преобразования Фурье.
Пусть f(x) – периодическая функция с периодом 1 – разложена в ряд Фурье
, (1)
причем
. (2)
Здесь i – мнимая единица.
Рассмотрим значение этой функции на сетке из точек 
, где l, N целые, N фиксировано, и обозначим 
. Если 
, где k целое, то 
, где kl целое. Следовательно,
(3)
в узлах сетки. Поэтому если функция f(x) рассматривается в узлах сетки 
, то в соотношении (1) можно привести подобные члены
, (4)
где
. (5)
Лемма. При 
, определяемых (5), соотношение (4) остается в силе, если пределы суммирования [0, N-1] заменить на [m,N-1+m], где m – любое целое.
Если с самого начала была задана функция, определенная только на сетке, то на этой сетке ее можно также представить в форме (1). Действительно, такую функцию можно продолжить на всю прямую, доопределив ее между узлами сетки путем линейной интерполяции. Для непрерывной кусочно-дифференцируемой функции выполняется (2), поэтому в точках сетки после приведения подобных членов получим (4).
Определим скалярное произведение для функции на сетке следующим образом:
.
(Множитель 
введен для согласованности получаемых соотношений с непрерывным случаем: если f(x) и g(x) – непрерывные функции на отрезке [0,1], то вследствие интегрируемости f(x)g(x) по Риману
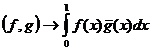
при 
). Функции 
при 
образуют ортогональную систему относительно введенного таким образом скалярного произведения. Действительно,
.
При 
, суммируя геометрическую прогрессию, имеем
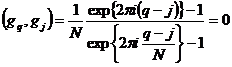
(при 
знаменатель отличен от 0). Поскольку 
, то в итоге имеем
при 
. (6)
Умножая (4) скалярно на 
, получим равенство
(7)
Выражение в правой части образует квадратурную сумму для интеграла
,
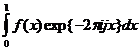поэтому
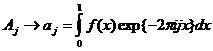
при и фиксированном j.
Покажем, что соотношение
(8)
в общем случае не имеет места. Пусть 
. Из (4) получаем 
, остальные 
. Таким образом, правая часть (8) есть 
. Она совпадает с f(x) в точках , но, как правило, далека от нее вне этих точек.
Воспользовавшись утверждением леммы, перепишем (4) в виде
. (9)
Если f(x) – достаточно гладкая функция, то величины 
с ростом j убывают быстро, поэтому 
при малых q. Кроме того, при гладкой f(x) величины и 
малы при больших q.
Напомним, что это приближенное равенство обращается в точное равенство в точках сетки. Способ аппроксимации
Носит название тригонометрической интерполяции. Соотношение (9) называют конечным или дискретным рядом Фурье, а коэффициенты - дискретными коэффициентами Фурье.
Игнорирование установленного нами факта о равенстве функций 
и 
в узлах сетки при 
часто являются источником получения неверных соотношений.
Существует соответствие между задачей приближения функций линейными комбинациями Чебышева и тригонометрическим многочленами. Пусть на отрезке [-1,1] функция f(x) приближается линейными комбинациями 
. Замена переменных x=cost сводит исходную задачу к задаче приближения функции f(cost) линейной комбинацией 
.
Справедливо равенство
.
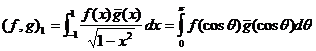Следовательно, задача наилучшего приближения f(x) в норме, соответствующей скалярному произведению 
, эквивалентна задаче приближения 
в норме, соответствующей скалярному произведению 
. Точно так же существует соответствие в случае задач интерполяции и наилучшего приближения в равномерной метрике. Задача интерполирования функции многочленом по узлам 
- нулям многочлена Чебышева 
- после такой замены сводится к задаче интерполирования функции f(cost) при помощи тригонометрического многочлена 
по узлам 
, образующим равномерную сетку.
Похожие работы
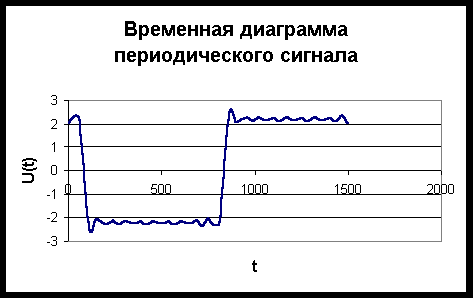
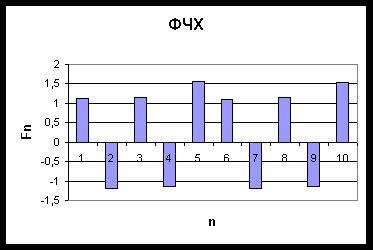
... . Сигнал задан в виде функции времени U(t) , повторяющийся с периодом Т. Требуется выполнить спектральный анализ сигнала и построить графики амплитудного и фазового спектров сигнала. 2.Численные методы расчетов спектральных и временных характеристик периодических сигналов Для расчета спектральных и временных характеристик периодического сигнала используем численные методы, чтобы упростить ...
... , либо функция задана таблично , нахождение интеграла по формуле Ньютона-Лейбница невозможно. Используют приближенные формулы, которые называют квадратурными, либо формулами численного интегрирования. 1) Формулы прямоугольника Пусть y=f(x) непрерывна на [a,b]. Требуется вычислить . Разобьем отрезок интегрирования на n равных частей, точками xi, i=0,n xi=a-i*h шаг ...
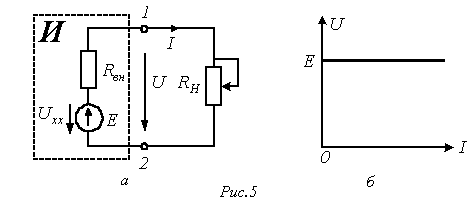
... для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5 Ответ: B= Решить задачу 5, используя соотношения (8) и (9). Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел. Переменный ток долгое время не находил практического ...
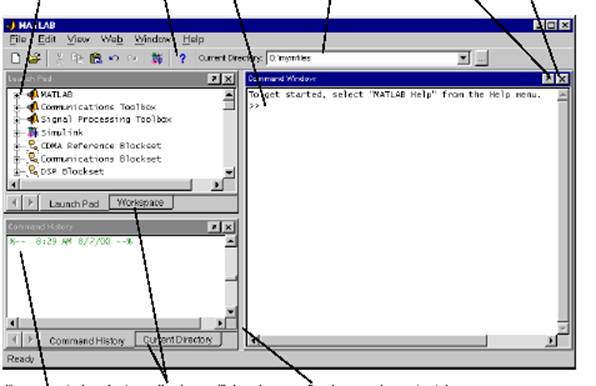
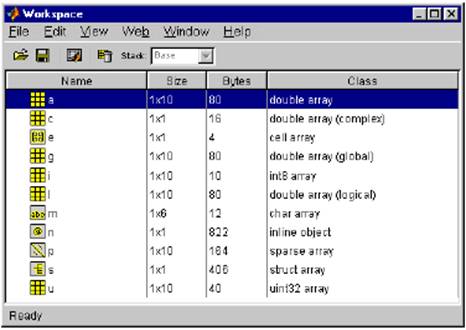
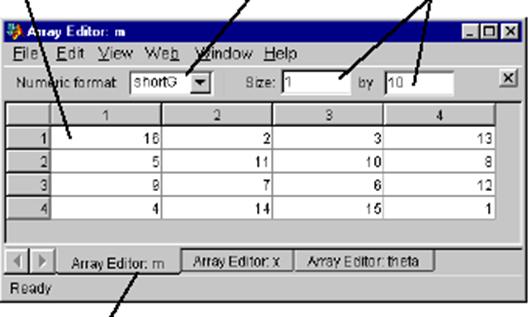
... системам линейных алгебраических уравнений с более чем одной неизвестной; MATLAB решает такие уравнения без вычисле-ния обратной матрицы. Хотя это и не является стандартным математическим обозначением, система MATLAB использует терминологию, связанную с обычным делением в одномерном случае, для описания общего случая решения совместной системы нескольких линейных уравнений. Два символа деления / ...
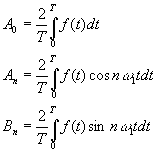
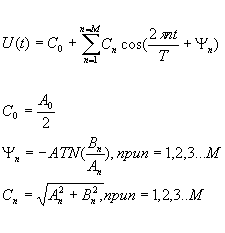
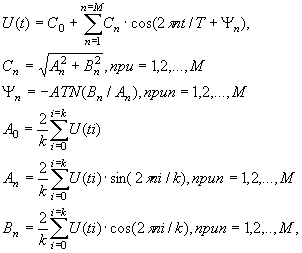
0 комментариев